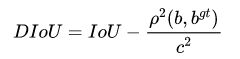GIOU,DIOU

一.IOU 

1.GIOU解决没有交集的框,IOU为0,其损失函数导数为0,无法优化的问题。

图1 GIOU,IOU,l2范数差异

a)可看出 l2值一样,IOU值是不一样的,也就是l2对于尺度不具有不变性

b)可看出当框有包含关系,GIOU就退化为IOU

其是找到一个最小的封闭形状C，让C可以将A和B包围在里面，然后我们计算C中没有覆盖A和B的面积占C总面积的比例S.

GIOU = IOU - S

可看出,GIOU<=IOU

图2 GIOU 计算公式

 

GIOU的损失函数算法:

1.代码 

import numpy as np
def Giou(box1, box2):
    xmin1, ymin1, xmax1, ymax1 = box1
    xmin2, ymin2, xmax2, ymax2 = box2
    xx1 = np.max([xmin1, xmin2])
    yy1 = np.max([ymin1, ymin2])
    xx2 = np.min([xmax1, xmax2])
    yy2 = np.min([ymax1, ymax2])
    # 计算两个矩形框面积
    area1 = (xmax1-xmin1) * (ymax1-ymin1)
    area2 = (xmax2-xmin2) * (ymax2-ymin2)
    inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1]))#计算交集面积
    iou = inter_area / (area1+area2-inter_area+1e-6)#计算交并比
    print('===inter_area:', inter_area)
    print('===iou:', iou)
    #两个框的包围面积
    area_C = (max(xmin1, xmax1, xmin2, xmax2) - min(xmin1, xmax1, xmin2, xmax2)) *\
             (max(ymin1, ymax1, ymin2, ymax2) - min(ymin1, ymax1, ymin2, ymax2))
    print('==area_C:', area_C)
    end_area = (area_C - inter_area) / area_C  #闭包区域中不属于两个框的区域占闭包区域的比重
    giou = iou - end_area
    print('===giou:', giou)
    return giou

box1 = [0, 0, 2, 2]
box2 = [1, 1, 3, 3]
# box2 = [5, 5, 7, 7]
Giou(box1, box2)

二.DIOU

基于IoU和GIoU存在的问题：
1. 直接最小化anchor框与目标框之间的归一化距离是否可行，以达到更快的收敛速度？
2. 如何使回归在与目标框有重叠甚至包含时更准确、更快？

其中,b,bgt分别代表了预测框和真实框的中心点，p2代表计算两个中心点间的欧式距离。 c2代表的是能够同时包含预测框和真实框的最小闭包区域的对角线距离。

DIoU loss可以直接最小化两个目标框的距离，因此比GIoU loss收敛快得多。

1.DIOU代码

import torch
def Diou(bboxes1, bboxes2):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    dious = torch.zeros((rows, cols))
    if rows * cols == 0:#
        return dious
    exchange = False
    if bboxes1.shape[0] > bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        dious = torch.zeros((cols, rows))
        exchange = True
    # #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]
    w1 = bboxes1[:, 2] - bboxes1[:, 0]
    h1 = bboxes1[:, 3] - bboxes1[:, 1]
    w2 = bboxes2[:, 2] - bboxes2[:, 0]
    h2 = bboxes2[:, 3] - bboxes2[:, 1]

    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
    center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
    center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2

    inter_max_xy = torch.min(bboxes1[:, 2:], bboxes2[:, 2:])
    inter_min_xy = torch.max(bboxes1[:, :2], bboxes2[:, :2])
    print('==inter_min_xy:', inter_min_xy)
    print('==inter_max_xy:', inter_max_xy)

    out_max_xy = torch.max(bboxes1[:, 2:], bboxes2[:, 2:])
    out_min_xy = torch.min(bboxes1[:, :2], bboxes2[:, :2])

    print('==out_min_xy:', out_min_xy)
    print('==out_max_xy:', out_max_xy)

    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
    inter_area = inter[:, 0] * inter[:, 1]
    inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
    
    outer = torch.clamp((out_max_xy - out_min_xy), min=0)
    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
    union = area1+area2-inter_area
    dious = inter_area / union - (inter_diag) / outer_diag
    dious = torch.clamp(dious,min=-1.0, max = 1.0)
    if exchange:
        dious = dious.T
    return dious


box1 = torch.from_numpy(np.array([[0, 0, 2, 2]]))
box2 = torch.from_numpy(np.array([[1, 1, 3, 3]]))
Diou(box1, box2)