时频分析之STFT:短时傅里叶变换的原理与代码实现(非调用Matlab API)
1. 引言
在信号分析中,傅里叶变换可称得上是神器。但在实际应用中,人们发现它还是存在一些不可忽视的缺陷。
为了便于叙述考察以下两种情形:
Case 1
考察这样一个函数:
fs = 1000;
t = 0:1/fs:1 - 1/fs;
x = [10 * cos(2 * pi * 10 * t), 20 * cos(2 * pi * 20 * t),...
30 * cos(2 * pi * 30 * t), 40 * cos(2 * pi * 40 * t)];
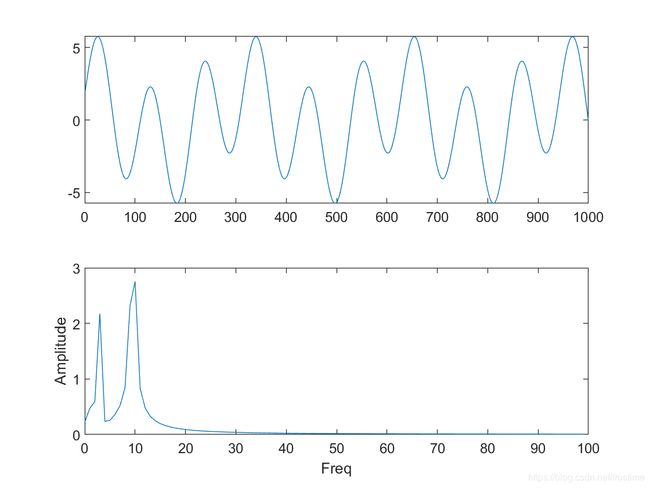
绘制这个函数的时域图像和经过傅立叶变换后的频谱图像,长这个样子:
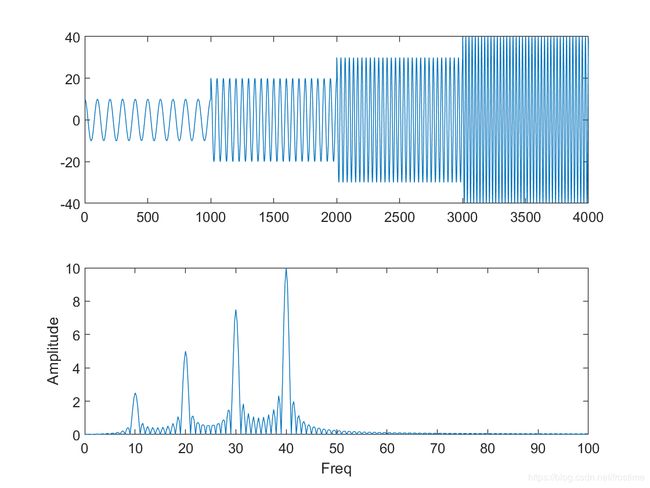
现在把信号反转过来:
x = [10 * cos(2 * pi * 10 * t), 20 * cos(2 * pi * 20 * t),...
30 * cos(2 * pi * 30 * t), 40 * cos(2 * pi * 40 * t)];
x = x(end:-1:1);
再次绘制时域和频域的图像,它长这样:

不难发现,尽管这两个信号的时域分布完全相反,但是它们的频谱图是完全一致的。显然,FFT无法捕捉到信号在时域分布上的不同。
Case 2
考察一个普普通通的信号:
fs = 1000;
t = 0:1/fs:1-1/fs;
x = 2 * cos(2 * 10 * t) + 4 * sin(2 * 30 * t);
现在给信号加入一个高频突变:
sharp = zeros(1, length(x));
% 给信号中间加一个突变
sharp(501:510) = 5 * cos(2 * pi * 100 * linspace(0, 1, 10));
x = x + sharp;
然后绘图:
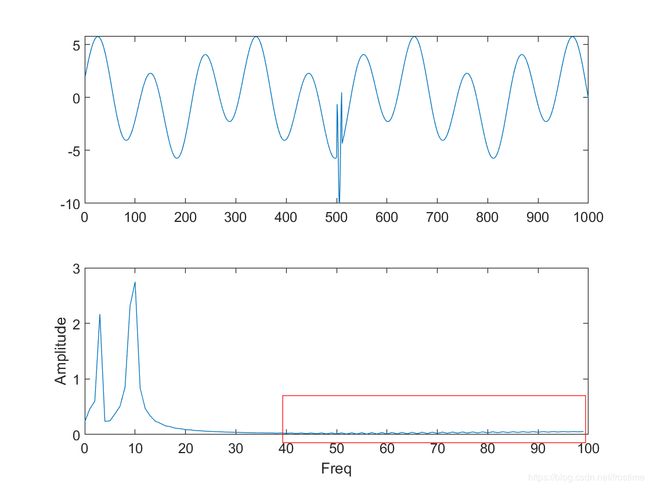
对比两个信号的时域图,我们能很明显发现在第二个信号中央的部分出现了一个突变扰动。然而在频域图中,这样的变化并没有很好的被捕捉到。注意到红框中部分,显然傅里叶变换把突变解释为了一系列低成分的高频信号的叠加,并没有很好的反应突变扰动给信号带来的变化。
为什么我们需要时频分析
通过以上的两个例子,我们不难发现傅立叶变换的缺陷。
第一个例子告诉我们,傅里叶变换只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号,可能频谱图一样。
第二个例子告诉我们,对于信号中的突变,傅里叶变换很难及时捕捉。而在有些场合,这样的突变往往是十分重要的。
当然如果非要硬杠,也不是完全没办法——这就需要需分析相位谱了,但在实际应用中,有谁会不嫌麻烦地去看相位谱呢?
总而言之,傅里叶变换非常擅长分析那些频率特征均一稳定的平稳信号。但是对于非平稳信号,傅立叶变换只能告诉我们信号当中有哪些频率成分——而这对我们来讲显然是不够的。我们还想知道各个成分出现的时间。知道信号频率随时间变化的情况,各个时刻的瞬时频率及其幅值——这也就是时频分析(引用自知乎)。
所谓时频分析,就是既要考虑到频率特征,又要考虑到时间序列变化。常用的有两种方法:短时傅里叶变化,以及小波变换。本文我们只介绍短时傅里叶变换
2. 短时傅里叶变换原理
短时傅里叶变换的思路非常直观:既然对整个序列做FFT会丢失时间信息,那我一段一段地做FFT不就行了嘛!这也正是短时傅里叶变换名称的来源,Short Time Fourier Transorm,这里的 Short Time 就是指对一小段序列做 FFT。
那么怎么一段一段处理呢?直接截取信号的一段来做 FFT 吗?一般我们通过加窗的方法来截取信号的片段。定义一个窗函数 w ( t ) \textrm{w}(t) w(t),比如这样。
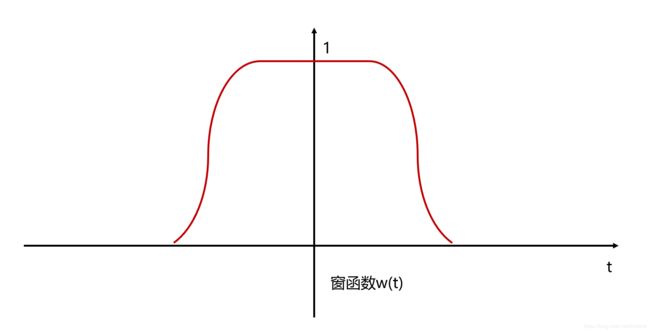
将窗函数位移到某一中心点 τ \tau τ,再将窗函数和原始信号相乘就可以得到截取后的信号 y(t)。
y ( t ) = x ( t ) ⋅ w ( t − τ ) y(t) = x(t) \cdot \textrm{w}(t - \tau) y(t)=x(t)⋅w(t−τ)
前面提到的直接截取的方法其实就是对信号加一个矩形窗,不过一般我们很少选用矩形窗,因为矩形窗简单粗暴的截断方法会产生的频谱泄露以及吉布斯现象,不利于频谱分析。更多关于窗函数的内容,可以看这里:加窗法。
对原始信号 x ( t ) x(t) x(t) 做 STFT 的步骤如下。
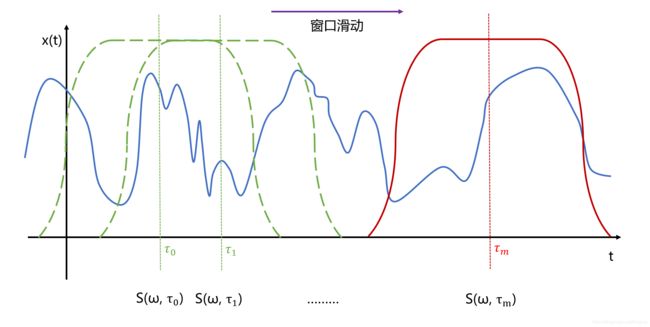
首先将将窗口移动到信号的开端位置,此时窗函数的中心位置在 t = τ 0 t = \tau_0 t=τ0处,对信号加窗处理
y ( t ) = x ( t ) ⋅ w ( t − τ 0 ) y(t) = x(t) \cdot \textrm{w}(t - \tau_0) y(t)=x(t)⋅w(t−τ0)
然后进行傅里叶变换
X ( ω ) = F ( y ( t ) ) = ∫ ∞ + ∞ x ( t ) ⋅ w ( t − τ 0 ) e − j ω t d t X(\omega) = \mathcal{F}(y(t)) = \int_{\infty}^{+\infty}x(t)\cdot \textrm{w}(t-\tau_0) e^{-j\omega t}dt X(ω)=F(y(t))=∫∞+∞x(t)⋅w(t−τ0)e−jωtdt
由此得到第一个分段序列的频谱分布 X ( ω ) X(\omega) X(ω)。在现实应用中,由于信号是离散的点序列,所以我们得到的是频谱序列 X [ N ] X[N] X[N]。
为了便于表示,我们在这里定义函数 S ( ω , τ ) S(\omega, \tau) S(ω,τ),它表示,在窗函数中心为 τ \tau τ 时,对原函数进行变换后的频谱结果 X ( ω ) X(\omega) X(ω),即:
S ( ω , τ ) = F ( x ( t ) ⋅ w ( t − τ ) ) = ∫ ∞ + ∞ x ( t ) ⋅ w ( t − τ ) e − j ω t d t S(\omega, \tau) = \mathcal{F}(x(t)\cdot \textrm{w}(t-\tau)) = \int_{\infty}^{+\infty}x(t)\cdot \textrm{w}(t-\tau) e^{-j\omega t}dt S(ω,τ)=F(x(t)⋅w(t−τ))=∫∞+∞x(t)⋅w(t−τ)e−jωtdt
对应到离散场景中, S [ ω , τ ] S[\omega, \tau] S[ω,τ] 就是一个二维矩阵,每一列代表了在不同位置对信号加窗,对得到的分段进行傅里叶变换后的结果序列。
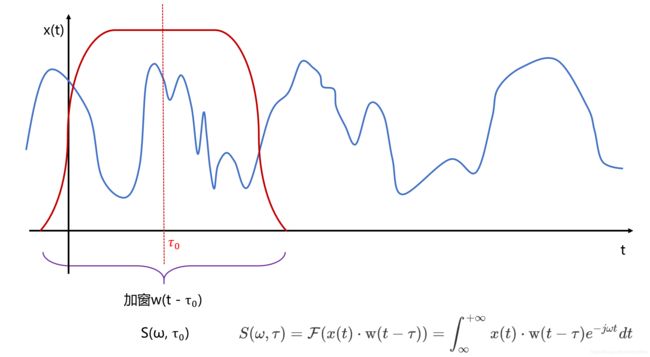
完成了对第一个分段的FFT操作后,移动窗函数到 τ 1 \tau_1 τ1。把窗体移动的距离称为 Hop Size。移动距离一般小于窗口的宽度,从而保证前后两个窗口之间存在一定重叠部分,我们管这个重叠叫 Overlap。
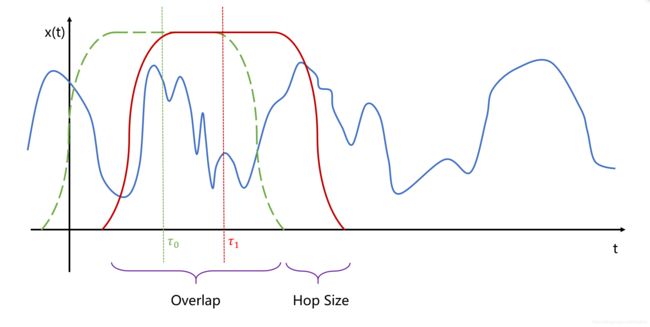
重复以上操作,不断滑动窗口、FFT,最终得到从 τ 0 ∼ τ N \tau_0 \sim \tau_N τ0∼τN 上所有分段的频谱结果:
3. STFT实现
以下代码基于 Matlab 2019b。
3.1 算法实现
STFT 的实现如下,算法返回的三个参数:
- f: m 维向量,表示傅里叶变换后每个点对应的频率值,单位为 Hz
- t: n 维向量,表示 n 个窗口中心时间 τ 1 ∼ τ n \tau_1 \sim \tau_n τ1∼τn,单位为秒
- STFT: 一个二维矩阵 [m, n],每个列向量代表了在对应 τ \tau τ 上 FFT 变换的结果
function [STFT, f, t] = mystft(x, win, hop, nfft, fs)
% 计算短时傅里叶变换
% Input:
% x - 一维信号
% win - 窗函数
% hop - hop size,移动长度
% nfft - FFT points
% fs - 采样率
%
% Output:
% STFT - STFT-矩阵 [T, F]
% f - 频率向量
% t - 时间向量
% 把 x 变为列向量
x = x(:);
xlen = length(x);
wlen = length(win);
% 窗口数目 L
L = 1+fix((xlen-wlen)/hop);
STFT = zeros(nfft, L);
% STFT
for l = 0:L-1
% 加窗
xw = x(1+l*hop : wlen+l*hop).*win;
% FFT计算
X = fft(xw, nfft);
X = fftshift(X);
STFT(:, 1+l) = X(1:nfft);
end
% 取每个窗口中点的时间点
t = (wlen/2:hop:wlen/2+(L-1)*hop)/fs;
%f = (0:nfft-1)*fs/nfft;
% 频率 (fftshift之后的)
f = (-nfft/2:nfft/2-1) * (fs/nfft);
end
3.2 使用范例
我们这里使用 Case 1 的范例来看看 STFT 效果如何。
为了方便可视化,这里给出了对 STFT 变换后的可视化函数。
function PlotSTFT(T,F,S)
% Plots STFT
plotOpts = struct();
plotOpts.isFsnormalized = false;
plotOpts.cblbl = getString(message('signal:dspdata:dspdata:MagnitudedB'));
plotOpts.title = 'Short-time Fourier Transform';
plotOpts.threshold = max(20*log10(abs(S(:))+eps))-60;
signalwavelet.internal.convenienceplot.plotTFR(T,F,20*log10(abs(S)+eps),plotOpts);
end
注意上面这个函数依赖于 signalwavelet 包,如果没有这个依赖的话,我还提供了一个粗糙版的绘图函数,用法基本类似,不过最后一个参数需要把从窗函数对象传进去:
function PlotSTFT_2(T, F, S, win)
wlen = length(win);
C = sum(win)/wlen;
S = abs(S)/wlen/C;
S = 20*log10(S + 1e-6);
%figure(1)
surf(T, F, S)
shading interp;
axis tight;
view(0, 90);
%set(gca, 'FontName', 'Times New Roman', 'FontSize', 14);
xlabel('Time, s');
ylabel('Frequency, Hz');
title('Amplitude spectrogram of the signal');
hcol = colorbar;
%set(hcol, 'FontName', 'Times New Roman', 'FontSize', 14);
ylabel(hcol, 'Magnitude, dB');
end
对 Case 1 中的两种情况进行分析,代码如下
close all; clear; clc;
fs = 1000;
t = 0:1/fs:1 - 1/fs;
% 窗口大小,推荐取 2 的幂次
wlen = 256;
% hop size 即移动步长,一般要取一个小于 wlen 的数,推荐取 2 的幂次
hop = wlen/4;
% FFT 点数,理论上应该不小于wlen,推荐取 2 的幂次
nfft = 256;
x = [10 * cos(2 * pi * 10 * t), 20 * cos(2 * pi * 20 * t),...
30 * cos(2 * pi * 30 * t), 40 * cos(2 * pi * 40 * t)];
figure;
subplot(2, 2, 1);
plot(x);
% 随便选的一个窗函数
win = blackman(wlen, 'periodic');
[S, f, t] = mystft(x, win, hop, nfft, fs);
subplot(2, 2, 2);
PlotSTFT(t,f,S);
x = x(end:-1:1);
subplot(2, 2, 3);
plot(x);
win = blackman(wlen, 'periodic');
[S, f, t] = mystft(x, win, hop, nfft, fs);
subplot(2, 2, 4);
PlotSTFT(t,f,S);
可以看到,在 FFT 中无法区分的频谱图像在 STFT 中区分就非常明显,可以看出按照不同的时间分段,频谱分布的变化。
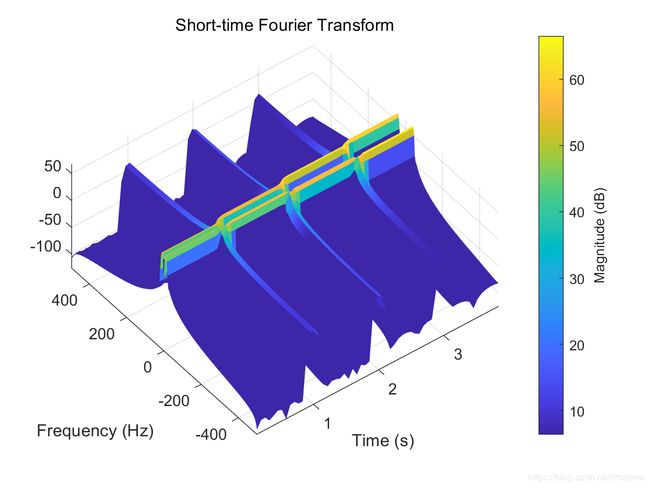
为了更好地理解,将右上角的图做一次三维旋转:
可以非常清晰地看出频率分布随时间的变换。注意到分界线处存在异常的高频成分(就是 STFT 图像中那三条竖线),这是因为时域信号突变导致的高频成分。
3.3 Matlab 中的实现
在老的版本中,Matlab 中 STFT 的函数名为 spectrogram,而在 2019 版本中,引入了新的函数 stft,用法和我上面的实现的程序基本一致。
close all; clear; clc;
fs = 1000;
t = 0:1/fs:1 - 1/fs;
% 窗口大小,推荐取 2 的幂次
wlen = 256;
% hop size 即移动步长,一般要取一个小于 wlen 的数,推荐取 2 的幂次
hop = wlen/4;
% FFT 点数,理论上应该不小于wlen,推荐取 2 的幂次
nfft = 256;
x = [10 * cos(2 * pi * 10 * t), 20 * cos(2 * pi * 20 * t),...
30 * cos(2 * pi * 30 * t), 40 * cos(2 * pi * 40 * t)];
figure;
subplot(1, 3, 1);
win = blackman(wlen, 'periodic');
[S, f, t] = mystft(x, win, hop, nfft, fs);
PlotSTFT(t,f,S);
title('My STFT');
subplot(1, 3, 2);
[S1, f1, t1] = spectrogram(x, win, wlen - hop, nfft, fs);
PlotSTFT(t1, f1, S1);
title('spectrogram');
subplot(1, 3, 3);
[S2, f2, t2] = stft(x, fs, 'Window', win, 'OverlapLength',wlen - hop,'FFTLength',nfft);
PlotSTFT(t2, f2, S2);
title('stft');
需要注意的是,我实现的时候用的参数是 hop size,而matlab提供的函数需要的参数是 overlap 这个别搞混了。结果如下。
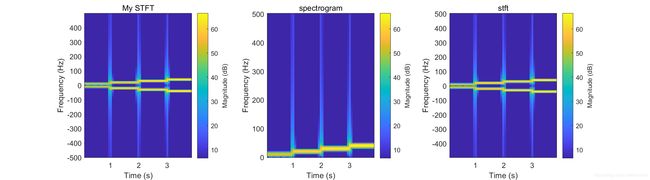
要注意的是,spectrogram 输出的是单边谱,而 stft 输出的是双边谱,其他区别倒不大。但是 spectrogram 还可以输出功率谱,而 stft 就不行了。
4. STFT 的缺点
如果你仔细分析上面的内容,你会发现短时傅立叶变换也有不容忽视的缺陷。
最明显的一个问题:窗口的宽度该设多少为好呢?为了阐明这个问题的影响,我们做这么一个实验:调整不同 wlen 的值,来看看影响。
len = [32, 64, 128, 256];
for i = 1:4
wlen = len(i);
hop = wlen/4;
nfft = wlen;
win = blackman(wlen, 'periodic');
[S, f, t] = mystft(x, win, hop, nfft, fs);
subplot(2, 2, i);
PlotSTFT(t,f,S);
[m, n] = size(S);
t = sprintf('Wlen = %d, S: [%d, %d]', wlen, m, n);
title(t);
end
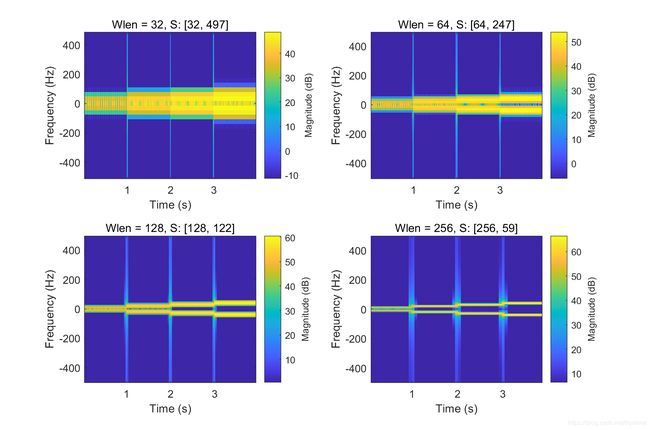
注意 S 的尺寸随 wlen 的变换,不难发现一个事实:
- 窗太窄,窗内的信号太短,会导致频率分析不够精准,频率分辨率差,具体表现是黄色的横线越来越宽、越来越模糊
- 窗太宽,时域上又不够精细,时间分辨率低,具体表现是淡蓝色的竖线越来越宽、越来越模糊(还记得吗,竖线表示交界处的突变造成的高频干扰成分)
从定量的角度来看,STFT的时间分辨率取决于滑移宽度 H H H,而频率分辨率则取决于 F s H \frac{F_s}{H} HFs。显然,一方的增加必然意味着另一方的减小。这就是所谓的时频测不准原理(跟海森堡测不准是一个性质),具体关系为:
Δ t ⋅ Δ f ⩾ 1 4 π \Delta t \cdot \Delta f \geqslant \frac{1}{4\pi} Δt⋅Δf⩾4π1

另外,固定的窗口大小过于死板。对低频信号而言,有可能连一个周期都不能覆盖;对高频信号而言,可能覆盖过多周期,不能反映信号变化。
也就是说,这又是一个 Trade-Off 问题,而一个问题一旦进入 Trade-Off 模式,就开始变得玄学起来了。
为了打破这种玄学困境,就需要一个更加强大的武器——小波变换。
至于小波变换,那就是另一个故事了。