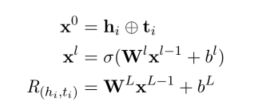元学习——Meta Relational Learning for Few-Shot Link Prediction in Knowledge Graphs（文献解读）

元学习——Meta Relational Learning for Few-Shot Link Prediction in Knowledge Graphs（文献解读）

1. Introduction

常规的知识图谱是由一系列的三元组所组成，三元组的基本形式为：
$$头实体，关系，尾实体$$
尽管在知识图谱中包含了大量的实体、关系和三元组，但是很多的知识图谱仍然是不完整的。因此，知识图谱的完整性是知识图谱发展的一个重要的环节。一类的知识图谱补全的任务是知识图谱的连接预测。其目标是在已经存在的三元组中预测出新的三元组。对于知识图谱的补全任务而言，其基于图谱编码的方式产生了很多的方法，这种思路的核心是学习到隐层的表示，这个过程称为Embedding。Embedding将实体和关系映射到连续的向量空间之中，并且通过编码结果来完成链接预测的任务。

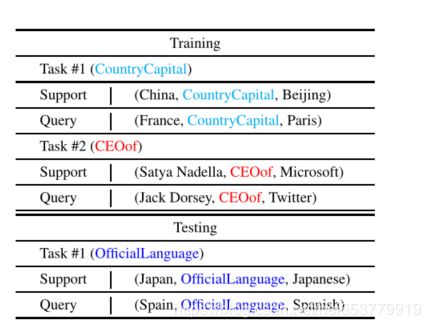
基于编码方式的链接预测，其有效性基于大量的训练样例。如果在训练中样本的数量很少，那么这种方法的结果就会产生很多的错误。然而在实际情况中，小样本的问题在知识图谱中是十分常见的。例如，在维基数据中，大约有10%的关系对应的三元组的数量不超过10个。在本文中，我们的目标是解决知识图谱的小样本的链接预测任务。也就是根据关系对应的K个样本，在给定头实体h和关系r的情况下来预测尾实体t。如下图所示的就是利用K=3的小样本来进行链接预测的任务：

对于知识图谱上的小样本的链接预测任务，其第一次提出的解决方案为GMatching，这种方法的目标是通过考虑一阶的图结构和学习编码方式来得到一个匹配矩阵。在本文中，我们采用的另外一种思路来完成知识图谱的补全任务，我们的思路为：从小样本中传递到不完整的三元组的信息，应该是在一个任务中共享的，普遍的信息。，称这种信息为关系元信息，并且提出了对于解决小样本的链接预测任务的关系元学习的新的学习框架MetaR。同样利用上面的图示，框架将CEOof信息和 CountryCapital通过元关系学习框架从已经存在的小样本传递到不完整的三元组上。

我们定义的关系元信息主要从以下两个方面来帮助我们完成链接预测的任务：

1. 将普遍的关系信息从已经存在的三元组传递到不完整的三元组上。
2. 在一个任务中的小样本来加速学习的过程。

基于上述的两个方面，我们从两个角度来提出两个元信息，包括关系元和梯度元。在我们的框架中，关系元信息比连接头尾实体的一个关系拥有更高的优先级（可以理解为关系元信息是由多个三元组的关系抽象而成）而梯度的元信息是关系元的梯度损失，这种梯度元将在信息从关系元传递到不完整的三元组之前来加速关系元的更新（也就是说，在关系元信息传递到不完整的三元组的时候，已经利用梯度元将关系元更新成一个稳定的信息表示）

相比于GMatching依赖于背景知识图谱，MetaR是独立于这些信息的，所以，相比于基于背景知识图谱信息的方法而言，Meta更加的智能。

总而言之，MetaR在这种小样本的链接预测任务中，主要有以下三种贡献。

1. 文章提出了元关系框架MetaR来完成链接预测任务。
2. 对于小样本的链接预测任务，MetaR对关系元定义了最高的规则。并且提出了两种具体的关系元信息。包括关系元和梯度元。
3. MetR在小样本的链接预测任务上有更好的效果。

2 相关工作

在MetaR模型中，我们的目标是为了学习到能够适应到小样本的链接预测任务的实体的表示。这种学习是受到了知识图谱编码方法的启发。进一步，在MetaR中使用梯度损失是受到了MetaNet和MetaML的启发，这两种方式都是在探索小样本学习的方法。从上述的两个点，我们的相关工作就包括了对于知识图谱编码学习和元学习的调研工作。

2.1 知识图谱编码

知识图谱编码模型是将实体和关系映射到连续的向量空间中，它们使用一种评分函数来检查每一个三元组成立的真实性。与这种知识图谱编码方式类似的是，在MetaR模型中，也采用了一个评分函数，但是和传统的编码方式不同的是，这里使用的关系r是通过MetaR学习到的关系元信息，而不是通过知识图谱编码的过程获得的。

一类评分函数计算的工作是从TransE模型开始的，这是一类使用距离来作为距离来作为评分函数。TransR和TransH也是两种传统的神经网络，并且其使用的是不同的方式来连接头尾实体和它们对应的关系。DisMult和ComplEx是通过RESCAL产生的，其试图采用不同的方式来最小化隐层的语义信息。同样，也有一些方法类似于ConvErt方法，其使用卷积结构来作为三元组的评分函数，并且在模型中添加类似于实体类型的额外信息。

2.2 元学习

元学习的目标是为了对于小样本寻找一个快速学习的能力，并且将这种学习能力泛化到更多的概念中。这种学习的模式接近于人类的学习方式。

目前，有几种元学习的模型被提出。常规的，元学习的三种方式如下：

1. 基于模式匹配的元学习，这种元学习的目标是为了学习到一个在所有任务支持集和查询集中学习到一个匹配模式，这种匹配算法的思路和一些邻近算法类似。其代表算法Siamese Neural Network，GMatching算法等等。
2. 基于模型的元学习，这种元学习的思路是使用了一个类似于“内存”的设计来达到通过少部分的样本来进行快速学习。其代表的算法包括MetaNet等等。
3. 基于优化的元学习，这种元学习的思路是获得更快的优化算法。其代表模型包括MAML算法等等。在MAML算法中，第一步通过一个具体的任务学习器来更新参数，然后优化元通过任务中的更新参数来更新优化器中的参数。

上文中我们提到了，GMatching是第一个用于小样本的链接预测的模型。这种基于匹配的元学习机制考虑邻居的编码，匹配过程以一个LSTM单元来进行实现。

最后，给出元学习对于小样本的的链接预测中的数据的基本形式：

3 任务描述

在这一个章节中，我们提出了对于小样本的知识图谱的链接预测任务的基本定义形式。

首先，一个知识图谱的定义为：

$$G=\{E,R,TP\}$$
其中e表示的实体集合，R表示的是关系集合。而TP表示的为$\{(h,r,t)\in E\ast R\ast E\}$的三元组的集合。

对于任务T，我们定义其小样本的链接预测任务的基本形式：

对于给定的知识图谱G，给定一个支持集$S_r=\{(h_i,t_i)\in E\ast E|(h_i,r,t_i)\in TP\}$，其中关系r∈R，|$S_r$|=K，需要在给定头实体和关系的条件下预测尾实体，其基本的形式如下：
$$r:(h_j,?)$$
这种链接预测称为K样本的链接预测。

通过上面的定义，一个小样本的链接预测任务通常定义在一个具体的关系上。在预测的过程中，通常有超过一个的三元组需要被预测。与支持集$S_r$相对应的是，我们定义一系列的需要被预测三元组，称之为查询集$Q_r=\{r:(h_j,?)\}$

小样本链接预测的最终目标是获取针对一个关系r，通过少量的样本来预测新的三元组的能力。因此其训练的过程是基于一系列的任务$T_{train}=\{T_i{\}}_{i=1}^M$，对于每一个任务而言，其存在$T_i=\{S_i,Q_i\}$。其测试的过程也是对应着一系列的任务$T_{test}=\{T_j{\}}_{j=1}^N$，这种定义和训练过程的定义类似。另外，值得一提的是，测试任务中的关系一定是在训练中出现过。换句话来说，这是一种限定域的链接预测的任务。

注意：这里为了便于书写，译者将论文中的符号变换了一下形式。

4 模型描述

4.1 模型思路

为了是模型能够拥有小样本链接预测的能力，最重要的事情是将公关的信息从支持集传递到查询集中。因此，我们需要考虑一下两个问题：

1. 从支持集传递到查询集中的最重要和最通用的信息是什么？
2. 仅仅通过小的样本集合，如何获得快速学习的能力？

对于以上的两个问题，在一个问题中，在支持集和查询集中的所有的三元组都拥有相同的关系。因此，这里自然的认为在支持集合查询近中最关键的信息是“关系信息”。

对于第二个问题：学习的过程是通过梯度下降来最小化损失实现的，因此梯度反映了模型参数应该如何的进行变换。自然的，我们相信梯度对于加速学习是有效的资源。

基于以上的两个想法，我们在支持集和查询集中提出两种元信息来解决上述的问题。

1. 关系元：表示在支持集和查询集中连接头尾实体的关系信息。并且，我们对于每一个任务抽取关系元信息，对于这种元信息，将其表示为一个向量的形式。
2. 梯度元：其实在支持集中关系元的梯度损失。梯度元展示了关系元应该如何进行变换来达到最小的损失情况。以此来加速学习的过程。关系元通过梯度元进行更新，并且更新的过程是在将信息传递到查询集之前的。

4.2 模型框架

根据上面的两个思路，我们对于整个模型定义为两个部分，分别为：

1. Relation-Meta Learner ：对于关系元学习器，其目标是对在支持集中的头尾实体产生关系元信息。
2. Embedding Learner： 通过实体的编码和关系元来计算包括支持集和查询集中的三元组的真实性，
   基于Embedding Learner的损失函数在关系元被传递到查询集之前来计算和加速更新关系元。

最后，我们给出模型的架构图示：

4.3 关系元学习器

为了从支持集中抽取关系元信息，我们定义一个关系元的学习器来抽取支持集中的头尾实体中的关系信息。关系元学习器可以通过一个简单的神经网络来表示。

在任务$T_r$中，关系元学习器的输入是支持集中的头尾实体，其形式为$\{(h_i,t_i)\in S_r\}$，我们首先通过一个L层的神经网络来抽取实体对的具体的关系信息。，其计算公式如下图所示：

这里，$h_i,t_i$的维度都是d，L表示的神经网络的总的层数，并且$l\in \{1,2,3,4,...,L-1\}$，$W_l,b_l$是l层的权重和偏置项，在实现的时候，论文采用的是LeakyRelu函数来实现激活函数δ。最后，$R(h_i,t_i)$表示的是实体对$h_i,t_i$之间的的具体的关系元信息。

对于多个实体对的关系元信息，我们生成最后的对于该任务的关系元信息，其基本的计算方式为对各个关系元信息求和求平均的过程：
$$R{T}_r=\frac{{\sum }_{i=1}^{K}R(h_i,t_i)}{K}$$

4.4 Embedding Learner

因为我们需要获取到梯度元来加速关系元的更新过程，所以我们需要一个评分函数来对于三元组真实性进行评估，并且我们也需要当前任务的损失结果。

这里我们提出在任务$R{T}_r$评分函数的形式：

$$s(h_j,t_j)=||h_i+R{T}_r-t_i||$$

其中||x||表示的是对于向量X的L2范数。这种评分函数的基本思想来源于TransE模型，其假设的是一个真实的三元组满足$h+r=t$的基本假设。因此这个评分函数定义的是$h+r$和$t$之间的距离。在我们的链接预测中，我们使用关系元信息$R{T}_r$来替代编码获得的关系$r$，$R{T}_r$可以视为任务$T_r$的关系编码。

对于每一个三元组的评分，我们定义以下的损失函数为：

其中$[{]}_{+}$表示的是对于X的正例部分，γ表示的是距离的超参数。其中$s(h_i,t_i^{\prime })$表示的是负例的评分，其对应的真正实体对$(h_i,t_i)\in S_r$，这里$(h_i,r,t_i)\notin G$。

进一步，我们使用$L(S_r)$表示的是模型能够适当的对支持集$S_r$进行编码的损失。因此，其梯度能够指导参数应该如何进行变化。因此，我们$R{T}_r$基于$L(S_r)$的梯作为梯度元$G{T}_r$。
$$G{T}_r={▽}_{R{T}_r}L(S_r)$$
根据上面的梯度，我们定义关系元的更新公式为：
$$R{T}_r^{\prime }=R{T}_r-\beta G{T}_r$$
其中β利用梯度元对关系元进行更新的步长因子。

当基于编码学习器来对查询集中的实体进行评分的时候，我们使用更新之后的关系元。在获取到更新之后的关系元$R^{\prime }$之后，我们将其转移到查询集$Q_r=(h_j,t_j)$中，然后计算其评分和查询集的损失情况，其计算评分和计算损失的公式和支持集中一样。

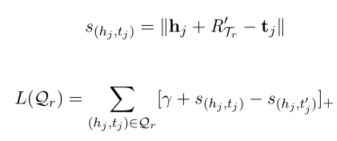
其中$L(Q_r)$是我们的最小化的训练目标。这里我们使用损失来更新整个模型。最后我们定义的训练目标的损失函数为：
$$L=\sum _{(S_r,Q_r)\in T_{train}}L(Q_r)$$

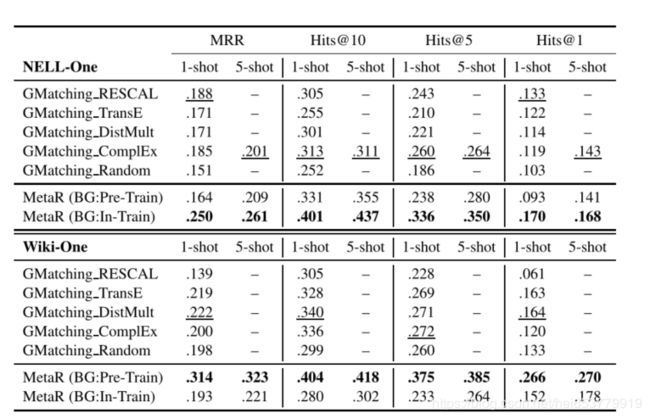
5 实验和结果

6 参考文献

1. Meta Relational Learning for Few-Shot Link Prediction in Knowledge
   Graphs Mingyang Chen 1, Wen Zhang 1, Wei Zhang Qiang Chen Huajun Chen