python-介绍泊松分布(poisson分布)

一、泊松分布问题：

假设我每天接到骚扰电话的次数服从泊松分布，并且经统计平均每天我会接到20个骚扰电话。
请问：
1、我明天接到15个骚扰电话的概率？
2、我明天接到24个骚扰电话以下的概率（包含24）？

二、泊松分布公式：

首先要清楚，泊松分布是离散的，也就是说我接到骚扰电话次数必须是整数，要么就是15次，要么就是16次...,而不会是15.5次。

泊松分布的概率函数为：

累积概率分布函数为：

    

其实就是概率函数的累加。

均值方差：泊松分布的均值和方差都是。

针对上面的问1这里就是20，k就是15。

 

三、解决问题

方法一：根据公式编写代码

import math

def p_possion(k, m):
    kjie = 1  #k!
    for i in range(1, k+1):
        kjie*=i
    pk = math.pow(m, k)/kjie*math.e**(-m)
    return pk

p = p_possion(15, 20)
print("接到15个骚扰电话的概率：",p)

p=0
for i in range(0,25):
    p+=p_possion(i, 20)
print("接到24个骚扰电话以下的概率：",p)

结果：

接到15个骚扰电话的概率： 0.0516488535317584
接到24个骚扰电话以下的概率： 0.8432273781737633

方法二：用scipy包中的scipy.stats.poisson

from scipy import stats

p = stats.poisson.pmf(15, 20)
print("接到15个骚扰电话的概率：",p)

p = stats.poisson.cdf(24, 20)
print("接到24个骚扰电话以下的概率：",p)

四、泊松概率及累积概率分布

仍以骚扰电话为例，计算接到电话0~50次的概率：

from scipy import stats
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']#用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False#用来正常显示负号

X=range(0,51)
Y=[]
for k in X:
    p = stats.poisson.pmf(k, 20)
    Y.append(p)

plt.bar(X, Y, color="red")
plt.xlabel("次数")
plt.ylabel("概率")
plt.title("接到骚扰电话次数及概率")
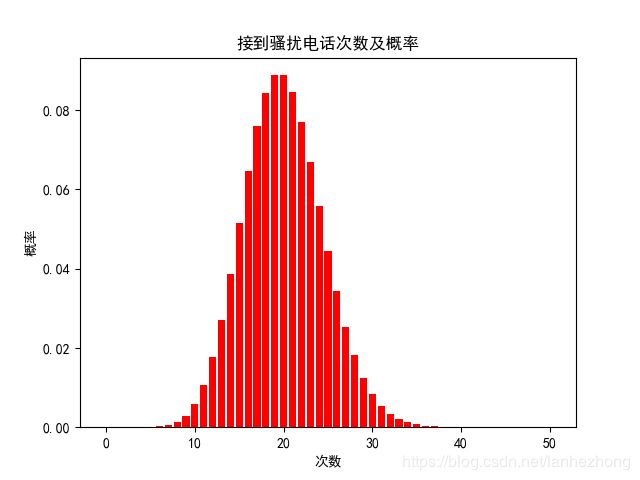
plt.show()

结果：

首先可以看出，在均值20附近，概率最大，均值两边概率呈递减状态。再者可以看到这结果很像二项分布，也像正态分布，关于两者三个分布的相似，这里不做讨论。

五、查表

查表前面代码中有涉及，其实就是查累积概率。查询=100，发生次数小于等于120的概率：

from scipy import stats

p = stats.poisson.cdf(120, 100)
print(p)

结果：0.9773306709216473

六、随机数生成

生成服从=50的泊松分布随机数100个：

from scipy import stats
# 设置random_state时，每次生成的随机数一样。不设置或为None时，多次生成的随机数不一样
sample = stats.poisson.rvs(mu=50, size=100, random_state=3)
print(sample)

结果：

[51 45 60 40 34 53 54 45 45 49 51 46 48 61 47 53 47 48 45 49 52 45 43 50
 50 54 54 47 47 46 36 72 54 55 52 37 42 41 54 54 55 58 53 53 51 43 58 38
 63 50 44 53 48 43 53 45 67 37 51 42 54 47 59 55 54 55 55 46 60 43 54 45
 59 44 58 45 51 58 56 47 54 33 55 50 58 49 60 37 51 43 50 52 52 45 42 44
 49 54 52 48]

 

author：蓝何忠

email：[email protected]