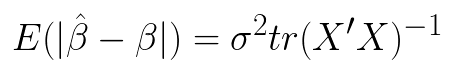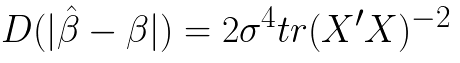SparkML之回归(二)岭回归和Lasso阐述及OLS,梯度下降比较
岭回归（RidgeRegression）
它的上一级称之为Tikhonov regularization，是以Andrey Tikhonov命名的。
Lasso（least absolute shrinkage and selection operator）。两者都
经常用于病态问题的正规化。
在前面部分已经说了，假设我们知道矩阵A和向量b,我们希望找到一个向量x,有：
Ax = b
标准的方法是用OLS，但是当没有满足這样条件的x（比如当x不是满秩情况下），那么就会出现over-fitted 和
under-fitted的问题。岭回归和Lasso就是解决這样的问题。关于岭回归和Lasso的具体内容可以参考文献1.下面
从源码的表达形式，来阐述一些原理。
岭回归（RidgeRegression）在sparkMllib中的表达式如下：
f(weights) = 1/2n ||A weights-y||^2^ + regParam/2 ||weights||^2^
Lasso（least absolute shrinkage and selection operator）在sparkMllib中的表达式如下：
f(weights) = 1/2n ||A weights-y||^2^ + regParam ||weights||_1
可以发现在解决
over-fitted 和
under-fitted這样问题，岭回归（RidgeRegression）是在后面加
regParam/2 ||weights||^2^
Lasso是在后面加 regParam ||weights||_1
也就是在在损失函数：
的后面加上了正则化部分，岭回归（RidgeRegression）是2范数，Lasso是1范数。
对于线性问题，
岭回归（RidgeRegression）和Lasso也被称为L2和L1正规化。根据后面是1范数和2范数来的。
岭回归和Lasso的异同
（1）因为不管是L1还是L2，后面加的都是一个正数，那么就表示，当一些若的特征所对应的系数变为0，所以L2和L1正则
化之后，模型会变成稀疏。（2）岭回归是把系数缩小，而Lasso是把一些系数剔除。但是L2正则化有一个优势，那就是L2正则化会让系数取值变得平均。所以
L2更受人们的青睐。
现在从前面利用普通最小二乘法求多元回归系数开始，下面是回归系数
则
当X有多重共线性是，普通最小二乘估计就变坏，当
时，
变得很大。这时，虽然
是
的无偏估计，但是
时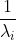，变得很大。这时，虽然是的无偏估计，但是
在具体取值和真实值上存在非常大的差异。那么如果给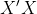
后面加一个
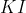,那么就算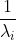，也不会变得很大。这就是达到了解决
over-fitted 這样的问题。那么回归系数就和岭回归参数k,存在如下关系：
后面加一个,那么就算，也不会变得很大。这就是达到了解决
over-fitted 這样的问题。那么回归系数就和岭回归参数k,存在如下关系：
其中K是人们主观决定的，所以k是不唯一的。但又方法确定。
1、岭迹法（缺点：过于主观，令人信服的理论不成套）
定义一系列:岭回归参数K，观看回归系数随岭回归参数K变化情况，有下面一些指标：
（1）回归系数随着岭回归参数K的变化的趋于稳定
（2）用OLS回归的系数，通过岭回归变得正常（在实际应用中，有些系数要为正或负）
（3）MSE趋于稳定
2、GCV（Generalized Gross-Validation）方法
理论可以参考文献2，目的就是让下面GCV最小，此时的K就是最佳的岭回归参数。
利用MATLAB来看看岭回归、Lasso、OLS和梯度下降来看看各个回归系数
数据和代码：链接：http://pan.baidu.com/s/1hshQ3xa 密码：ktlt
load lpsa.data
Y = lpsa(:,1);
X = lpsa(:,2:end);
x1 = X(:,1);
x2 = X(:,2);
x3 = X(:,3);
x4 = X(:,4);
x5 = X(:,5);
x6 = X(:,6);
x7 = X(:,7);
x8 = X(:,8);
%计算矩阵X的相关性
coef = corrcoef(X);
%发现 6，7，8相关性比较强，拿出来分析分析
subplot(1,3,1)
plot(x6,x7,'.')
xlabel('x6'); ylabel('x7'); grid on; axis square
subplot(1,3,2)
plot(x6,x8,'.')
xlabel('x6'); ylabel('x8'); grid on; axis square
subplot(1,3,3)
plot(x7,x8,'.')
xlabel('x7'); ylabel('x8'); grid on; axis square
%% 岭回归
% k :岭回归参数
% b :回归系数
%k = 0:1e-5:5e-3;
k = 0:0.1:1000;
b = ridge(Y,X,k);
figure
plot(k,b,'LineWidth',2)
xlabel('ridge parameters')
ylabel('coefficient ')
title('Ridge regression analysis')
%在1000出感觉有点趋于稳点
ridgeCoef = b(:,1);%此处是随机取一个
%GCV（Generalized Gross-Validation）确定参数
%参考：http://www.stat.washington.edu/courses/stat527/s13/readings/golubetal79.pdf
%% lasso
% B 回归系数
[B,FitInfo] = lasso(X,Y,'CV',10);
lassoPlot(B,FitInfo,'PlotType','CV');
LassoCoef = B(:,1);%此处是随机取一个
%% 普通最小二乘法（ols）
%OLS得到的系数
OLScoef = inv(X'*X)*X'*Y;
%% 梯度下降
% theta 为系数
theta = zeros(8,1);
alpha = 0.1;
y = Y;
m = length(y);
Maxiters = 1000;
for iter = 1:Maxiters
temp1=theta(1)-alpha*(1/m)*(sum((X*theta-y).*X(:,1)));
temp2=theta(2)-alpha*(1/m)*(sum((X*theta-y).*X(:,2)));
temp3=theta(3)-alpha*(1/m)*(sum((X*theta-y).*X(:,3)));
temp4=theta(4)-alpha*(1/m)*(sum((X*theta-y).*X(:,4)));
temp5=theta(5)-alpha*(1/m)*(sum((X*theta-y).*X(:,5)));
temp6=theta(6)-alpha*(1/m)*(sum((X*theta-y).*X(:,6)));
temp7=theta(7)-alpha*(1/m)*(sum((X*theta-y).*X(:,7)));
temp8=theta(8)-alpha*(1/m)*(sum((X*theta-y).*X(:,8)));
theta(1)=temp1;
theta(2)=temp2;
theta(3)=temp3;
theta(4)=temp4;
theta(5)=temp5;
theta(6)=temp6;
theta(7)=temp7;
theta(8)=temp8;
end
%% 系数
% 岭回归得到的系数，正则参数不同，回归系数也不同
% [0.716407012479988;0.292642400760394;-0.142549625985014;0.212007604489450;0.309619533066819;-0.289005615691298;-0.0209135198219117;0.277345952501608]
% lasso回归得到的稀疏，正则参数不同，回归系数也不同
% [0.679207361440420;0.263036185793238;-0.141319231260542;0.210043147964645;0.305019048226535;-0.287867731465690;-0.0208705957688494;0.266362414075235]
% 普通最小二乘法（ols）得到的系数，不会变化
% [0.599895877039271;0.185876494916387;0.280805087089222;0.110759694026575;0.400320416307387;-0.593207551633941;-0.613250168396049;0.916864235688470]
% 梯度下降得到的系数，当收敛时，不会变化，在收敛前，跟学习率、eps、maxiters有关
% [0.599895872830287;0.185876495684477;0.280805086929663;0.110759694108334;0.400320416644753;-0.593207544508389;-0.613250160896409;0.916864226077661]
http://statweb.stanford.edu/~tibs/sta305files/Rudyregularization.pdf
http://www.stat.washington.edu/courses/stat527/s13/readings/golubetal79.pdf
岭回归（RidgeRegression）
它的上一级称之为Tikhonov regularization，是以Andrey Tikhonov命名的。
Lasso（least absolute shrinkage and selection operator）。两者都
经常用于病态问题的正规化。
在前面部分已经说了，假设我们知道矩阵A和向量b,我们希望找到一个向量x,有：
Ax = b
标准的方法是用OLS，但是当没有满足這样条件的x（比如当x不是满秩情况下），那么就会出现over-fitted 和
under-fitted的问题。岭回归和Lasso就是解决這样的问题。关于岭回归和Lasso的具体内容可以参考文献1.下面
从源码的表达形式，来阐述一些原理。
岭回归（RidgeRegression）在sparkMllib中的表达式如下：
f(weights) = 1/2n ||A weights-y||^2^ + regParam/2 ||weights||^2^
Lasso（least absolute shrinkage and selection operator）在sparkMllib中的表达式如下：
f(weights) = 1/2n ||A weights-y||^2^ + regParam ||weights||_1
可以发现在解决
over-fitted 和
under-fitted這样问题，岭回归（RidgeRegression）是在后面加
regParam/2 ||weights||^2^
Lasso是在后面加 regParam ||weights||_1
也就是在在损失函数：
的后面加上了正则化部分，岭回归（RidgeRegression）是2范数，Lasso是1范数。
对于线性问题，
岭回归（RidgeRegression）和Lasso也被称为L2和L1正规化。根据后面是1范数和2范数来的。
岭回归和Lasso的异同
（1）因为不管是L1还是L2，后面加的都是一个正数，那么就表示，当一些若的特征所对应的系数变为0，所以L2和L1正则
化之后，模型会变成稀疏。（2）岭回归是把系数缩小，而Lasso是把一些系数剔除。但是L2正则化有一个优势，那就是L2正则化会让系数取值变得平均。所以
L2更受人们的青睐。
现在从前面利用普通最小二乘法求多元回归系数开始，下面是回归系数
则
当X有多重共线性是，普通最小二乘估计就变坏，当时，变得很大。这时，虽然是的无偏估计，但是
时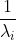，变得很大。这时，虽然是的无偏估计，但是
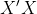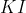在具体取值和真实值上存在非常大的差异。那么如果给后面加一个,那么就算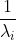，也不会变得很大。这就是达到了解决
over-fitted 這样的问题。那么回归系数就和岭回归参数k,存在如下关系：
后面加一个,那么就算，也不会变得很大。这就是达到了解决
over-fitted 這样的问题。那么回归系数就和岭回归参数k,存在如下关系：
其中K是人们主观决定的，所以k是不唯一的。但又方法确定。
1、岭迹法（缺点：过于主观，令人信服的理论不成套）
定义一系列:岭回归参数K，观看回归系数随岭回归参数K变化情况，有下面一些指标：
（1）回归系数随着岭回归参数K的变化的趋于稳定
（2）用OLS回归的系数，通过岭回归变得正常（在实际应用中，有些系数要为正或负）
（3）MSE趋于稳定
2、GCV（Generalized Gross-Validation）方法
理论可以参考文献2，目的就是让下面GCV最小，此时的K就是最佳的岭回归参数。
利用MATLAB来看看岭回归、Lasso、OLS和梯度下降来看看各个回归系数
数据和代码：链接：http://pan.baidu.com/s/1hshQ3xa 密码：ktlt
load lpsa.data
Y = lpsa(:,1);
X = lpsa(:,2:end);
x1 = X(:,1);
x2 = X(:,2);
x3 = X(:,3);
x4 = X(:,4);
x5 = X(:,5);
x6 = X(:,6);
x7 = X(:,7);
x8 = X(:,8);
%计算矩阵X的相关性
coef = corrcoef(X);
%发现 6，7，8相关性比较强，拿出来分析分析
subplot(1,3,1)
plot(x6,x7,'.')
xlabel('x6'); ylabel('x7'); grid on; axis square
subplot(1,3,2)
plot(x6,x8,'.')
xlabel('x6'); ylabel('x8'); grid on; axis square
subplot(1,3,3)
plot(x7,x8,'.')
xlabel('x7'); ylabel('x8'); grid on; axis square
%% 岭回归
% k :岭回归参数
% b :回归系数
%k = 0:1e-5:5e-3;
k = 0:0.1:1000;
b = ridge(Y,X,k);
figure
plot(k,b,'LineWidth',2)
xlabel('ridge parameters')
ylabel('coefficient ')
title('Ridge regression analysis')
%在1000出感觉有点趋于稳点
ridgeCoef = b(:,1);%此处是随机取一个
%GCV（Generalized Gross-Validation）确定参数
%参考：http://www.stat.washington.edu/courses/stat527/s13/readings/golubetal79.pdf
%% lasso
% B 回归系数
[B,FitInfo] = lasso(X,Y,'CV',10);
lassoPlot(B,FitInfo,'PlotType','CV');
LassoCoef = B(:,1);%此处是随机取一个
%% 普通最小二乘法（ols）
%OLS得到的系数
OLScoef = inv(X'*X)*X'*Y;
%% 梯度下降
% theta 为系数
theta = zeros(8,1);
alpha = 0.1;
y = Y;
m = length(y);
Maxiters = 1000;
for iter = 1:Maxiters
temp1=theta(1)-alpha*(1/m)*(sum((X*theta-y).*X(:,1)));
temp2=theta(2)-alpha*(1/m)*(sum((X*theta-y).*X(:,2)));
temp3=theta(3)-alpha*(1/m)*(sum((X*theta-y).*X(:,3)));
temp4=theta(4)-alpha*(1/m)*(sum((X*theta-y).*X(:,4)));
temp5=theta(5)-alpha*(1/m)*(sum((X*theta-y).*X(:,5)));
temp6=theta(6)-alpha*(1/m)*(sum((X*theta-y).*X(:,6)));
temp7=theta(7)-alpha*(1/m)*(sum((X*theta-y).*X(:,7)));
temp8=theta(8)-alpha*(1/m)*(sum((X*theta-y).*X(:,8)));
theta(1)=temp1;
theta(2)=temp2;
theta(3)=temp3;
theta(4)=temp4;
theta(5)=temp5;
theta(6)=temp6;
theta(7)=temp7;
theta(8)=temp8;
end
%% 系数
% 岭回归得到的系数，正则参数不同，回归系数也不同
% [0.716407012479988;0.292642400760394;-0.142549625985014;0.212007604489450;0.309619533066819;-0.289005615691298;-0.0209135198219117;0.277345952501608]
% lasso回归得到的稀疏，正则参数不同，回归系数也不同
% [0.679207361440420;0.263036185793238;-0.141319231260542;0.210043147964645;0.305019048226535;-0.287867731465690;-0.0208705957688494;0.266362414075235]
% 普通最小二乘法（ols）得到的系数，不会变化
% [0.599895877039271;0.185876494916387;0.280805087089222;0.110759694026575;0.400320416307387;-0.593207551633941;-0.613250168396049;0.916864235688470]
% 梯度下降得到的系数，当收敛时，不会变化，在收敛前，跟学习率、eps、maxiters有关
% [0.599895872830287;0.185876495684477;0.280805086929663;0.110759694108334;0.400320416644753;-0.593207544508389;-0.613250160896409;0.916864226077661]
http://statweb.stanford.edu/~tibs/sta305files/Rudyregularization.pdf
http://www.stat.washington.edu/courses/stat527/s13/readings/golubetal79.pdf