Kalman and Bayesian Filters in Python （卡尔曼与贝叶斯滤波器）笔记

此书从实践角度讲了卡尔曼等一系列贝叶斯滤波器，没有从线控视角入手，提供了大量直观解读和代码实例，看着玩玩摘录些重点

1.g-h滤波器

又称Alpha beta filter，f-g filter，是一类融合观测和估计的滤波器中形式上最朴素的。原书表达不清晰，下为wiki的。g-h滤波器只考虑 x x’ 作为状态变量

其中$x_k$是观测，此算法很简单，（1）（2）按模型更新状态，（3）步融合观测来得到残差，（4）（5）根据残差修订状态。显然其中两个参数是决定的是融合比例。
参数的选择
g的影响

h的影响

2. 离散贝叶斯滤波器

这是卡尔曼滤波，例子滤波等一类滤波器的基本框架

核心思想如下
$$\begin{array}{rlr}\bar{\mathbf{x}}& =\mathbf{x}\ast f_{\mathbf{x}}(\bullet )& \text{Predict Step}\\ \mathbf{x}& =\Vert \mathcal{L}\cdot \bar{\mathbf{x}}\Vert & \text{Update Step}\end{array}$$
$\mathcal{L}$是似然函数。$\Vert \Vert$符号表示取范数。我们需要将概率与先验的乘积标准化以确保$x$是一个和为1的概率分布。
流程伪代码如下：

初始化
初始化我们对状态的信念。
预测
根据系统行为，预测下一步的状态
调整信念，以解释预测中的不确定性
更新
获取测量并给一个对其精度的信念
计算测量值对每个状态匹配的程度（likelihood）
用这种可能性更新状态信念

这种形式的算法有时也叫预测校正。
例子：
背景陈述：假设追踪狗在走廊里的位置，为了方便，离散化为10个位置，其中三个位置由门，其他位置没有。我们对狗的行为一无所知，故采用平坦先验，即认为狗在任意位置出现等可能。不过我们能获得狗身上声呐传感器的数据，故可以知道狗是否在有门的位置。
先看主函数逻辑：

def discrete_bayes_sim(prior, kernel, measurements, z_prob, hallway):
    posterior = np.array([.1]*10)
    priors, posteriors = [], []
    for i, z in enumerate(measurements):
        prior = predict(posterior, 1, kernel)
        priors.append(prior)

        likelihood = lh_hallway(hallway, z, z_prob)
        posterior = update(likelihood, prior)
        posteriors.append(posterior)
    return priors, posteriors
    hallway = np.array([1, 0, 1, 0, 0]*2)
kernel = (.1, .8, .1)
prior = np.array([.1] * 10)
zs = [1, 0, 1, 0, 0, 1]
z_prob = 0.75
priors, posteriors = discrete_bayes_sim(prior, kernel, zs, z_prob, hallway)
interact(animate_discrete_bayes, step=IntSlider(value=12, max=len(zs)*2));

predict函数根据上次位置预测结果为先验进行预测，预测方法是假设其以kernel（）的概率向左或向右移动1个位置。为了计算方便，是通过卷积实现的，是个小trick
convolve(np.roll(pdf, offset), kernel, mode=‘wrap’)
此步骤实际是全概率公式的应用：$$P(X_i^t)=\sum _{j}P(X_j^{t-1})P(x_i|x_j)$$

得到新的prior 后，计算观测的likelihood（对每个点）。
这个玩意在不同具体任务中计算方式不同，本问题中算法很朴素：

  try:
      scale = z_prob / (1. - z_prob)
  except ZeroDivisionError:
      scale = 1e8

  likelihood = np.ones(len(hall))
  likelihood[hall==z] *= scale
  return likelihood

z_prob 表示相信传感器的程度。例子中何为1表示完全相信，故当z=1时强烈加大在三个有门位置的likelihood，z=0时表示一定没门，强烈加大其余位置likelihood。
最后的update步骤实为应用下面的贝叶斯公式产生新息，其将likelihood和prior相乘并归一化
$$p(x_i\mid z)=\frac{p(z\mid x_i)p(x_i)}{p(z)}$$
其中p(x)即prior，p(z|x)即算得的likelihood。分母仅仅是个norm项，顾不必计算，只需归一化一下即可。

最后运行起来如下：

可以看到两件事，一是因为predict的不确定，分布在预测阶段发散，但由于观测的帮助，弥补了纯预测的信度损失。
此方法几大缺陷：
1.此filter是多峰的（multimodal），不能给出唯一确定的答案，不过这在很多场景下反而不是问题
2.需要直接测量状态变化

3.概率，高斯和贝叶斯

俩高斯分布相乘:

$$\begin{array}{rl}\mu & =\frac{{\sigma }_1^2{\mu }_2+{\sigma }_2^2{\mu }_1}{{\sigma }_1^2+{\sigma }_2^2}\\ {\sigma }^2& =\frac{{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}\end{array}$$

俩高斯分布相加

$$\begin{array}{c}\mu ={\mu }_1+{\mu }_2\\ {\sigma }^2={\sigma }_1^2+{\sigma }_2^2\end{array}$$

在前一章的离散分布情形下，我们使用了 element-wise成来updata后验分布，计算比较麻烦，如果分布写作高斯分布形式，即可用上面的公式大大简单计算。

4. 一维卡尔曼滤波

背景问题描述：狗位置预测，传感器返回狗位置，带高斯噪声。
我们以高斯建模传感器观测，套用离散贝叶斯滤波器的基本形式如下

$$\begin{array}{llc}\text{discrete Bayes}& \text{Gaussian}& \text{Step}\\ \bar{\mathbf{x}}=\mathbf{x}\ast f(\mathbf{x})& {\bar{x}}_{\mathcal{N}}=x_{\mathcal{N}}\oplus f_{x_{\mathcal{N}}}(\bullet )& \text{Predict}\\ \mathbf{x}=\Vert \mathcal{L}\bar{\mathbf{x}}\Vert & x_{\mathcal{N}}=L\otimes {\bar{x}}_{\mathcal{N}}& \text{Update}\end{array}$$

具体predict方法
$$\begin{array}{rl}{\bar{x}}_k& =x_{k-1}+v_k\Delta t\\ & =x_{k-1}+f_x\end{array}$$
其中$f_x,x$均为高斯分布。编程上用python的具名数组做了一下，比较规范，还改了repr魔法方法

from collections import namedtuple
gaussian = namedtuple('Gaussian', ['mean', 'var'])
gaussian.__repr__ = lambda s: '?(μ={:.3f}, ?²={:.3f})'.format(s[0], s[1])
'''
g1 = gaussian(3.4, 10.1)
g2 = gaussian(mean=4.5, var=0.2**2)
print(g1)
g1.mean, g1[0], g1[1], g1.var
'''
def predict(pos, movement):
    return gaussian(pos.mean + movement.mean, pos.var + movement.var)

具体update方法
likelihood是给定当前状态下测量的概率，此处likelihood就是我们的measurement，也用高斯表示。
$$\begin{array}{rl}\mathcal{N}(\mu ,{\sigma }^2)& =\Vert prior\cdot likelihood\Vert \\ & =\Vert \mathcal{N}(\bar{\mu },{\bar{\sigma }}^2)\cdot \mathcal{N}({\mu }_z,{\sigma }_z^2)\Vert \\ & =\mathcal{N}(\frac{{\bar{\sigma }}^2{\mu }_z+{\sigma }_z^2\bar{\mu }}{{\bar{\sigma }}^2+{\sigma }_z^2},\frac{{\bar{\sigma }}^2{\sigma }_z^2}{{\bar{\sigma }}^2+{\sigma }_z^2})\end{array}$$

def gaussian_multiply(g1, g2):
    mean = (g1.var * g2.mean + g2.var * g1.mean) / (g1.var + g2.var)
    variance = (g1.var * g2.var) / (g1.var + g2.var)
    return gaussian(mean, variance)

def update(prior, likelihood):
    posterior = gaussian_multiply(likelihood, prior)
    return posterior

人工制造一个观测序列zs，在zs上构建卡尔曼滤波器

# perform Kalman filter on measurement z
for z in zs:    
    prior = predict(x, process_model)
    likelihood = gaussian(z, sensor_var)
    x = update(prior, likelihood)

    kf_internal.print_gh(prior, x, z)

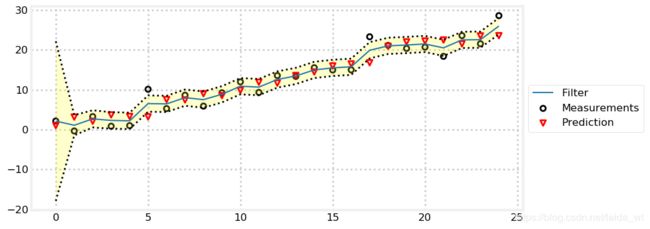
开始方差很大是因为设的初始系统方差很大，可以看到收敛非常快。
以上程序就是一维卡尔曼的实现，下面将其数学表达转换为更传统的表达方式，不过此形式下贝叶斯滤波的意思不再那么明显：
We see that the filter works. Now let’s go back to the math to understand what is happening. The posterior $x$ is computed as the likelihood times the prior ($\mathcal{L}\bar{x}$), where both are Gaussians.

Therefore the mean of the posterior is given by:

$$\mu =\frac{{\bar{\sigma }}^2{\mu }_z+{\sigma }_z^2\bar{\mu }}{{\bar{\sigma }}^2+{\sigma }_z^2}$$

I use the subscript $z$ to denote the measurement. We can rewrite this as:

$$\mu =\left(\frac{{\bar{\sigma }}^2}{{\bar{\sigma }}^2+{\sigma }_z^2}\right){\mu }_z+\left(\frac{{\sigma }_z^2}{{\bar{\sigma }}^2+{\sigma }_z^2}\right)\bar{\mu }$$

In this form it is easy to see that we are scaling the measurement and the prior by weights:

$$\mu =W_1{\mu }_z+W_2\bar{\mu }$$

The weights sum to one because the denominator is a normalization term. We introduce a new term, $K=W_1$, giving us:

$$\begin{array}{rl}\mu & =K{\mu }_z+(1-K)\bar{\mu }\\ & =\bar{\mu }+K({\mu }_z-\bar{\mu })\end{array}$$

where

$$K=\frac{{\bar{\sigma }}^2}{{\bar{\sigma }}^2+{\sigma }_z^2}$$

$K$ is the Kalman gain. It’s the crux of the Kalman filter. It is a scaling term that chooses a value partway between ${\mu }_z$ and $\bar{\mu }$.

Let’s work a few examples. If the measurement is nine times more accurate than the prior, then ${\bar{\sigma }}^2=9{\sigma }_z^2$, and

$$\begin{array}{rl}\mu & =\frac{9{\sigma }_z^2{\mu }_z+{\sigma }_z^2\bar{\mu }}{9{\sigma }_z^2+{\sigma }_{\mathtt{z}}^2}\\ & =\left(\frac{9}{10}\right){\mu }_z+\left(\frac{1}{10}\right)\bar{\mu }\end{array}$$

Hence $K=\frac{9}{10}$, and to form the posterior we take nine tenths of the measurement and one tenth of the prior.

If the measurement and prior are equally accurate, then ${\bar{\sigma }}^2={\sigma }_z^2$ and

$$\begin{array}{c}\mu =\frac{{\sigma }_z^2(\bar{\mu }+{\mu }_z)}{2{\sigma }_{\mathtt{z}}^2}\\ =\left(\frac{1}{2}\right)\bar{\mu }+\left(\frac{1}{2}\right){\mu }_z\end{array}$$

which is the average of the two means. It makes intuitive sense to take the average of two equally accurate values.

We can also express the variance in terms of the Kalman gain:

$$\begin{array}{rl}{\sigma }^2& =\frac{{\bar{\sigma }}^2{\sigma }_z^2}{{\bar{\sigma }}^2+{\sigma }_z^2}\\ & =K{\sigma }_z^2\\ & =(1-K){\bar{\sigma }}^2\end{array}$$

按此推导的等价实现如下：

def update(prior, measurement):
    x, P = prior        # mean and variance of prior
    z, R = measurement  # mean and variance of measurement
    
    y = z - x        # residual
    K = P / (P + R)  # Kalman gain

    x = x + K*y      # posterior
    P = (1 - K) * P  # posterior variance
    return gaussian(x, P)

def predict(posterior, movement):
    x, P = posterior # mean and variance of posterior
    dx, Q = movement # mean and variance of movement
    x = x + dx
    P = P + Q
    return gaussian(x, P)

总结：

Predict

$\begin{array}{lll}\text{Equation}& \text{Implementation}& \text{Kalman Form}\\ \bar{x}=x+f_x& \bar{\mu }=\mu +{\mu }_{f_x}& \bar{x}=x+dx\\ & {\bar{\sigma }}^2={\sigma }^2+{\sigma }_{f_x}^2& \bar{P}=P+Q\end{array}$

Update

$\begin{array}{lll}\text{Equation}& \text{Implementation}& \text{Kalman Form}\\ x=\Vert \mathcal{L}\bar{x}\Vert & y=z-\bar{\mu }& y=z-\bar{x}\\ & K=\frac{{\bar{\sigma }}^2}{{\bar{\sigma }}^2+{\sigma }_z^2}& K=\frac{\bar{P}}{\bar{P}+R}\\ & \mu =\bar{\mu }+Ky& x=\bar{x}+Ky\\ & {\sigma }^2=\frac{{\bar{\sigma }}^2{\sigma }_z^2}{{\bar{\sigma }}^2+{\sigma }_z^2}& P=(1-K)\bar{P}\end{array}$

其他小问题：
1.此方法难以处理非线性
2.在面临受限的硬件时，可以直接将K设为其最后的收敛值来简化计算。

5.多维高斯

$$f(\mathbf{x},\mu ,\Sigma )=\frac{1}{\sqrt{(2\pi {)}^n|\Sigma |}}\exp [-\frac{1}{2}(\mathbf{x}-\mu {)}^{\mathsf{T}}{\Sigma }^{-1}(\mathbf{x}-\mu )]$$
由于其协方差矩阵包含变量关系的信息，因此对预测是有帮助的
多维高斯相乘：
$$\begin{array}{rl}\mu & ={\Sigma }_2({\Sigma }_1+{\Sigma }_2{)}^{-1}{\mu }_1+{\Sigma }_1({\Sigma }_1+{\Sigma }_2{)}^{-1}{\mu }_2\\ \Sigma & ={\Sigma }_1({\Sigma }_1+{\Sigma }_2{)}^{-1}{\Sigma }_2\end{array}$$

6.多维卡尔曼滤波

算法：

Predict

$\begin{array}{lll}\text{Univariate}& \text{Univariate}& \text{Multivariate}\\ & \text{(Kalman form)}& \\ \bar{\mu }=\mu +{\mu }_{f_x}& \bar{x}=x+dx& \bar{\mathbf{x}}=\mathbf{F}\mathbf{x}+\mathbf{B}\mathbf{u}\\ {\bar{\sigma }}^2={\sigma }_x^2+{\sigma }_{f_x}^2& \bar{P}=P+Q& \bar{\mathbf{P}}={\mathbf{F}\mathbf{P}\mathbf{F}}^{\mathsf{T}}+\mathbf{Q}\end{array}$

$\mathbf{x},\mathbf{P}$ 是状态均值和方差

$\mathbf{F}$ 是状态转移矩阵

$\mathbf{Q}$ 过程方差

$\mathbf{B}$ ， $\mathbf{u}$ 输入矩阵和输入，新加入的

Update

$\begin{array}{lll}\text{Univariate}& \text{Univariate}& \text{Multivariate}\\ & \text{(Kalman form)}& \\ & y=z-\bar{x}& \mathbf{y}=\mathbf{z}-\mathbf{H}\bar{\mathbf{x}}\\ & K=\frac{\bar{P}}{\bar{P}+R}& \mathbf{K}={\bar{\mathbf{P}}\mathbf{H}}^{\mathsf{T}}({\mathbf{H}\bar{\mathbf{P}}\mathbf{H}}^{\mathsf{T}}+\mathbf{R}{)}^{-1}\\ \mu =\frac{{\bar{\sigma }}^2{\mu }_z+{\sigma }_z^2\bar{\mu }}{{\bar{\sigma }}^2+{\sigma }_z^2}& x=\bar{x}+Ky& \mathbf{x}=\bar{\mathbf{x}}+\mathbf{K}\mathbf{y}\\ {\sigma }^2=\frac{{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}& P=(1-K)\bar{P}& \mathbf{P}=(\mathbf{I}-\mathbf{K}\mathbf{H})\bar{\mathbf{P}}\end{array}$

$\mathbf{H}$ 观测函数

$\mathbf{z},\mathbf{R}$ 是测量均值和测量方差

$\mathbf{y}$ ， $\mathbf{K}$ 残差，卡尔曼增益

与单变量相比，只是引入了矩阵，其他都一样：

• 使用高斯函数来表示我们对状态和误差的估计
• 使用高斯函数表示测量值及其误差
• 使用高斯函数表示过程模型
• 使用过程模型预测下一个状态(先验)
• 在测量值和先验值之间形成一个估计
  注：细节的一些直观理解
  在predict步中，状态方差以$\bar{\mathbf{P}}={\mathbf{F}\mathbf{P}\mathbf{F}}^{\mathsf{T}}+\mathbf{Q}$方式计算得到，而不是简单P+Q，这是因为要映射到相同空间才能运算。${\mathbf{F}\mathbf{P}\mathbf{F}}^{\mathsf{T}}$将P从t-1状态空间映射变换到t的状态空间。

下面以之前的狗追踪问题举例说明
这次试用位置和速度作为状态变量，其中位置可测，作为观测变量，速度作为隐变量，假设做匀速直线运动，并估测了初试位置和过程方差，如下，过程方差Q还未确定

from filterpy.kalman import predict

x = np.array([10.0, 4.5])
P = np.diag([500, 49])
F = np.array([[1, dt], [0, 1]])

# Q is the process noise
x, P = predict(x=x, P=P, F=F, Q=0)

预测结果如下：

可以看到随着 predict的进行，不确定在增加，同时速度与位置的相关性在增加。
过程噪声设计：
Q是表示系统受外界的干扰的，具体细节在下章讨论，现在先使用库函数计算

from filterpy.common import Q_discrete_white_noise
Q = Q_discrete_white_noise(dim=2, dt=1., var=2.35)
print(Q)
'''
[[0.588 1.175]
 [1.175 2.35 ]]
 '''

最后，我们加上控制项，这可以让我们得以控制对象。$\Delta \mathbf{x}=\mathbf{B}\mathbf{u}$，至此，完整的预测方程已经确定，次例子是无控的，故设u=0$$\bar{\mathbf{x}}=\mathbf{F}\mathbf{x}+\mathbf{B}\mathbf{u}$$
之后来看updata步：
为了求观测和预测之间的残差，需要一个观测函数（矩阵）H将状态空间映射到观测空间。本例中为[1,0]，最后设置好观测方差R，整个滤波器就完全确定好了

from filterpy.kalman import update
H = np.array([[1., 0.]])
R = np.array([[5.]])
z = 1.
x, P = update(x, P, z, R, H)

7. 卡尔曼滤波器数学细节

动态系统的状态空间表达
一般建立系统微分方程后很容易得到连续状态方程$\dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u}+w$（w是噪声），接下来的问题是要离散化为${\mathbf{x}}_k={\mathbf{F}\mathbf{x}}_{k-1}$以让计算机得以运行。离散化实际上就是在解微分方程组，方法很多，工程上常用数值方法。如van Loan’s方法可求 ${\mathbf{F}}_k$ 并同时得到 ${\mathbf{Q}}_k$
过程噪声Q的确定
相似的，我们也需要对噪声w离散化以确定Q，具体要看我们对噪声的假设，典型的有连续白噪声模型和分段白噪声模型，各有利弊，实践上通过实验来确定。其具体计算可调用如下：

from filterpy.common import Q_continuous_white_noise
from filterpy.common import Q_discrete_white_noise

Q = Q_continuous_white_noise(dim=2, dt=1, spectral_density=1)
Q = Q_discrete_white_noise(2, var=1.)

Q可以被简化。当时间步t很小的时候，我们大可以只保留最高阶状态变量对应的值，而将其他设为0。如
$$\mathbf{Q}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& {\sigma }^2\end{array}\right]$$
对 $x={\left[\begin{array}{cccccc}x& \dot{x}& \ddot{x}& y& \dot{y}& \ddot{y}\end{array}\right]}^{\mathsf{T}}$ Q 将为 6x6，这时可以保留$\ddot{x}$ ， $\ddot{y}$ ，其他都设为0.

$\mathbf{P}=(\mathbf{I}-\mathbf{K}\mathbf{H})\bar{\mathbf{P}}$的计算稳定性问题
由于浮点数的精度损失，此式子在计算的时候可能使得P不再对称，由于P是协方差矩阵，其应该是严格对称的，这会导致滤波器发散等一系列错误。因此实际上使用了Joseph 方程计算P。$$\mathbf{P}=(\mathbf{I}-\mathbf{K}\mathbf{H})\bar{\mathbf{P}}(\mathbf{I}-\mathbf{K}\mathbf{H}{)}^{\mathsf{T}}+{\mathbf{K}\mathbf{R}\mathbf{K}}^{\mathsf{T}}$$
此方法不仅能解决因为浮点不对称引起的滤波器不稳定，亦可一定程度上解决因模型不精确和非高斯噪声等实际环境引起的滤波器发散问题。

8.面向实际问题的卡尔曼滤波器的设计

以过滤来自有噪声传感器的(x,y)为例（人工数据，匀速直线运动）。显然可取状态变量和转移矩阵
$$\mathbf{x}={\left[\begin{array}{cccc}x& \dot{x}& y& \dot{y}\end{array}\right]}^{\mathsf{T}}$$
$$\left[\begin{array}{c}x\\ \dot{x}\\ y\\ \dot{y}\end{array}\right]=\left[\begin{array}{cccc}1& \Delta t& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& \Delta t\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ \dot{x}\\ y\\ \dot{y}\end{array}\right]$$
之后设计过程噪声，采用离散白噪声模型，并认为x,y直接独立。
系统无控制，故设B=0。
确定观测矩阵：由于我们传感器返回${\left[\begin{array}{cc}x& y\end{array}\right]}^{\mathsf{T}}$ ，且单位为英尺，故设:
$$\mathbf{H}=\left[\begin{array}{cccc}\frac{1}{0.3048}& 0& 0& 0\\ 0& 0& \frac{1}{0.3048}& 0\end{array}\right]$$
观测噪声矩阵：认为x,y独立，假设高斯噪声，设：
$$\mathbf{R}=\left[\begin{array}{cc}{\sigma }_x^2& {\sigma }_y{\sigma }_x\\ {\sigma }_x{\sigma }_y& {\sigma }_y^2\end{array}\right]=\left[\begin{array}{cc}5& 0\\ 0& 5\end{array}\right]$$
最后设置下初始值，注意P初值习惯上给的较大。
$$\mathbf{x}=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right],\mathbf{P}=\left[\begin{array}{cccc}500& 0& 0& 0\\ 0& 500& 0& 0\\ 0& 0& 500& 0\\ 0& 0& 0& 500\end{array}\right]$$

from filterpy.stats import plot_covariance_ellipse
from kf_book.book_plots import plot_filter

R_std = 0.35
Q_std = 0.04

def tracker1():
    tracker = KalmanFilter(dim_x=4, dim_z=2)
    dt = 1.0   # time step

    tracker.F = np.array([[1, dt, 0,  0],
                          [0,  1, 0,  0],
                          [0,  0, 1, dt],
                          [0,  0, 0,  1]])
    tracker.u = 0.
    tracker.H = np.array([[1/0.3048, 0, 0, 0],
                          [0, 0, 1/0.3048, 0]])

    tracker.R = np.eye(2) * R_std**2
    q = Q_discrete_white_noise(dim=2, dt=dt, var=Q_std**2)
    tracker.Q = block_diag(q, q)
    tracker.x = np.array([[0, 0, 0, 0]]).T
    tracker.P = np.eye(4) * 500.
    return tracker

# simulate robot movement
N = 30
sensor = PosSensor((0, 0), (2, .2), noise_std=R_std)

zs = np.array([sensor.read() for _ in range(N)])

# run filter
robot_tracker = tracker1()
mu, cov, _, _ = robot_tracker.batch_filter(zs)

for x, P in zip(mu, cov):
    # covariance of x and y
    cov = np.array([[P[0, 0], P[2, 0]], 
                    [P[0, 2], P[2, 2]]])
    mean = (x[0, 0], x[2, 0])
    plot_covariance_ellipse(mean, cov=cov, fc='g', std=3, alpha=0.5)
    
#plot results
zs *= .3048 # convert to meters
plot_filter(mu[:, 0], mu[:, 2])
plot_measurements(zs[:, 0], zs[:, 1])
plt.legend(loc=2)
plt.xlim(0, 20);                     
                                                          

效果尚可

模型阶数选择
具体应该用多少阶的模型来描述实际问题？下面给出0,1,2阶的系统，并对其进行性能分析。具体分析方法是画出真实值与预测值直接的残差，并借助P矩阵的对角线画出置信域，如下是一阶的：

当换到二阶滤波器，虽然短期内不是很差，但可观察到长期发散。

高阶数的过程模型很容易过拟合，我们可以选择采用较低阶数，同时适当加大过程噪声Q以达到统样不错的效果。
检测和避免糟糕的测量值
显然实践中由于传感器故障等原因我们偶尔会得到很糟糕的观测值，这个需要被检测和剔除以避免其破坏性影响。一个朴素但有效的做法是gating。可以利用P矩阵中的状态方差来判断观测值的好坏。具体的，可以使用mahalanobis distance。mahalanobis distance判断一个点到分布的距离，其定义如下：
$$D_m=\sqrt{(\mathbf{x}-\mu {)}^{\mathsf{T}}{\mathbf{S}}^{-1}(\mathbf{x}-\mu )}$$
其中S是协方差矩阵。
它其实很像欧氏距离:
$$D_e=\sqrt{(\mathbf{x}-\mathbf{y}{)}^{\mathsf{T}}(\mathbf{x}-\mathbf{y})}$$
若S是对角阵，马氏距离可简化为：
$$D_m=\sqrt{\sum _{i-1}^N\frac{(x_i-{\mu }_i{)}^2}{{\sigma }_i}}$$
就是欧氏距离加了个方差做因子。
滤波器性能评估
真实环境下的卡尔曼滤波器设计往往靠式，因此这里提几个滤波器性能的客观量化指标。

1. Normalized Estimated Error Squared（NEES）
   这是当能获取状态变量ground-truth时的最佳选择。
   $$\begin{gathered} \tilde{\mathbf{x}}=\mathbf{x}-\hat{\mathbf{x}} \\ ϵ={\tilde{\mathbf{x}}}^{\mathsf{T}}{\mathbf{P}}^{-1}\tilde{\mathbf{x}} \end{gathered}$$

from filterpy.stats import NEES

事实上这是一个假设检验方法。我们认定当NEES的均值<状态变量维度时是一个好的滤波器。
2. 似然函数
当无法获得ground-truth的时候，可计算似然，即观测符合当前模型假设的程度。
$$\begin{array}{rl}\mathbf{y}& =\mathbf{z}-\mathbf{H}\bar{\mathbf{x}}\\ \mathbf{S}& ={\mathbf{H}\bar{\mathbf{P}}\mathbf{H}}^{\mathsf{T}}+\mathbf{R}\\ \mathcal{L}=\frac{1}{\sqrt{2\pi S}}\exp [-\frac{1}{2}{\mathbf{y}}^{\mathsf{T}}{\mathbf{S}}^{-1}\mathbf{y}]& \end{array}$$
这个也很适合用于剔除坏的测量，如下

9.非线性滤波

原始的卡尔曼滤波器是线性的，我们生活在非线性的世界，需要一些非线性的技术。
非线性
数学上的线性要求以下两点：

• additivity: $f(x+y)=f(x)+f(y)$
• homogeneity: $f(ax)=af(x)$

非线性的效果
考虑一个有噪声雷达跟踪系统，它向我们报告物体距离50km，方位90度，那么我们直觉上可能认为其绝对坐标应该是（50，0）。我们设距离方差为0.4，角度方差为0.35，并采样3000点如下，计算3000点的均值标记为星。

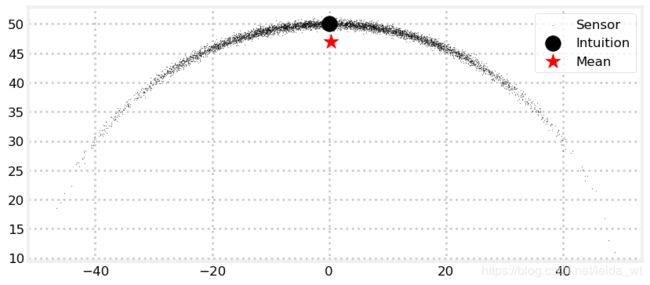
可见由于非线性的缘故，我们的直觉失效了。
下图绘出了分析函数对高斯分布的影响，可以看到虽然f(x)看起来还是挺线性的，但是影响巨大，这对卡尔曼滤波器的假设具有破坏性打击。

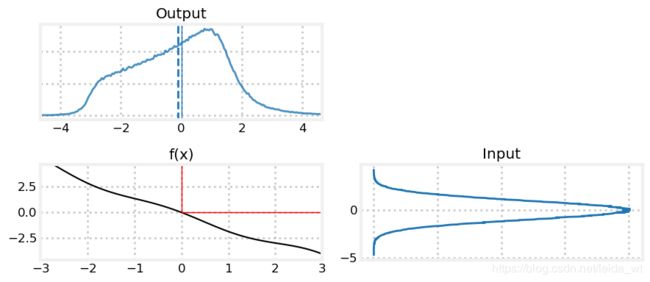
UKF,EKF,例子滤波 是几种处理非线性滤波的有效手段，尤其UKF和粒子滤波器在实践中取得了非常好的效果。

9. 无迹卡尔曼滤波器UKF

该技术与1997年提出，相对于EKF等算是比较新的。有趣的是其名称中的unscented一词并没有任何含义，而是源于发明者开的玩笑。。。
上一章的例子使我们了解到由于非线性函数的存在，新状态已经难以解析的计算得到，因此需要引入采样方法进行数值求解。单纯使用大量随机采样（蒙特卡洛思路）是最朴素的方法，效果不错，能很好的近似原分布经过非线性函数后的均值和方差，但考虑到这个采样在每个时间步update中都要进行，计算量实在太大。更好的方法是使用加权采样。选择的采样点称之为sigma points，记为$\mathbf{\chi }$。当我们通过一些采样方法得到$\mathbf{\chi }$后，并可进行如下的计算
$$\mathcal{Y}=f(\mathbf{\chi })$$
将$\mathbf{\chi }$通过非线性函数计算其对应的映射之后，计算均值和方差作为新的估计，拿到这些估计值后我们便可与标准的线性卡尔曼滤波方法接轨了。故UKF方法的精髓就是以加权采样近似估计状态在非线性变换之后的均值方差，借助于较好的采样算法，这个估计一般是不错的，故此方法可以在非线性系统中取得较好的性能。
具体算法
$$\begin{array}{ll}\text{Kalman Filter}& \text{Unscented Kalman Filter}\\ & \mathcal{Y}=f(\mathbf{\chi })\\ \bar{\mathbf{x}}=\mathbf{F}\mathbf{x}& \bar{\mathbf{x}}=\sum w^m\mathcal{Y}\\ \bar{\mathbf{P}}={\mathbf{F}\mathbf{P}\mathbf{F}}^{\mathsf{T}}+\mathbf{Q}& \bar{\mathbf{P}}=\sum w^c(\mathcal{Y}-\bar{\mathbf{x}})(\mathcal{Y}-\bar{\mathbf{x}}{)}^{\mathsf{T}}+\mathbf{Q}\\ & \mathcal{Z}=h(\mathcal{Y})\\ & {\mathbf{\mu }}_z=\sum w^m\mathcal{Z}\\ \mathbf{y}=\mathbf{z}-\mathbf{H}\mathbf{x}& \mathbf{y}=\mathbf{z}-{\mathbf{\mu }}_z\\ \mathbf{S}={\mathbf{H}\bar{\mathbf{P}}\mathbf{H}}^{\mathsf{T}}+\mathbf{R}& {\mathbf{P}}_z=\sum w^c(\mathcal{Z}-{\mathbf{\mu }}_z)(\mathcal{Z}-{\mathbf{\mu }}_z{)}^{\mathsf{T}}+\mathbf{R}\\ \mathbf{K}={\bar{\mathbf{P}}\mathbf{H}}^{\mathsf{T}}{\mathbf{S}}^{-1}& \mathbf{K}=\left[\sum w^c(\mathcal{Y}-\bar{\mathbf{x}})(\mathcal{Z}-{\mathbf{\mu }}_z{)}^{\mathsf{T}}\right]{\mathbf{P}}_z^{-1}\\ \mathbf{x}=\bar{\mathbf{x}}+\mathbf{K}\mathbf{y}& \mathbf{x}=\bar{\mathbf{x}}+\mathbf{K}\mathbf{y}\\ \mathbf{P}=(\mathbf{I}-\mathbf{K}\mathbf{H})\bar{\mathbf{P}}& \mathbf{P}=\bar{\mathbf{P}}-\mathbf{K}{\mathbf{P}}_{\mathbf{z}}{\mathbf{K}}^{\mathsf{T}}\end{array}$$
可以看到仅是进行一些调整，其他完全符合卡尔曼滤波的思想。
首先，由于非线性系统难以用状态方程描述，这里转而使用非线性函数$f$描述$F$。相应的，观测矩阵$H$也替换为了$h$函数。$w^m,w^c$分别是sigma points的均值权重和方差权重，在构造sigma points时生成。
Sigma Point的采样方法
几十年来大家水了很多采样方法，目前大家用的最多的是Van der Merwe的方法，其能很好的平衡计算复杂度和精度。该方法由$\alpha$, $\beta$, $\kappa$三个参数控制。
为了方便我们记$\lambda ={\alpha }^2(n+\kappa )-n$
先看点的位置如何得到：
首先一个特殊的采样点是
$${\mathcal{X}}_0=\mu$$
之后其余点的计算
$${\mathbf{\chi }}_i=\{\begin{array}{ll}\mu +{\left[\sqrt{(n+\lambda )\Sigma }\right]}_i& \text{for i=1 .. n}\\ \mu -{\left[\sqrt{(n+\lambda )\Sigma }\right]}_{i-n}& \text{for i=(n+1) .. 2n}\end{array}$$
其中n是状态向量x的维数，$\Sigma$是协方差矩阵P。±的形式保证了对称性。下标$i$表示取矩阵的第$i$列。此式子通俗理解是以$\mu$为中心，扩散$\Sigma$的一个系数大小的的值。这里的矩阵开方是个很神奇的东西，其定义不唯一，此处使用如下定义：若$\Sigma ={\mathbf{S}\mathbf{S}}^{\mathsf{T}}$则 $S=\sqrt{\Sigma }$。具体的，使用$\mathbf{S}=\text{cholesky}(\mathbf{P})$ 作为$\mathbf{P}$的开方。其中cholesky是cholesky分解。
之后看权重的计算：
$$\begin{gathered} W_0^m=\frac{\lambda }{n+\lambda } \\ {W}_0^c=\frac{\lambda }{n+\lambda }+1-{\alpha }^2+\beta \\ {W}_i^m=W_i^c=\frac{1}{2(n+\lambda )}i=1..2n \end{gathered}$$
此方法的采样结形如下图：

至于三个参数的选择，可如下进行：
$\beta =2$ is a good choice for Gaussian problems, $\kappa =3-n$ where $n$ is the dimension of $\mathbf{x}$ is a good choice for $\kappa$, and $0\le \alpha \le 1$ is an appropriate choice for $\alpha$, where a larger value for $\alpha$ spreads the sigma points further from the mean.
一个例子：航班追踪

此任务的目标是由雷达给出的距离和角度的观测，得到（x，y）。
我们采用匀速直线运动假设：
$$\mathbf{x}=\left[\begin{array}{c}\mathtt{d}\mathtt{i}\mathtt{s}\mathtt{t}\mathtt{a}\mathtt{n}\mathtt{c}\mathtt{e}\\ \mathtt{v}\mathtt{e}\mathtt{l}\mathtt{o}\mathtt{c}\mathtt{i}\mathtt{t}\mathtt{y}\\ \mathtt{a}\mathtt{l}\mathtt{t}\mathtt{i}\mathtt{t}\mathtt{u}\mathtt{d}\mathtt{e}\end{array}\right]=\left[\begin{array}{c}x\\ \dot{x}\\ y\end{array}\right]$$
显然转移矩阵是线性的：
$$\bar{\mathbf{x}}=\left[\begin{array}{ccc}1& \Delta t& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ \dot{x}\\ y\end{array}\right]$$
但本例中的观测函数就是非线性的了：
$$\text{r}=\sqrt{(x_{\text{ac}}-x_{\text{radar}}{)}^2+(y_{\text{ac}}-y_{\mathtt{r}\mathtt{a}\mathtt{d}\mathtt{a}\mathtt{r}}{)}^2}$$

$$ϵ={\tan }^{-1}\frac{y_{\mathtt{a}\mathtt{c}}-y_{\text{radar}}}{x_{\text{ac}}-x_{\text{radar}}}$$
代码实现如下：
首先创造仿真环境：飞机和雷达站

from numpy.linalg import norm
from math import atan2

class RadarStation(object):
    
    def __init__(self, pos, range_std, elev_angle_std):
        self.pos = np.asarray(pos)       
        self.range_std = range_std
        self.elev_angle_std = elev_angle_std

    
    def reading_of(self, ac_pos):
        """ Returns (range, elevation angle) to aircraft. 
        Elevation angle is in radians.
        """
        
        diff = np.subtract(ac_pos, self.pos)
        rng = norm(diff)
        brg = atan2(diff[1], diff[0])
        return rng, brg


    def noisy_reading(self, ac_pos):
        """ Compute range and elevation angle to aircraft with 
        simulated noise"""
        
        rng, brg = self.reading_of(ac_pos)      
        rng += randn() * self.range_std
        brg += randn() * self.elev_angle_std 
        return rng, brg       

class ACSim(object):   
    def __init__(self, pos, vel, vel_std):
        self.pos = np.asarray(pos, dtype=float)
        self.vel = np.asarray(vel, dtype=float)
        self.vel_std = vel_std        
        
    def update(self, dt):
        """ Compute and returns next position. Incorporates 
        random variation in velocity. """
        
        dx = self.vel*dt + (randn() * self.vel_std) * dt      
        self.pos += dx     
        return self.pos

之后便可实现借助filterpy库实现UKF：

def f_radar(x, dt):
    """ state transition function for a constant velocity 
    aircraft with state vector [x, velocity, altitude]'"""
    
    F = np.array([[1, dt, 0],
                  [0,  1, 0],
                  [0,  0, 1]], dtype=float)
    return np.dot(F, x)
def h_radar(x):
    dx = x[0] - h_radar.radar_pos[0]
    dy = x[2] - h_radar.radar_pos[1]
    slant_range = math.sqrt(dx**2 + dy**2)
    elevation_angle = math.atan2(dy, dx)
    return [slant_range, elevation_angle]
import math
from kf_book.ukf_internal import plot_radar

dt = 3. # 12 seconds between readings
range_std = 5 # meters
elevation_angle_std = math.radians(0.5)
ac_pos = (0., 1000.)
ac_vel = (100., 0.)
radar_pos = (0., 0.)
h_radar.radar_pos = radar_pos

points = MerweScaledSigmaPoints(n=3, alpha=.1, beta=2., kappa=0.)
kf = UKF(3, 2, dt, fx=f_radar, hx=h_radar, points=points)

kf.Q[0:2, 0:2] = Q_discrete_white_noise(2, dt=dt, var=0.1)
kf.Q[2,2] = 0.1

kf.R = np.diag([range_std**2, elevation_angle_std**2])
kf.x = np.array([0., 90., 1100.])
kf.P = np.diag([300**2, 30**2, 150**2])

np.random.seed(200)
pos = (0, 0)
radar = RadarStation(pos, range_std, elevation_angle_std)
ac = ACSim(ac_pos, (100, 0), 0.02)

time = np.arange(0, 360 + dt, dt)
xs = []
for _ in time:
    ac.update(dt)
    r = radar.noisy_reading(ac.pos)
    kf.predict()
    kf.update([r[0], r[1]]) 
    xs.append(kf.x)   
plot_radar(xs, time)    

最后，呈现一个较复杂的例子
此例子处理机器人定位问题。我们有一个机器人，它需要用传感器感知地标来定位和导航。
机器人模型采用经典的自行车模型来建模。
$$\begin{array}{rl}\bar{x}& =x-R\sin (\theta )+R\sin (\theta +\beta )\\ \bar{y}& =y+R\cos (\theta )-R\cos (\theta +\beta )\\ \bar{\theta }& =\theta +\beta \end{array}$$
其中$\beta =\frac{d}{w}\tan (\alpha )$ ，$R=\frac{d}{\beta }$
选定状态变量$\mathbf{x}={\left[\begin{array}{ccc}x& y& \theta \end{array}\right]}^{\mathsf{T}}$
选定控制变量$\mathbf{u}={\left[\begin{array}{cc}v& \alpha \end{array}\right]}^{\mathsf{T}}$（α是前轮转向角）
明确地标p的观测函数：
$$\begin{array}{rlr}\mathbf{z}& =h(\mathbf{x},\mathbf{P})& +\mathcal{N}(0,R)\\ & =\left[\begin{array}{c}\sqrt{(p_x-x{)}^2+(p_y-y{)}^2}\\ {\tan }^{-1}(\frac{p_y-y}{p_x-x})-\theta \end{array}\right]& +\mathcal{N}(0,R)\end{array}$$
这里需要小心角度相减的计算问题，即0°附近的离散性，显然可以取模处理之。
此外还需要注意的是如何对角度求平均？显然359°和1°的平均是0°，但其数值均值却为180°。因此我们需要特别考虑此问题，使用下面的式子计算角度均值：
$$\bar{\theta }=atan2\left(\frac{{\sum }_{i=1}^n\sin {\theta }_i}{n},\frac{{\sum }_{i=1}^n\cos {\theta }_i}{n}\right)$$
规定的这些均值计算方法可以传入UKF类的初始化函数。
具体代码见原书，不赘述，具有很好参考价值。
实验：
给一组手工设定的控制序列，撒一些地标，运行如下。可以看到不确定度很小。

删去一些地标，误差显著增大。

11. 扩展卡尔曼滤波器EKF

EKF算法在卡尔曼发表线性卡尔曼滤波器后很快被提出，其应对非线性的能力相对较差，同时理论比较繁琐，故暂略

12. 粒子滤波器PF

之前的技术不能处理多目标，强非线性，强非高斯噪声，无过程模型的场景，这些场景下可以使用PF。
粒子滤波器是一类滤波器，通用的粒子滤波算法框架如下：

1. 随机产生一群粒子
   粒子可以有位置、方向 和/或 任何其他需要估计的状态变量。
   每一个粒子都有一个权值(概率)，表示它与系统实际状态匹配的可能性。
   用相同的权重初始化每个对象。

2. 预测粒子的下一个状态
   根据你对真实系统行为的预测来移动粒子。

3. 更新
   根据测量结果更新颗粒的权重。
   与测量值紧密相称的粒子的权重要高于与测量值不匹配的粒子。

4. 重采样
   抛弃非常不可能的粒子，用更可能的粒子的拷贝替换它们。

5. 计算估计
   （可选）计算一组粒子的加权平均值和协方差，得到状态估计。

以车辆追踪问题为例，我们选定（x,y,θ）为粒子的变量
初始化阶段，随机初始化粒子状态，基于1/N的均等权重
预测阶段我们让例子有噪声地按控制变量移动
更新阶段我们计算每个例子对观测的似然度，以似然度更新例子权重
重采样阶段我们按例子权重随机采样，防止退化。具体操作方法如下：
对归一化权重[0.0625, 0.125 , 0.1875, 0.25 , 0.125 , 0.1875, 0.0625]，计算累积和序列得[0.0625, 0.1875, 0.375 , 0.625 , 0.75 , 0.9375, 1. ]以便画出如下的图。之后制造0-1的随机数，按照几何概型，其落在各个色块的概率就是权重，进行N次后就可达到完整的重采样结果。

重采样不是每次更新都进行的，没有新息注入时重采样并无意义。我们使用一下指标决定何时进行重采样：
$${\hat{N}}_{\text{eff}}=\frac{1}{\sum w^2}$$（w是粒子权重）
重采样在此值小于每一给定的阈值（比如N/2，其中N为粒子数）后进行。此值是对当前有用粒子数量的估计。这种策略称Sampling Importance Resampling (SIR)。

在上面的预测和更新两步中我们按输入u移动例子，并使用观测更新其对应权重，这种方法的理论依据正是著名的重要性采样（统计学通用方法，也被openai用在PPO中用于构建off-policy learning）：
使用重要性采样可以更换采样分布，将无法计算的
$$\mathbb{E}[f(x)]=\int f(x)\pi (x)dx$$
转为
$$\mathbb{E}[f(x)]=\int f(x)q(x)\cdot \frac{\pi (x)}{q(x)}dx$$
在上面的机器人追踪问题中，分布π即机器人状态的分布，这是不一定对的（因为是推断的结果），而q分布即新获得的测量的分布，可以认为是准确的。因此自然的利用重要性采样公式换到q上采样会得到更精准的值。在具体实施中，我们计算的是$\mu =\sum _{i=1}^N{x}^i{w}^i$，即加权平均，其中权重w就是重要性采样公式中的π/q。
粒子滤波中不同的重采样方法
重采样在粒子滤波中起到防止粒子退化的作用，有重要意义。除了上面的采样方法，还有残差重采样（Residual Resampling），分层重采样（Stratified Resampling），系统重采样（Systematic Resampling）。作者认为其中比较好的是系统重采样，这在采样量小的时候比较明显（所谓好指采样结果符合权重的程度好坏，好的采样应该很好符合权重规定的比例关系），但个人感觉在点稍多的时候这并不是个问题。不过系统重采样有O(N)的复杂度，这比上面的O(Nlog(N))好。
总结
在线性和高斯噪声的假设下，卡尔曼滤波是最优估计，而粒子滤波则可处理非线性和无模型系统，不需要高斯和线性假设。但是粒子滤波的性能分析，稳定性分析都很困难，计算量也大，不过这也是处理和非线性有关问题时经常见到的。KF，UKF，EKF已经在工业上获得了很多实时在线应用的机会。随着计算成本的不断下降，未来粒子滤波类可能也会有不错的应用。

13. 平滑器

卡尔曼滤波器是在线滤波方法，之利用历史信息，而对于离线滤波场景，使用平滑器可扩展到使用整个序列信息进行滤波，效果会更好。
固定区间平滑（Fixed-Interval Smoothing）
这类平滑器在接受到一个完整的区间后一并进行估计操作。RTS是这类中最主要的方法。RTS先运行标准卡尔曼滤波，得到所有的估计值X和对应系统协方差P。之后用X和P，按下面算法从第K步预测到第1步（即反向预测）：
预测：
$$\begin{array}{rl}\mathbf{P}& ={\mathbf{F}\mathbf{P}}_k{\mathbf{F}}^{\mathsf{T}}+\mathbf{Q}\end{array}$$
更新：
$$\begin{array}{rl}{\mathbf{K}}_k& ={\mathbf{P}}_k{\mathbf{F}}^{\mathsf{T}}{\mathbf{P}}^{-1}\\ {\mathbf{x}}_k& ={\mathbf{x}}_k+{\mathbf{K}}_k({\mathbf{x}}_{k+1}-{\mathbf{F}\mathbf{x}}_k)\\ {\mathbf{P}}_k& ={\mathbf{P}}_k+{\mathbf{K}}_k({\mathbf{P}}_{k+1}-\mathbf{P}){\mathbf{K}}_k^{\mathsf{T}}\end{array}$$
效果显著：

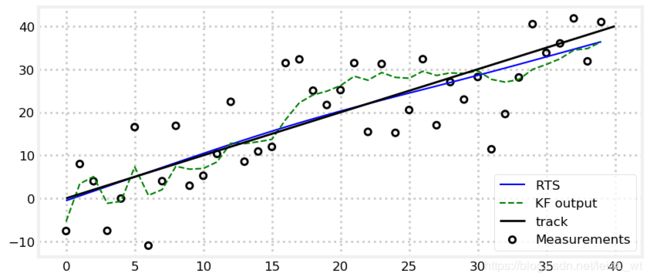
14. 自适应滤波

Adaptive Filtering旨在处理模型不匹配的情况，其检查到有当前过程模型无法描述的动态行为时可以自适应的调整。（回想在之前非自适应的滤波器中，我们只能增大Q以权衡模型的问题，但大的Q会使我们的滤波器不再进行最优估计）
我们建立一个ManeuveringTarget类来产生人工数据。ManeuveringTarget模拟了二维平面的小车，可以接受转向和加减速指令。另外设计个模拟传感器，吐出加噪声后的（x，y）。给一个转向的数据实例如下：

下面我们尝试以匀速直线运动模型的卡尔曼滤波器对齐进行滤波，为方便起见只做x坐标。结果如下，可见由于转向导致的与模型不符，有了很大的估计误差，不过误差在观测的纠正下逐渐变小：

为了解决这个，我们可以大幅加大Q，但这也导致了估计质量的下降：

或，我们可以增大模型阶数，改为横加速度直线运动模型，同样可以有效解决滞后的问题，但依旧顾此失彼，估计噪声明显大了：

因此，若我们能设计一种机制动态的改变滤波器模型，比如在恒速运动阶段使用低阶模型降低噪声，在转向等阶段使用高阶模型保证响应则有望较好的平衡矛盾。
我们可以观察滤波器里的残差来得知目标运动状态何时发生变化，如下：

自适应思路1：可调过程噪声
第一种方法是使用低阶模型，并根据机动是否发生来调整过程噪声。当残差变得“大”时，我们将增加过程噪声。这将导致滤波器更倾向于测量而不是过程预测，并且滤波器将密切跟踪信号。当残差很小时，我们将缩小过程噪声。
一种连续调整的方法计算残差的归一化值$ϵ={{\mathbf{y}}^{\mathsf{T}}\mathbf{S}}^{-1}\mathbf{y}$，其中S是过程噪声：$\mathbf{S}=\mathbf{H}\mathbf{P}{\mathbf{H}}^{\mathsf{T}}+\mathbf{R}$。我们可以设一个${ϵ}_{max}$（可通过实验选择，一个不错的经验值是$ϵ$ 的4~5倍标准差），当$ϵ>{ϵ}_{max}$时将Q矩阵成一个扩大系数$q_{factor}$即可。下图${ϵ}_{max}=4，q_{factor}=1000$，可见显著的性能提升。

此外，还可计算$std=\sqrt{{\mathbf{H}\mathbf{P}\mathbf{H}}^{\mathsf{T}}+\mathbf{R}}$ 之后采用如下策略改变Q：当残差>std的某一倍数时，增大Q
自适应思路2：渐消记忆滤波器（Fading memory filters）
此类方法优势不被归类为自适应滤波方法。此方法的关注点在卡尔曼滤波器的记忆性上。标准卡尔曼滤波使用了1~k-1的所有信息，但这可能导致过大的“惯性”，我们加入一个微小的修改，将原方法中$\bar{\mathbf{P}}={\mathbf{F}\mathbf{P}\mathbf{F}}^{\mathsf{T}}+\mathbf{Q}$更改为$\tilde{\mathbf{P}}={\alpha }^2{\mathbf{F}\mathbf{P}\mathbf{F}}^{\mathsf{T}}+\mathbf{Q}$。其中α>1，但通常很接近1，比如1.02。这样做的考虑是若我们增加估计误差协方差，滤波器对估计的不确定性就会增加，因此它给测量增加了权重，从而减小了滤波器的惯性。此法的改动微乎其微，实现很方便，值得一试，虽然效果不是很惊艳。

自适应思路3：多模型估计
这是一种集成（ensemble ）的思路。最朴素的想法是搞一把模型，然后看情况切换，当然也可进行UKF,KF的集成或对不同的状态变量使用不同的模型或算法。
我们很容易实现的方法是对残差进行阈值判断，以此来切换模型，但这种硬切换显然会导致估计结果不连续的跳跃。因此，我们采用多模型自适应估计技术（MMAE），该方法按模型likelihoods给出融合结果。其中似然函数已在前述章节有过讨论：$\mathcal{L}=\frac{1}{\sqrt{2\pi S}}\exp [-\frac{1}{2}{\mathbf{y}}^{\mathsf{T}}{\mathbf{S}}^{-1}\mathbf{y}]$，其中y是残差，S是系统不确定性。之后按$p_k^i=\frac{{\mathcal{L}}_k^i{p}_{k-1}^i}{\sum _{j=1}^N{\mathcal{L}}_k^j{p}_{k-1}^j}$分配即可。此方法的一个缺陷是算法可能收敛到只信任某一最可能算法上去，这需要被注意，可以通过重新初始化选择权重进行修正。

此外还有交互式多模型技术 IMM（Interacting Multiple Model），利用贝叶斯方法在多个模型间转移，但为了交互，其要求模型必需有相同的维数，这是个比较大的限制。

完。