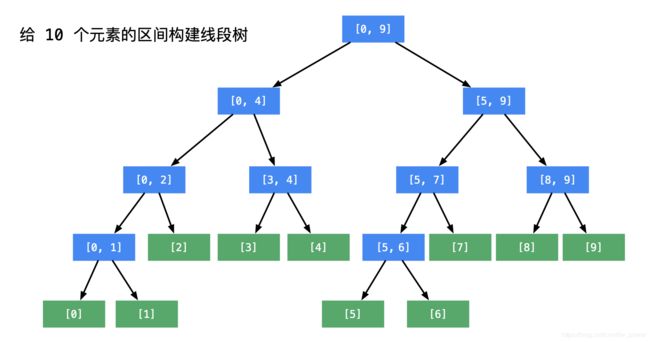
「线段树」第 2 节：写出预处理数组的结构

由于「线段树」是平衡二叉树，因此可以使用数组表示

• 以前我们学习过「堆」，知道「堆」是一棵「完全二叉树」，因此「堆」可以用数组表示。基于此，我们很自然地想到可以用数组表示「线段树」；
• 完全二叉树的定义：除了最后一层以外，其余各层的结点数达到最大，并且最后一层所有的结点都连续地、集中地存储在最左边；
• 线段树虽然不是完全二叉树，但线段树是平衡二叉树，依然也可以用数组表示。

如何构建线段树、如何实现区间查询、如何实现区间更新

「自顶向下」递归构建线段树

• 首先看看「线段树」长什么样；
• 线段树是一种二叉树结构，不过在实现的时候，可以使用数组实现，这一点和「优先队列」、「并查集」是一致的。

当区间里结点的个数恰好是 $2$ 的方幂时：

需要多少空间

• 「线段树」的一个经典实现是从上到下递归构建，这一点很像根据员工人数来定领导的人数，设置多少领导的个数就要看员工有多少人了；
• 再想一想，我们在开篇对于线段树的介绍，线段树适合支持的操作是「查询」和「更新」，不适用于「添加」和「删除」。

下面以「员工和领导」为例，讲解从上到下逐步构建线段树的步骤：我们首先要解决的问题是「一共要设置多少领导」，我们宁可有一些位置没有人坐，也要让所有的人都坐下，因此我们在做估计的时候只会放大。

线段树是一颗平衡二叉树

比较极端的一种情况：

比较一般的一种情况：

• 线段树是一棵二叉树，除了最后一层以外，每一层都是「满」的；
• 第 $i$ 层（$i$ 从 0 开始计算）的结点个数为 $2^i$；
• 第 $i$ 层 之前的所有结点的个数之和：$$2^0+2^1+2^2+\cdots +2^{i-1}=\frac{1\times (1-2^i)}{1-2}=2^i-1<2^i$$
• 假设 $N=2^i$，最坏情况下，还要占用下一层，使用 $2N$ 空间，第 $i$ 层 之前的所有结点的个数之和小于 $N$；
• 所以 $$N+N+2N=4N$$这么多空间肯定够了。

根据上面的讨论，我们可以写出线段树的代码框架：

Java 代码：

public class SegmentTree<E> {
    // 一共要给领导和员工准备的椅子，是我们要构建的辅助数据结构
    private E[] tree;
    // 原始的领导和员工数据，这是一个副本
    private E[] data;

    public SegmentTree(E[] arr) {
        this.data = data;
        // 数组初始化
        data = (E[]) new Object[arr.length];
        for (int i = 0; i < arr.length; i++) {
            data[i] = arr[i];
        }
        tree = (E[]) new Object[4 * arr.length];
    }

    public int getSize() {
        return data.length;
    }

    public E get(int index) {
        if (index < 0 || index >= data.length) {
            throw new IllegalArgumentException("Index is illegal.");
        }
        return data[index];
    }

    /**
     * 返回完全二叉树的数组表示中，索引所表示的元素的左孩子结点的索引
     * 注意：索引编号从 0 开始
     *
     * @param 线段树的某个结点的索引
     * @return 传入的结点的左结点的索引
     */
    public int leftChild(int index) {
        return 2 * index + 1;
    }

    /**
     * 返回完全二叉树的数组表示中，索引所表示的元素的左孩子结点的索引
     * 注意：索引编号从 0 开始
     *
     * @param 线段树的某个结点的索引
     * @return 传入的结点的右结点的索引
     */
    public int rightChild(int index) {
        return 2 * index + 2;
    }

}

Python 代码：

class SegmentTree:

    def __init__(self, arr):
        self.data = arr
        # 开 4 倍大小的空间
        self.tree = [None for _ in range(4 * len(arr))]

    def get_size(self):
        return len(self.data)

    def get(self, index):
        if index < 0 or index >= len(self.data):
            raise Exception("Index is illegal.")
        return self.data[index]

    def __left_child(self, index):
        return 2 * index + 1

    def __right_child(self, index):
        return 2 * index + 2

「力扣」第 303 题：区域和检索 - 数组不可变

• 题目链接：303. 区域和检索 - 数组不可变

方法：基于线段树（区间树）的实现。

Java 代码：

public class NumArray {

    private SegmentTree<Integer> segmentTree;

    public NumArray(int[] nums) {
        // 把数组传给线段树
        if(nums.length>0){
            Integer[] data = new Integer[nums.length];
            for (int i = 0; i < nums.length; i++) {
                data[i] = nums[i];
            }
            segmentTree = new SegmentTree<>(data, (a, b) -> a + b);
        }
    }

    public int sumRange(int i, int j) {
        if(segmentTree==null){
            throw new IllegalArgumentException("Segment Tree is null");
        }
        return segmentTree.query(i, j);
    }

    private interface Merge<E> {
        E merge(E e1, E e2);
    }

    private class SegmentTree<E> {

        private E[] tree;
        private E[] data;
        private Merge<E> merge;

        public SegmentTree(E[] arr, Merge<E> merge) {
            this.data = data;
            this.merge = merge;
            data = (E[]) new Object[arr.length];
            for (int i = 0; i < arr.length; i++) {
                data[i] = arr[i];
            }
            tree = (E[]) new Object[4 * arr.length];
            buildSegmentTree(0, 0, arr.length - 1);
        }

        private void buildSegmentTree(int treeIndex, int l, int r) {
            if (l == r) {
                tree[treeIndex] = data[l]; // data[r]，此时对应叶子节点的情况
                return;// return 不能忘记
            }
            int mid = l + (r - l) / 2;
            int leftChild = leftChild(treeIndex);
            int rightChild = rightChild(treeIndex);
            buildSegmentTree(leftChild, l, mid);
            buildSegmentTree(rightChild, mid + 1, r);
            tree[treeIndex] = merge.merge(tree[leftChild], tree[rightChild]);
        }

        // 在一棵子树里做区间查询
        public E query(int dataL, int dataR) {
            if (dataL < 0 || dataL >= data.length || dataR < 0 || dataR >= data.length || dataL > dataR) {
                throw new IllegalArgumentException("Index is illegal.");
            }
            return query(0, 0, data.length - 1, dataL, dataR);
        }

        private E query(int treeIndex, int l, int r, int dataL, int dataR) {
            if (l == dataL && r == dataR) {
                return tree[treeIndex];
            }
            int mid = l + (r - l) / 2;
            int leftChildIndex = leftChild(treeIndex);
            int rightChildIndex = rightChild(treeIndex);
            if (dataR <= mid) {
                return query(leftChildIndex, l, mid, dataL, dataR);
            }
            if (dataL >= mid + 1) {
                return query(rightChildIndex, mid + 1, r, dataL, dataR);
            }
            E leftResult = query(leftChildIndex, l, mid, dataL, mid);
            E rightResult = query(rightChildIndex, mid + 1, r, mid + 1, dataR);
            return merge.merge(leftResult, rightResult);
        }


        public int getSize() {
            return data.length;
        }

        public E get(int index) {
            if (index < 0 || index >= data.length) {
                throw new IllegalArgumentException("Index is illegal.");
            }
            return data[index];
        }

        public int leftChild(int index) {
            return 2 * index + 1;
        }

        public int rightChild(int index) {
            return 2 * index + 2;
        }
    }
}

Python 代码：

class NumArray:
    class SegmentTree:

        def __init__(self, arr, merge):
            self.data = arr
            # 开 4 倍大小的空间
            self.tree = [None for _ in range(4 * len(arr))]
            if not hasattr(merge, '__call__'):
                raise Exception('不是函数对象')
            self.merge = merge
            self.__build_segment_tree(0, 0, len(self.data) - 1)

        def get_size(self):
            return len(self.data)

        def get(self, index):
            if index < 0 or index >= len(self.data):
                raise Exception("Index is illegal.")
            return self.data[index]

        def __left_child(self, index):
            return 2 * index + 1

        def __right_child(self, index):
            return 2 * index + 2

        def __build_segment_tree(self, tree_index, data_l, data_r):
            # 区间只有 1 个数的时候，线段树的值，就是数组的值，不必做融合
            if data_l == data_r:
                self.tree[tree_index] = self.data[data_l]
                # 不要忘记 return
                return

            # 然后一分为二去构建
            mid = data_l + (data_r - data_l) // 2
            left_child = self.__left_child(tree_index)
            right_child = self.__right_child(tree_index)

            self.__build_segment_tree(left_child, data_l, mid)
            self.__build_segment_tree(right_child, mid + 1, data_r)

            # 左右都构建好以后，再构建自己，因此是后续遍历
            self.tree[tree_index] = self.merge(self.tree[left_child], self.tree[right_child])

        def __str__(self):
            # 打印线段树
            return str([str(ele) for ele in self.tree])

        def query(self, data_l, data_r):
            if data_l < 0 or data_l >= len(self.data) or data_r < 0 or data_r >= len(self.data) or data_l > data_r:
                raise Exception('Index is illegal.')
            return self.__query(0, 0, len(self.data) - 1, data_l, data_r)

        def __query(self, tree_index, tree_l, tree_r, data_l, data_r):
            # 一般而言，线段树区间肯定会大一些，所以会递归查询下去
            # 如果要查询的线段树区间和数据区间完全吻合，把当前线段树索引的返回回去就可以了
            if tree_l == data_l and tree_r == data_r:
                return self.tree[tree_index]

            mid = tree_l + (tree_r - tree_l) // 2
            # 线段树的左右两个索引
            left_child = self.__left_child(tree_index)
            right_child = self.__right_child(tree_index)

            # 因为构建时是这样
            # self.__build_segment_tree(left_child, data_l, mid)
            # 所以，如果右边区间不大于中间索引，就只须要在左子树查询就可以了
            if data_r <= mid:
                return self.__query(left_child, tree_l, mid, data_l, data_r)
            # 同理，如果左边区间 >= mid + 1，就只用在右边区间找就好了
            # self.__build_segment_tree(right_child, mid + 1, data_r)
            if data_l >= mid + 1:
                return self.__query(right_child, mid + 1, tree_r, data_l, data_r)
            # 横跨两边的时候，先算算左边，再算算右边
            left_res = self.__query(left_child, tree_l, mid, data_l, mid)
            right_res = self.__query(right_child, mid + 1, tree_r, mid + 1, data_r)
            return self.merge(left_res, right_res)

    def __init__(self, nums):
        """
        :type nums: List[int]
        """
        if len(nums) > 0:
            self.st = NumArray.SegmentTree(nums, lambda a, b: a + b)

    def sumRange(self, i, j):
        """
        :type i: int
        :type j: int
        :rtype: int
        """
        if self.st is None:
            return 0
        return self.st.query(i, j)

# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# param_1 = obj.sumRange(i,j)