Frank-wolfe算法多OD对matlab实现
Frank-wolfe算法多OD对matlab实现
- Frank-wolfe算法多OD对matlab实现
-
- Frank-wolfe算法原理
- Frank-wolfe算法流程
- 算例
- 将道路网络抽象为图
- 给定OD对
- 关键函数及完整流程
-
- 1. 搜索每个OD对在网络上的可行径
- 2. Frank-worlfe算法构造
- 3. 主函数
-
- 存在的问题
-
Frank-wolfe算法原理
在无约束最优化问题的基础上,我们可以进一步来求解约束最优化问题。约束最优化问题的一般形式为:
minf(x) m i n f ( x )
s.t.gi(x)≥0,i=1,…,m s . t . g i ( x ) ≥ 0 , i = 1 , … , m
先考虑 gi(x) g i ( x ) 均为线性函数的情况,此时问题与线性规划的约束条件相同,仅仅是目标函数变成了非线性的。我们可以用泰勒展开对目标函数进行近似,将它线性化。将f(x)在xk处展开,有
f(x)≈f(xk)+∇f(xk)T(x−xk) f ( x ) ≈ f ( x k ) + ∇ f ( x k ) T ( x − x k )
故原问题近似于
minf(x)≈f(xk)+∇f(xk)T(x−xk) m i n f ( x ) ≈ f ( x k ) + ∇ f ( x k ) T ( x − x k )
s.t.x∈S s . t . x ∈ S
其中S为线性约束构成的可行域。去掉常量后,问题可以写为
minf(x)≈∇f(xk)Tx m i n f ( x ) ≈ ∇ f ( x k ) T x
s.t.x∈S s . t . x ∈ S
设此问题的最优解为 yk y k ,则直观上 dk=yk−xk d k = y k − x k 应当为原问题的可行下降方向。沿着此方向做一维搜索则可进行一次迭代。为了防止一维搜索的结果超出可行域,我们限制步长0≤λ≤1。注意到线性规划的可行域为凸集,由于 xk x k 和 yk y k 均为可行点,它们确定的连线均在可行域中。限制步长0≤λ≤1保证了一维搜索的结果在可行域中。
更多FW算法原理相关内容,参考
- 线形约束最优化问题的Frank-Worlfe算法
- frankwolfe算法
Frank-wolfe算法流程
算例
将道路网络抽象为图
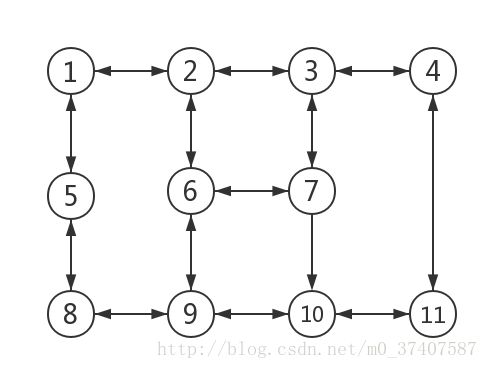
在武汉地区选择一个大型小区,其路网经过梳理后如下图:(其中粗实线表示主干道,而次干道和支路并没有直接分开,可参考道路通行能力上的差异)
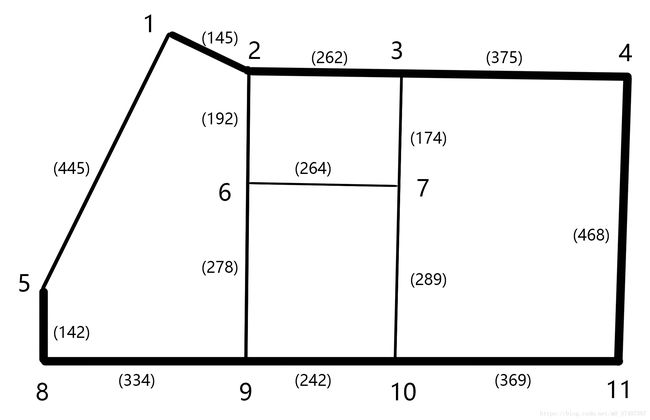
对于该网络,建立邻接矩阵转化为图,给出图上各点间的OD需求,计算图上的交通平衡分布
给定OD对
| 起始点O | 1 | 1 | 1 | 4 | 4 | 4 | 11 | 11 | 11 | 8 | 8 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 目的地D | 4 | 11 | 8 | 1 | 11 | 8 | 1 | 4 | 8 | 1 | 4 |
| 交通量 | 1200 | 1400 | 1600 | 1400 | 1600 | 1200 | 1400 | 1200 | 1400 | 1200 | 1000 |
关键函数及完整流程
1. 搜索每个OD对在网络上的可行径
% 子程序:求解一个OD对间的可行径
function possiablePaths = findPath(Graph, partialPath, destination, partialWeight)
% findPath按深度优先搜索所有可能的从partialPath出发到destination的路径,这些路径中不包含环路
% Graph: 路网图,非无穷或0表示两节点之间直接连通,矩阵值就为路网权值
% partialPath: 出发的路径,如果partialPath就一个数,表示这个就是起始点
% destination: 目标节点
% partialWeight: partialPath的权值,当partialPath为一个数时,partialWeight为0
pathLength = length(partialPath);
lastNode = partialPath(pathLength); %得到最后一个节点
nextNodes = find(0inf); %根据Graph图得到最后一个节点的下一个节点
GLength = length(Graph);
possiablePaths = [];
if lastNode == destination
% 如果lastNode与目标节点相等,则说明partialPath就是从其出发到目标节点的路径,结果只有这一个,直接返回
possiablePaths = partialPath;
possiablePaths(GLength + 1) = partialWeight;
return;
elseif length( find( partialPath == destination ) ) ~= 0
return;
end
%nextNodes中的数一定大于0,所以为了让nextNodes(i)去掉,先将其赋值为0
for i=1:length(nextNodes)
if destination == nextNodes(i)
%输出路径
tmpPath = cat(2, partialPath, destination); %串接成一条完整的路径
tmpPath(GLength + 1) = partialWeight + Graph(lastNode, destination); %延长数组长度至GLength+1, 最后一个元素用于存放该路径的总路阻
possiablePaths( length(possiablePaths) + 1 , : ) = tmpPath;
nextNodes(i) = 0;
elseif length( find( partialPath == nextNodes(i) ) ) ~= 0
nextNodes(i) = 0;
end
end
nextNodes = nextNodes(nextNodes ~= 0); %将nextNodes中为0的值去掉,因为下一个节点可能已经遍历过或者它就是目标节点
for i=1:length(nextNodes)
tmpPath = cat(2, partialPath, nextNodes(i));
tmpPsbPaths = findPath(Graph, tmpPath, destination, partialWeight + Graph(lastNode, nextNodes(i)));
possiablePaths = cat(1, possiablePaths, tmpPsbPaths);
end 2. Frank-worlfe算法构造
function [e,Xn,td] = Frank_wolfe(Q,W,Cmax,Mxf)
%% 1 给定路网数据,OD需求,路段能力
% 计算网络上已知OD集,初始路阻,道路容量,路径路段关系
%==========================================================================
% Q为OD需求,第一行为O,第二行为D,第三行为OD需求
% Cmax为路段能力,是一个节点数乘节点数的矩阵
% mxf为路径路段0-1关系,是一个元胞行向量,元素数量为OD数,每一个成员是一个OD对应的路径路段关系
ODnum = size(Q,2);
W(W == inf) = 1000000;
%==========================================================================
%% 2 自动求出路径和路段数量,根据路段数量定义路段名,给定初始数据
%==========================================================================
numf = zeros(1,ODnum);
for i = 1:ODnum
numf(i) = size(Mxf{1,i},1); % 计算路径数
end
numx = size(Mxf{1,1},2); % 计算路段数
n = sqrt(numx);
syms lambda real
x = sym('x',[1,numx]); % 根据路段数定义路段名
cont=0;
e=inf;
x=x(1:numx); % 路段上的交通量
X0=zeros(1,numx); % 路段上的交通量 数值解
t=zeros(1,numx); % 路段走行函数
%==========================================================================
%% 3 构造阻抗函数并求出初始阻抗,此处用BPR函数
%=======================================================
t=W.*(1+0.15*(x./Cmax).^4); %路段走行时间函数
tt=t;
t=W.*(1+0.15*(X0./Cmax).^4);
t(isnan(t)) = 1000000;
for i = 1:n
t((i-1)*n + i) = 0;
end
Ckrs = cell(1,ODnum);
for i = 1:ODnum
Ckrs{1,i} = (Mxf{1,i} * t');
Ckrs{1,i} = Ckrs{1,i}';
end
%=========================================================
%% 4 全有全无配流
%=========================================================
Min = zeros(ODnum);
index = zeros(ODnum);
for i = 1:ODnum
[Min(i),index(i)]=min(Ckrs{1,i});
end
X1 = zeros(1,numx);
for i = 1:ODnum
tempmatrix = Mxf{1,i};
X1=tempmatrix(index(i),:).*Q(3,i) + X1;
%全有全无法为最短路径上的路段分配流量
end
%=========================================================
%% 5 数据更新
%=========================================================
while e>0.001 %精度判断
cont=cont+1; %迭代次数更新
t=(W).*(1+0.15*(X1./Cmax).^4); %路段时间跟新
td = t;
t(isnan(t)) = 1000000;
for i = 1:n
t((i-1)*n + i) = 0;
end
for i = 1:ODnum
Ckrs{1,i} = (Mxf{1,i} * t'); %路径时间更新
Ckrs{1,i} = Ckrs{1,i}';
end
Min = zeros(ODnum);
index = zeros(ODnum);
for i = 1:ODnum
[Min(i),index(i)]=min(Ckrs{1,i});
end
%全有全无法求辅助流量
Y1 = zeros(1,numx);
for i = 1:ODnum
tempmatrix = Mxf{1,i};
Y1=tempmatrix(index(i),:).*Q(3,i) + Y1; %全有全无法为最短路径上的路段分配流量
end
%Y1=Mxf(index,:).*Q;
S=Y1-X1; %搜索方向
if sum(S) < 0
break;
end
X2=X1+lambda*S; %先将X2用X1和lambda进行表达
t=(W).*(1+0.15*(X2./Cmax).^4); %含lambda的阻抗表达
t(isnan(t)) = 1000000;
f=sum(S.*t,2); %2表示按行求和
lambda1 = 0;
lambda1=double(solve(f)); %求解方程,确定步长。
k=length(lambda1); %如步长lambda1的解不唯一,取实数,且大于0小于1;
for m=1:k
if lambda1(m,1)>=0&&lam
bda1(m,1)<=1
lambda2=lambda1(m,1);
end
end
X2=X1+lambda2*S; %得到下一步的流量值,且进行下一次迭代
e=sqrt(sum((X2-X1).^2))/sum(X1); %精度计算
X1=X2; %流量更新
disp(['迭代次数',num2str(cont),'精度',num2str(e)]);
end
%==========================================================================
Xn = X1;3. 主函数
clc;clear;
%% 构建通行时间费用阻抗矩阵
% 网络中的距离设置,inf表示两点之间无直接相连
n = 11;distance = zeros(n);
distance(1,2) = 145;distance(1,5) = 445;
distance(2,3) = 262;distance(2,6) = 192;
distance(3,4) = 375;distance(3,7) = 174;
distance(4,11) = 468;
distance(5,8) = 142;
distance(6,[7,9]) = [264 278];distance(7,10) = 289;
distance(8,9) = 334;distance(9,10) = 242;distance(10,11) = 369;
distance = distance + distance';
distance(distance == 0) = inf;
distance(1:n+1:n^2) = 0;
distance = distance/1000;% 对角线元素替换成0
% 由道路等级决定的道路设计速度
v0 = zeros(n);
v0(1,2) = 50;v0(1,5) = 40;
v0(2,3) = 50;v0(2,6) = 30;
v0(3,4) = 50;v0(3,7) = 30;
v0(4,11) = 50;
v0(5,8) = 50;
v0(6,[7,9]) = [30 30];v0(7,10) = 30;
v0(8,9) =50;v0(9,10) = 50;v0(10,11) = 50;
v0 = v0 + v0';
v0(v0 == 0) = 0.1;
v0(1:n+1:n^2) = 0; % 对角线元素替换成0
t0 = distance./v0 * 3600;
t0(isnan(t0)) = 0;
%t0 = t0(:);
%% 设置OD矩阵
OD = [1 1 1 4 4 4 11 11 11 8 8 8;
4 11 8 1 11 8 1 4 8 1 4 11;
1200 1400 1600 1400 1600 1200 1400 1200 1400 1200 1000 1300];
% OD矩阵的第一行为O,第二行为D,第三行为该OD对上的OD值
%% 设置道路容量
Cmax = zeros(n);
Cmax(1,2) = 50;Cmax(1,5) = 40;
Cmax(2,3) = 50;Cmax(2,6) = 30;
Cmax(3,4) = 50;Cmax(3,7) = 30;
Cmax(4,11) = 50;
Cmax(5,8) = 50;
Cmax(6,[7,9]) = [30 30];Cmax(7,10) = 30;
Cmax(8,9) =50;Cmax(9,10) = 50;Cmax(10,11) = 50;
Cmax(Cmax == 50) = 1400;
Cmax(Cmax == 40) = 1000;
Cmax(Cmax == 30) = 700;
Cmax = Cmax + Cmax';
Cmax1 = Cmax(:)';
Cmax1(Cmax1 == 0) = 0.01;
% 构造关联矩阵的矩阵向量
odnum = size(OD,2);
mxf = cell(1,odnum);
for i = 1:odnum
O = OD(1,i);D = OD(2,i);
a = findPath(t0,O,D,0);
a = a(:,1:size(a,2)-1);
waynum = size(a,1);
way = zeros(waynum,n*n);
waytemp = zeros(n);
for j = 1:waynum % 对每条可行径
for x = 1:size(a,2)-1
if a(j,x+1) ~= 0
waytemp(a(j,x),a(j,x+1)) = 1;
else
break;
end
end
way(j,:) = waytemp(:);
waytemp = zeros(n);
end
mxf{1,i} = way;
end
% 计算交通在道路网络的分布
tc = t0;
t0 = t0(:)';
[e,Xn,td] = Frank_wolfe(OD,t0,Cmax1,mxf);
X = zeros(n);
for i = 1:n
X(:,i) = Xn(((i-1)*n+1):i*n)';
end
for i = 1:n
tdd(:,i) = td(((i-1)*n+1):i*n)';
end
tdd(tdd == 1000000) = 0;
tz = sum(sum(tdd));
tz0 = sum(sum(tc));
%% 数据导出
% 定义道路等级
zhugandao = [1,2;2,3;3,4;4,11;11,10;10,9;9,8;8,5]';
cigandao = [1,5]';
zhilu = [2,6;6,9;3,7;7,10;6,7]';
for i = 1:size(zhugandao,2)
x= zhugandao(1,i);
y = zhugandao(2,i);
dis_zhu(1,i) = X(x,y); % 正向交通量
dis_zhu(2,i) = X(y,x); % 反向交通量
dis_zhu(3,i) = Cmax(x,y); % 路段容量
dis_zhu(4,i) = dis_zhu(1,i)/dis_zhu(3,i); % 正向v/c比
dis_zhu(5,i) = dis_zhu(2,i)/dis_zhu(3,i); % 反向v/c比
dis_zhu(6,i) = 0;
dis_zhu(7,i) = tdd(x,y); % 路段时间
dis_zhu(8,i) = tdd(y,x); % 反向路段时间
dis_zhu(9,i) = (dis_zhu(7,i)+dis_zhu(8,i))/2; % 平均路段时间
dis_zhu(10,i) = distance(x,y); % 路段长度
dis_zhu(11,i) = dis_zhu(9,i)/3600;
dis_zhu(12,i) = dis_zhu(10,i)/dis_zhu(11,i); % 路段速度
end
zhugandao = [zhugandao;dis_zhu];
zhugandao = sortrows(zhugandao',1);
zhugandao = zhugandao';
for i = 1:size(cigandao,2)
x= cigandao(1,i);
y = cigandao(2,i);
dis_ci(1,i) = X(x,y); % 正向交通量
dis_ci(2,i) = X(y,x); % 反向交通量
dis_ci(3,i) = Cmax(x,y); % 路段容量
dis_ci(4,i) = dis_ci(1,i)/dis_ci(3,i); % 正向负载量
dis_ci(5,i) = dis_ci(2,i)/dis_ci(3,i); % 反向负载量
dis_ci(6,i) = 0;
dis_ci(7,i) = tdd(x,y);
dis_ci(8,i) = tdd(y,x);
dis_ci(9,i) = (dis_ci(7,i)+dis_ci(8,i))/2;
dis_ci(10,i) = distance(x,y);
dis_ci(11,i) = dis_ci(9,i)/3600;
dis_ci(12,i) = dis_ci(10,i)/dis_ci(11,i);
end
cigandao = [cigandao;dis_ci];
for i = 1:size(zhilu,2)
x= zhilu(1,i);
y = zhilu(2,i);
dis_zhi(1,i) = X(x,y); % 正向交通量
dis_zhi(2,i) = X(y,x); % 反向交通量
dis_zhi(3,i) = Cmax(x,y); % 路段容量
dis_zhi(4,i) = dis_zhi(1,i)/dis_zhi(3,i); % 正向负载量
dis_zhi(5,i) = dis_zhi(2,i)/dis_zhi(3,i); % 反向负载量
dis_zhi(6,i) = 0;
dis_zhi(7,i) = tdd(x,y);
dis_zhi(8,i) = tdd(y,x);
dis_zhi(9,i) = (dis_zhi(7,i)+dis_zhi(8,i))/2;
dis_zhi(10,i) = distance(x,y);
dis_zhi(11,i) = dis_zhi(9,i)/3600;
dis_zhi(12,i) = dis_zhi(10,i)/dis_zhi(11,i);
end
zhilu = [zhilu;dis_zhi];
zhilu = sortrows(zhilu',1);
zhilu = zhilu';
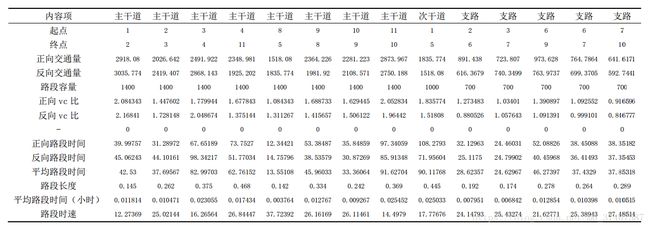
result = [zhugandao,cigandao,zhilu] % 路段信息按列排布,每行的含义参考上文注释存在的问题
当网络中的交通量不大时,在迭代计算中利用sovle函数求解 λ λ 时,会产生不规律复现求解结果为两个复数的情况,目前认为应该是算法的构建中还有数学思想不够完善的地方导致。
进一步完善,敬请期待。
参考博文:配流07—基于BPR函数的Frank Wolfe算法