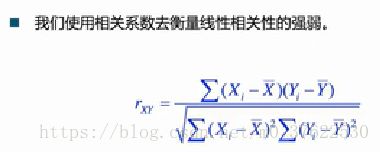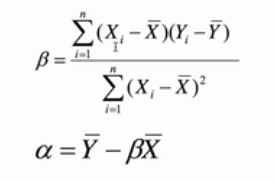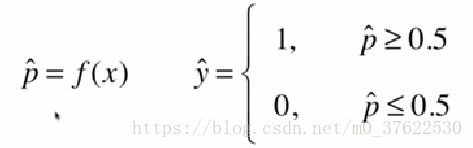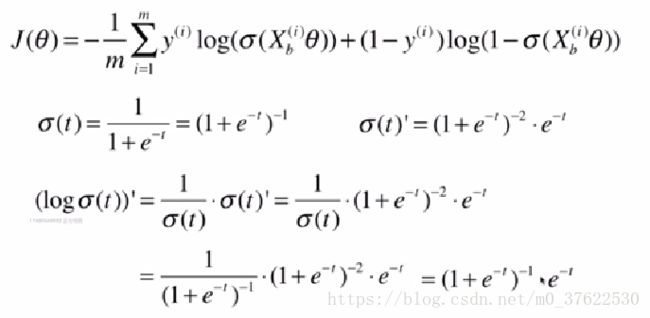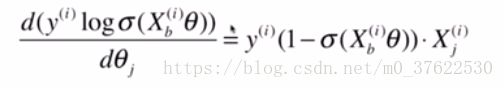线性回归与逻辑回归

本文内容主要基于炼数成金机器学习课程+逻辑回归课程。

也可以配合这篇文章（CS229学习笔记）进行学习。

目录

1 回归问题

2 虚拟变量

3 回归诊断

3.1 发现离群值

3.2 判断线性假设是否合理

3.3 误差是否满足独立、等方差、正态分布？

3.4 多重共线性

4 广义线性回归

5 逻辑回归问题

5.1 Sigmoid函数

5.2 损失函数

5.3 梯度下降

---

1 回归问题

分类：一元线性回归；多元线性（用曲面拟合）；广义线性回归（用线性回归方法处理非线性回归问题）；非线性回归

关系：

相关系数：

相关系数的取值范围为[-1,1]，它的绝对值越接近于1，越适合用直线去拟合。

求各点到直线距离之和 -> 求平行于y轴的线段长度的平方和，称为残差和 -> 令残差和最小

求解上图中的二元一次方程组，解为：

2 虚拟变量

虚拟变量其实算不上一种变量类型（比如连续变量、分类变量等），确切地说，是一种将多分类变量转换为二分变量的一种形式。

比如预测体重w，输入的变量由身高h和性别、人种。其中性别（男or女，暂不考虑复杂情况0）、人种（黄or白or黑，暂不考虑混血等复杂情况）不是连续变量。此时的回归模型为：

w = a + b*h +c*is_man +d*is_yellow + e*is_white

该模型为加法模型。其中is_man，is_yellow，is_white都只能取0或1（能取n个值的变量，在式子中由n-1项表示；比如人种一共三类，则式子中用is_yellow，is_white两个变量表示；否则会造成多重共线性）。

因此我们可以发现，三个哑变量在例子里渠道的作用是调整截距。

如何让哑变量对斜率也产生影响呢？——乘法模型

采用同样的例子，此时回归模型为：

w = a + b*h +c*is_man*h +d*is_woman*h + e*is_yellow*h + f*is_white*h + g*is_black*h

对于乘法模型来说，必须把每个变量所有的情况表示在式子里。

3 回归诊断

3.1 发现离群值

3.2 判断线性假设是否合理

3.3 误差是否满足独立、等方差、正态分布？

首先，让我们承认误差的存在，当预测值加上一个误差时，才能得到实际值： 

第二，我们假设误差服从正态分布。这个假设有两个原因，一个是影响误差的因素有很多，这些因素都是随机分布的，但是它们在整体上会趋向于正态分布，另一个是因为在把误差假设为服从正态分布后，相应的工作一般都能取得比较好的效果，虽然它们还是没有非常精确，但是已经足够了。

3.4 多重共线性

多重共线性是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确。

 

一般来说，由于经济数据的限制使得模型设计不当，导致设计矩阵中解释变量间存在普遍的相关关系。完全共线性的情况并不多见，一般出现的是在一定程度上的共线性，即近似共线性。

 

有的时候,当自变量彼此相关时,回归模型可能非常令人糊涂,估计的效应会随着模型中的其他的自变量而改变数值,甚至是符号,所以我们在分析的时候,了解自变量间的关系的影响是很重要的,因此这个复杂的问题就常被称之为共线性或多重共线性.

 

多重共线性的判别方法是：

 

1）相关系数，如果系数很大，比如0.8以上，高度相关的话，变量间就非常可能存在共线性。

 

2）kappa系数，对相关系数矩阵求k值，如果大于100是较强共线性，大于1000是严重共线性。再通过eigen看存在共线性的变量。

4 广义线性回归

请参考文章：https://blog.csdn.net/m0_37622530/article/details/80953811。

5 逻辑回归问题

解决分类问题——将样本特征和样本发生的概率联系起来，而概率是一个数，所以称为逻辑回归

逻辑回归得到的是一个概率。只能解决二分类问题。

直接使用线性回归的方法，没有值域的限制，而概率是有值域限制的：

所以我们可以把线性回归的解经过一个特殊的函数：

5.1 Sigmoid函数

5.2 损失函数

合并后的损失函数为

其中y=1时的损失函数：

p越小，惩罚越大；p=1时，惩罚为0。

y=0时的损失函数：

该损失函数没有公式解，只能用梯度下降的方法求解；同时由于是凸函数，可以求到全局最优解。

5.3 梯度下降

其中X_j^i是X_b的第i行j列的元素

经过化简后：

（注意前面的系数不一样！）

逻辑回归的向量化：