递归回溯整理(leetcode)
1 求子集 78
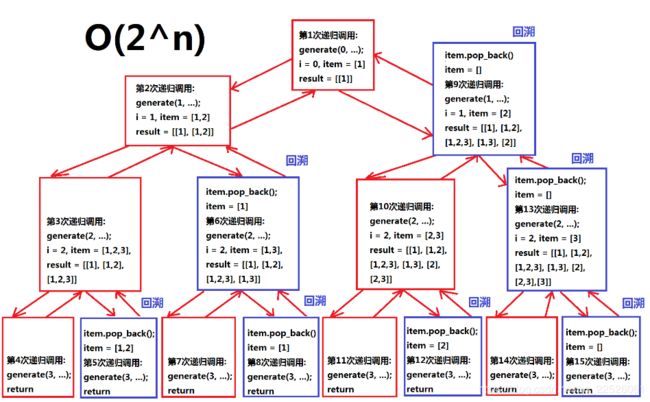
题目:给定nums求所有子集(数组中不含重复元素),以[1,2,3]为例, 8个子集
思路:每个数字都有选和不选两种情况
一步步考虑
先考虑生成[1], [1,2] , [1, 2, 3] 的代码
vector nums = {1, 2, 3};
vector item;
vector> ret;
void generate(vector &item, vector> &ret){
for(int i=0;i 这里注意python 有所不同
nums = [1, 2, 3]
ret = []
item = []
def generate(nums, ret, item):
for i in range(len(nums)):
item.append(nums[i])
ret.append(item.copy()) #之里必须用copy 否则就存成[[1,2,3],[1,2,3],[1,2,3]]
第二步 考虑用递归生成
vector nums = {1, 2, 3};
vector item;
vector> ret;
void generate(int i, vector &item, vector> &ret){
if(i>nums.size(){
return
}
item.push_back(nums[i])
ret.push_back(nums);
generate(i+1, item, ret);
} 然后思考题目
例如 [1,2,3,4,5] 对于第一个元素 我们考虑 两种情况 放入1 和 不放入1, 之后再处理[2, 3, 4, 5]
class Solution {
public:
vector> subsets(vector& nums) {
vector item;
vector> result;
result.push_back(item);
generate(0, nums, result, item);
return result;
}
private:
void generate(int i, vector &nums, vector> &result, vector &item){
if(i >= nums.size()){
return;
}else{
item.push_back(nums[i]);
result.push_back(item);
generate(i+1, nums, result, item);
item.pop_back();
generate(i+1, nums, result, item);
}
}
}; nums = [1, 2, 3] result = [ [ ], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3] ]
2 子集2 90
题目:数组中可能包含重复元素 [2, 1, 2, 2] , 得到[1, 2, 2] 和 [2, 1, 2] 属于一样的
如果光对结果进行去重的话,是无法去重这样的, 可以先对nums进行排序,就不会出现这种情况
class Solution {
public:
vector> subsetsWithDup(vector& nums) {
vector> result;
int num = 1 << nums.size();
sort(nums.begin(), nums.end());
for(int i = 0;i item;
for(int j = 0;j 3 组合数之和2 40
题目: 求这组数所有子集中和为target的的子集
思路:还是应用之前的方法求子集,多存一个cur_sum 如果cur_sum>target 进行剪枝
python版本 看着方便
class Solution:
def combinationSum2(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
ret = []
item = []
cur_sum = 0
candidates.sort()
self.generate(0, candidates, target, cur_sum, ret, item)
return ret
def generate(self, i, candidates, target, cur_sum, ret, item):
if cur_sum > target or i >= len(candidates):
return;
item.append(candidates[i])
cur_sum += candidates[i]
if cur_sum == target and item not in ret:
ret.append(item.copy())
self.generate(i+1, candidates, target, cur_sum, ret, item)
item.pop()
cur_sum -= candidates[i]
self.generate(i+1, candidates, target, cur_sum, ret, item)4 生成括号 22
题目:生成n组括号所有的合法组合
例如 n=3 结果为 ["((()))", "(()())", "(())()", "()(())", "()()()"]
思路:
先考虑生成所有括号,然后对不合法的进行剪枝。 产生子集 对于每个元素时考虑 选与不选两种情况, 对于这道题 对于每个元素是 考虑 是左括号 还是右括号,必定有一个。
生成所有括号代码(python)
def generate(i, n, result, item):
if i>=n:
result.append(item)
return
item += '('
generate(i+1, n, result, item)
item = item[:-1]
item += ')' #回溯的思想
generate(i+1, n ,result, item)
ret = []
item = ''
generate(0, 6, ret, item)
生成了64 个字符串,2**6个
代码可以简化成
def generate(i, n, result, item):
if i>=n:
result.append(item)
return
generate(i+1, n, result, item+'(')
generate(i+1, n ,result, item+')')考虑什么样的放置是不符合的 , 分两方面 1 放左括号:考虑不超过n个, 右括号:不能先与左括号放置,增加两个变量left,right表示还可以放置的左括号数量和右括号数量
class Solution:
def generateParenthesis(self, n):
"""
:type n: int
:rtype: List[str]
"""
result = []
item = ''
self.generate(0, n*2, result, item, n, n)
return result;
def generate(self, i, n, result, item, left, right):
if i>=n:
result.append(item)
return
if left> 0:
self.generate(i+1, n, result, item+'(', left-1, right)
if right > left:
self.generate(i+1, n ,result, item+')', left, right-1)5 N皇后 51
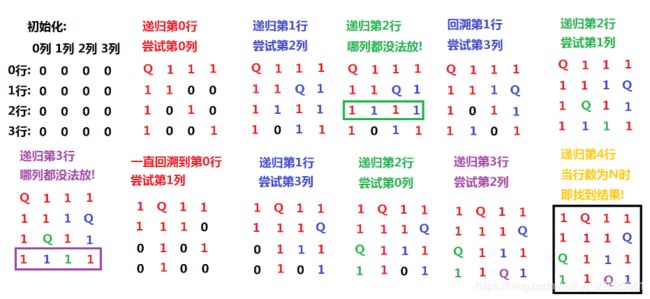
题目:将N个皇后摆放在N*N的棋盘上,有多少种摆放方式
思路:用一个mark数组标记不能摆放的位置,一个一个尝试
先考虑 mark数组的更新代码
def put_down_queen(x, y, mark):
dx = [-1, 1, 0, 0, -1, 1, -1, 1] #构建方向向量
dy = [0, 0, 1, -1, -1, 1, 1, -1]
mark[x][y] = 1
for i in range(1, len(mark)):
for j in range(8):
new_x = x + i*dx[j]
new_y = y + i*dy[j]
if(new_x>= 0 and new_x < len(mark) and new_y>=0 and new_y < len(mark)):
mark[new_x][new_y] = 1最终实现代码
from copy import deepcopy
class Solution:
def solveNQueens(self, n):
"""
:type n: int
:rtype: List[List[str]]
"""
location = [['.' for _ in range(n)] for _ in range(n)]
mark = [[0 for _ in range(n)] for _ in range(n)]
ret = []
self.generate(0, n, mark, ret, location)
c = []
for i in ret:
c.append([''.join(x) for x in i])
return c
def generate(self, k, n, mark, ret, location):
if k == n:
ret.append(deepcopy(location))
else:
for i in range(n):
if mark[k][i] == 0:
temp_mark = deepcopy(mark)
location[k][i] = 'Q'
self.put_down_queen(k, i, mark)
self.generate(k+1, n, mark, ret, location)
mark = temp_mark
location[k][i] = '.'
def put_down_queen(self, x, y, mark):
dx = [-1, 1, 0, 0, -1, 1, -1, 1] #构建方向向量
dy = [0, 0, 1, -1, -1, 1, 1, -1]
mark[x][y] = 1
for i in range(1, len(mark)):
for j in range(8):
new_x = x + i*dx[j]
new_y = y + i*dy[j]
if(new_x>= 0 and new_x < len(mark) and new_y>=0 and new_y < len(mark)):
mark[new_x][new_y] = 1这里注意一个坑, 开始直接用的list.copy 一直不对,后来改成deepcopy 才可以, list.copy值对第一层是深拷贝,对于嵌套的list是浅拷贝,因为嵌套list中存放的是地址