机器学习（二）之线性回归

线性回归(Linear Regression)

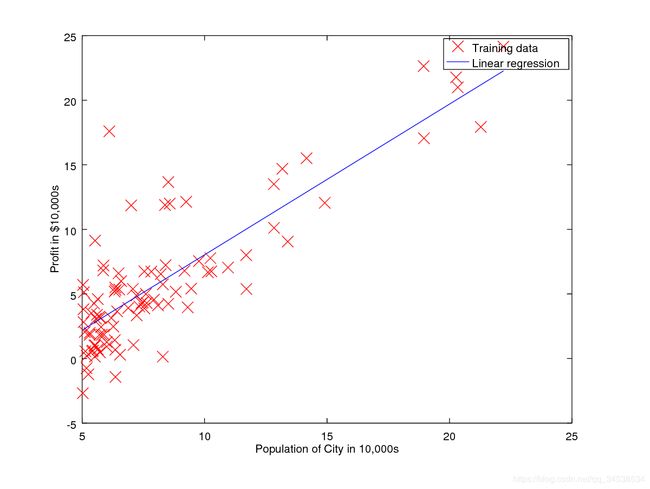
通俗来讲，线性回归就是给定一组数据，将其拟合成为一条直线，使之尽可能精确地刻画该组数据的变化趋势。
比如我们初中学过的直线方程：$y=kx+b$就是一个最简单的线性回归表达式。
直观理解：
给定一组散点如下图，线性回归即是将这组三点拟合成一条直线，使得拟合后的值与给定值误差最小。

单变量线性回归(Linear regression with one variable)

如其名。只存在一个变量的线性回归。最简单的线性回归问题。

1.数学问题表达：

Hypothesis: $h_{\Theta }(x)={\Theta }_0+{\Theta }_{1}x$
Parameters: $ \Theta_0, \Theta_1$
Cost Function: $J({\Theta }_0,{\Theta }_1)=\frac{1}{2m}{\Sigma }_{i=1}^m(h_{\Theta }(x^{(i)})-y^{(i)}{)}^2$
Goal: $minimiz{e}_{{\Theta }_0,{\Theta }_1}J({\Theta }_0,{\Theta }_1)$

如上，线性回归可抽象为最小化目标函数（代价函数）的问题。

2.梯度下降（Gradient Descent）算法：

一种解决函数最小值的算法，用梯度下降算法求代价函数$J({\Theta }_0,{\Theta }_1)$的最小值。

算法表达式：

repeat until converge{
${\Theta }_j:={\Theta }_j-\alpha \frac{\partial }{\partial {\Theta }_j}J({\Theta }_0,{\Theta }_1)(forj=0andj=1)$
#同时更新${\Theta }_0,{\Theta }_1$
}

其中$\alpha$是学习率(Learing rate).它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。
而$\alpha$的选择，对算法十分重要：
太小，收敛太慢；太大，则可能越过局部极小值点，甚至可能无法收敛。
另外，如果初始点已经是局部极小值点了，则不会再改变。

3.梯度下降的线性回归(GradientDescentForLinearRegression)

回顾线性回归与梯度下降问题:

对线性回归问题运用梯度下降法，关键在于求出代价函数的导数，算法可描述为：

称为“批处理”梯度下降。

• 案例：
  给定一组散点，应用梯度下降算法求解线性回归参数$\Theta$，下图蓝线为拟合的线性回归方程。
  
  重要Octave(Matlab)代码：

#计算代价函数
function J = computeCost(X, y, theta)
m = length(y); % number of training examples
J = 0;
J = sum((X * theta - y).^2) / (2*m)
end

#梯度下降算法
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
theta_s=theta;

for iter = 1:num_iters
    theta(1) = theta(1) - alpha / m * sum(X * theta_s - y);
    theta(2) = theta(2) - alpha / m * sum((X * theta_s - y) .* X(:,2));    
    theta_s = theta;   
    % Save the cost J in every iteration    
    J_history(iter) = computeCost(X, y, theta);
end
J_history
end

多元线性回归(Linear Regression with Multiple variables)

1.数学问题表达：

对比单变量线性回归，多变量线性回归多了一些变量（特征）。具体数学表达式为：

Hypothesis: $h_{\Theta }(x)={\Theta }_0+{\Theta }_1{x}_1+{\Theta }_2{x}_2+...+{\Theta }_n{x}_n$
Parameters: ${\Theta }_0,{\Theta }_1,...,{\Theta }_n$
引入$x_0=1$，则公式转化为：$h_{\Theta }(x)={\Theta }^{⊺}x$
Cost Function: $J({\Theta }_0,{\Theta }_1,...,{\Theta }_n)=\frac{1}{2m}{\Sigma }_{i=1}^m(h_{\Theta }(x^{(i)})-y^{(i)}{)}^2$
Goal: $minimiz{e}_{{\Theta }_0,{\Theta }_1}J({\Theta }_0,{\Theta }_1)$

如上，多元线性回归亦可抽象为最小化目标函数（代价函数）的问题。

2.多元梯度下降算法(Gradient Descent for Multiple Variables)

算法表达式：

同样是代价函数对参数求导，不断同时更新参数值，直至收敛。

我们开始随机选择一系列的参数值，计算所有的预测结果后，再给所有的参数一个新的
值，如此循环直到收敛。

梯度下降法之特征缩放

为了梯度下降算法更稳健运行，快速收敛。将不同维度的特征缩放为具有相近的尺度，尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。
原理可见下图：

方法：$x_n=\frac{x_n-{\mu }_n}{S_n}$

其中${\mu }_n$为均值，$S_n$为标准差。

梯度下降法之Debugging and $\alpha$

我们可通过绘制迭代次数和代价函数的图表来观测算法是否收敛以及在何时趋于收敛。如下图：

或者通过将代价函数的变化值与某个阀值（例如 0.001）进行比较，设置为迭代终止条件。
梯度下降算法的每次迭代受到学习率的影响，如果学习率 α 过小，则达到收敛所需的迭
代次数会非常高；如果学习率 α 过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。
通常可以考虑尝试些学习率：
α=0.01， 0.03， 0.1， 0.3， 1， 3， 10

3. 正规方程(Normal Equation)

正则方程也是求解线性回归问题的一种算法，对于某些线性回归问题，正规方程方法是更好的解决方案。

数学问题表达：

求解代价函数最小值，对$J$求偏导，令其=0
利用正则方程求解参数向量：$\Theta =(X^{⊺}X{)}^{-1}{X}^{⊺}y$

在 Octave 中，正规方程写作：pinv(X’*X)*X’*y

梯度下降与正规方程的比较

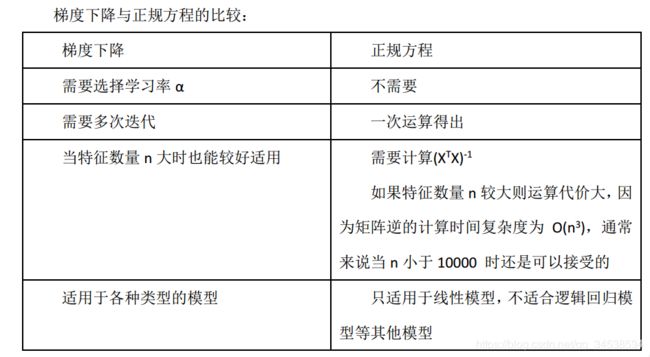
只要特征变量的数目并不大，标准方程是一个很好的计算参数 θ 的替代方法。具体地说，只要特征变量数量小于一万，我们通常使用标准方程法，而不使用梯度下降法。
重要Octave(Matlab)代码：

function [X_norm, mu, sigma] = featureNormalize(X)
X_norm = X;
mu = zeros(1, size(X, 2));      % mean value 均值   size(X,2)  列数
sigma = zeros(1, size(X, 2));   % standard deviation  标准差
  mu = mean(X);       %  mean value 
  sigma = std(X);     %  standard deviation
  X_norm  = (X - repmat(mu,size(X,1),1)) ./  repmat(sigma,size(X,1),1);  
end

function J = computeCostMulti(X, y, theta)
m = length(y); % number of training examples
J = 0;
J = sum((X * theta - y).^2) / (2*m);    
end

function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters)
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
    theta = theta - alpha / m * X' * (X * theta - y); 
    J_history(iter) = computeCostMulti(X, y, theta);
end
end

function [theta] = normalEqn(X, y)
theta = zeros(size(X, 2), 1);
theta = pinv( X' * X ) * X' * y;
end

小结

线性回归算法是解决回归问题的重要算法，对于多项式回归，我们可以通过参数代换，将其转化为线性回归，从而利用梯度下降或正则方程求解。
以上，在此总结。方便查阅、交流。
参考斯坦福大学吴恩达2014机器学习课程.
参考黄海广课程笔记