LADRC的学习——换被控对象进行仿真测试
LADRC控制器的检验——用不同的被控对象测验
一、前文总结
这篇文章主要根据清华大学的硕士陈星写的论文:自抗扰控制器参数整定方法及其热工过程中的应用 进行学习。
参考文献为:
[1] Zhiqiang Gao. Scaling and bandwidth-parameterization based controller tuning[P]. American Control Conference, 2003. Proceedings of the 2003,2003.
[2] 陈星. 自抗扰控制器参数整定方法及其在热工过程中的应用[D].清华大学,2008.
通过上一篇文章搭建了LADC的Simulink仿真模型,通过对这个被控对象,表达式如下:
![]()
可以在简单输入波形的情况下,比如正弦波,方波,三角波等,通过调节omega_c一个参数就能得到较好的控制效果。
如图所示:
方波:
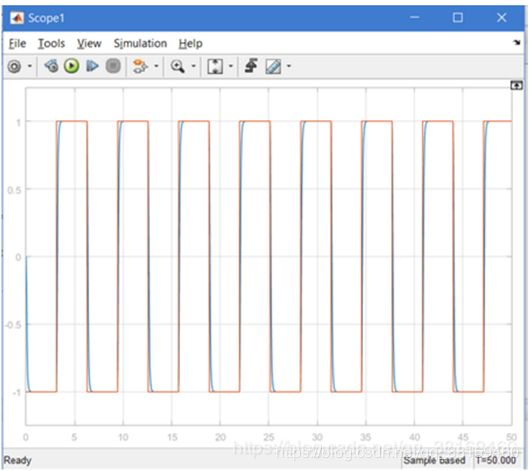
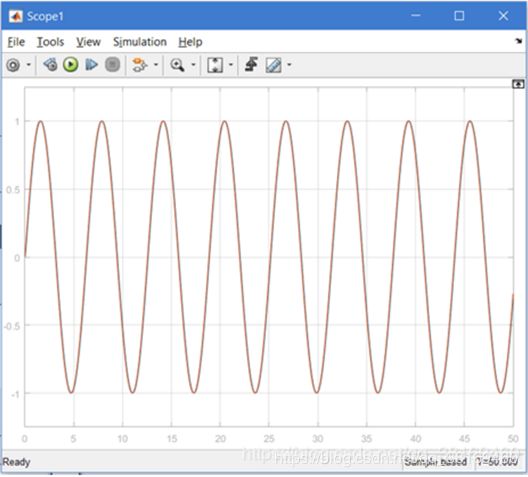
正弦波:
三角波:

通过对结果分析得出结论:
1.模拟仿真对信号的跟踪可以有很好的效果,在快,准,稳这几个方面上都可以极大的满足要求;
2.只用在一定范围内对一个参数omega_c调节,就可以实现对信号的稳定跟踪。
但是在几个地方还没有弄懂:
1.omega_c的调节范围是多少;
2.对哪些信号起到作用;
3.可以应用在哪些被控对象上;
4.如何在LADRC的基础上再扩张,事项更广的应用;
5.LADRC本质是什么;
6.如何编程实现离散LADRC,把它应用在实际生活中。
等等问题,现在我对ADRC还有很多疑问,接下来继续学习扩展,并且深入理解。
二、换被控对象观察控制器控制效果
这里主要引用陈星的硕士论文对LADRC进行理解并学习。
为了进一步改善PID控制器在强干扰及不确定系统中的控制效果,在非线性PID控制的基础上,提出自抗扰控制(ADRC)的概念。其中核心思想是利用扩张状态观测器(ESO)去实时地估计对象的“内扰”和“外扰”,然后利用控制律对总扰动进行补偿,从而使ADRC具有较强的抗扰动能力,并且能够获得较好的性能的鲁棒性。
一般来说,控制系统大家都希望通过数学建模的方法来得到模型,但是无论模型建立的多么精确,实际系统中总会存在未知的动态扰动。实际模型与标称模型的偏差可以看作系统的内扰。还有一些外部扰动,不饶噪声或者控制量扰动,称为外绕,控制系统的内扰和外绕为系统的总扰动。为了获得好的控制结果,采取办法估计系统扰动然后抑制或者消除扰动带来的影响,这就是ADRC的核心思想。
ADRC的特点及其问题:
1.结构简单,与传统PID有着非常简单的结构。例如线性形式的3阶ADRC(指ADRC中的ESO阶数为3),可以看作一个比例微分(PD)控制器加上扩张状态(z3)的观测和补偿,当信号z3被去掉时控制器则完全转为PD控制器。
2.不依赖模型,具有很强的适应性;
3.有很强的抗干扰能力,将系统的非线性,模型不确定性和外部扰动都视为系统的扩张状态加以观测,然后利用控制率进行补偿。
4.解耦特性。自抗扰PID控制方法由于系统变量间的各种耦合作用统一看作扩张状态加以考虑。
其中存在的问题有:
1.参数整定的问题,NLADRC需要整定的参数较多难以进行理论分析。因此出现的简化的LADRC让需要整定的参数大大减少,但是受到观测器带宽的限制。
2.ADRC控制器的设计一般是基于某一阶数的对象而设计的,目前研究最多的是三阶的系统应用与二阶的对象上。目前研究的对象仅仅限制于三阶以内的系统,而且并未给出明确的参数整定规则。
3阶ADRC的结构框图如图:
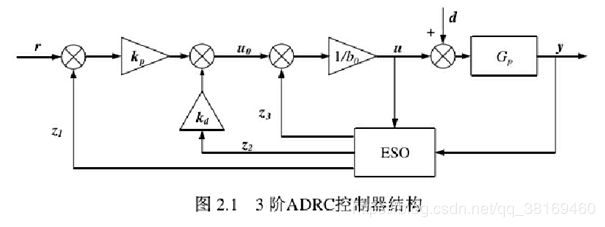
在这里Gp近似作二阶系统,其中 r 为设定值,d为扰动,y为输出,Kp和Kd为PD控制器的系数,u0为控制器参数;ESO为扩张状态观测器,z1,z2,z3分别跟踪y,y‘,f,f 为内部扰动和外部扰动综合。具体推导看引文文献[1],得出结论为:
当ESO可以实现用z3 估计 f 时,可以把控制对象Gp的传递函数看作一个二阶标准型传递函数。
a.LADRC需要调节的几个参数
在实际经验中表明,在二阶以上的控制系统中,b0是影响系统稳定的一个重要参数,因此b0作为一个可调参数将获得更好的控制效果。通过引用文献[1] 的阅读,可以知道需要调节的参数有三个,b0,omega_c,omega_0,其中b0值下的参数稳定域为(omega_0 - omega_c),且b0在一定范围内增大,稳定域也随之增大。
a. b0参数的整定
在这个参数整定过程中,参数b0起到控制系统稳定的作用。系统的稳定域需要足够大以使得满足控制需要的的控制参数处于稳定域之内,然而b0又不能取得太大,否则会使控制信号u过小从而导致系统响应变慢。因此,b0的选择是一个稳定性(鲁棒性)与响应速度的权衡过程。
b.omega_c 和 omega_0 参数整定
(1)Kp和Ki参数化简
由二阶系统可知,Kp和Ki决定ADRC系统的预期动态方程,令:

其中,omega_c为控制带宽,超调量delta%不受它的影响,恒为0,它会影响调节时间ts,并且通过引用文献[1],如果在已知调节时间的条件下,增加一些裕量后计算得出,
(2)观测器参数beta1,beta2,beta3参数整定
这三个参数决定了观测器的精度,通过文献知道,他们可以用观察器带宽omega_0来进行整定,这样观测带宽受到测量噪声或采样频率的限制时将难以取得良好的观测效果。当3阶ESO应用到高阶对象时,omega_0不能取值过大,否则容易造成系统不稳定。在引用文献[1] 中对在omega_0在较小的情况下仍能够获得较好的观测速度,改进了参数整定方法,结论为:
定义跟踪器滞后时间为 Ti 约等于 4/K;然后再 Ti 根据要求取值,从而得到 K , 然后 omega_0 = M*omega_c,M取值在10以内,这里M先取为4再接着进行调节,从而得出三个参数值:
![]()
这样就可实现了参数的整定。
b. 换被控对象进行simulink进行实验
被控对象按照参考文献[1] 的进行测试:
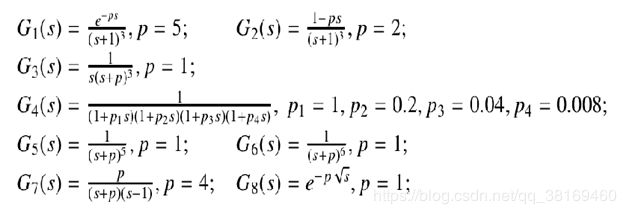
(1对象1:
![]()
对传递函数分析,可以看出这是一个三阶系统,有一个延迟环节,延迟系数为5,因此假设在零初始条件下反拉式变换变为微分方程为:
y’’’ = -3y’’ - 3y’ - y + u(t - 5)1(t - 5)*
把它化为LADRC被控对象的形式:
y’’’ = f + b0u(t - 5)1(t - 5)
其中,f = -3y’’ - 3y’ - y + (1 - b0)u(t - 5)1(t - 5)
因此,我们应该在原来的LADRC的基础上添加 y‘’‘ 作为输入,y , y’ , y‘’作为输出,构建的simulink仿真图像如下:
a.三阶LESO内部图像及其封装图像
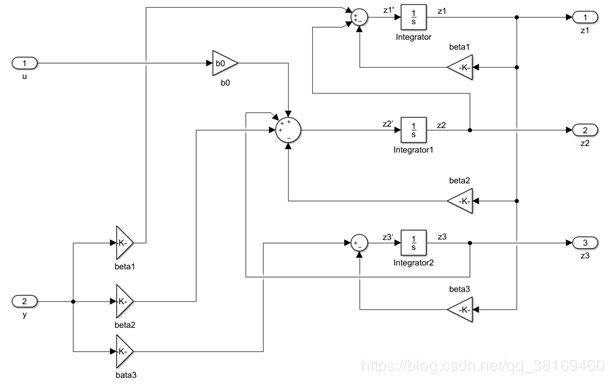
封装图像为:
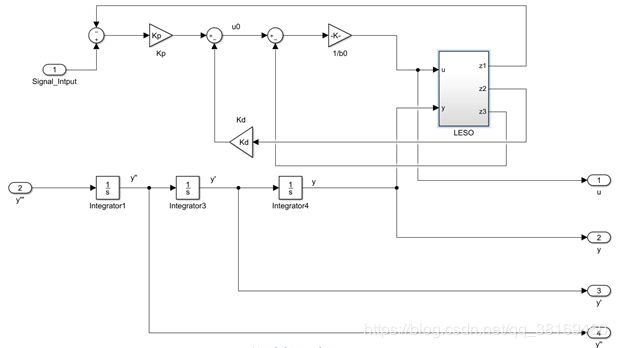
b.LADRC内部仿真图像及其封装图像
封装图像为:
在这里,在上一节的基础上添加了 y’’’ 作为输入, y’’ 作为输出,并把他封装起来,作为控制器LADRC,被控对象如上面化简得到的带延迟环节的三阶微分方程.以后的例子中, a , b 两个部分将不再展示,结构基本不会变化太多,主要展现的第三部分,那里涉及的是被控对象的连接.
c.整体的仿真图像
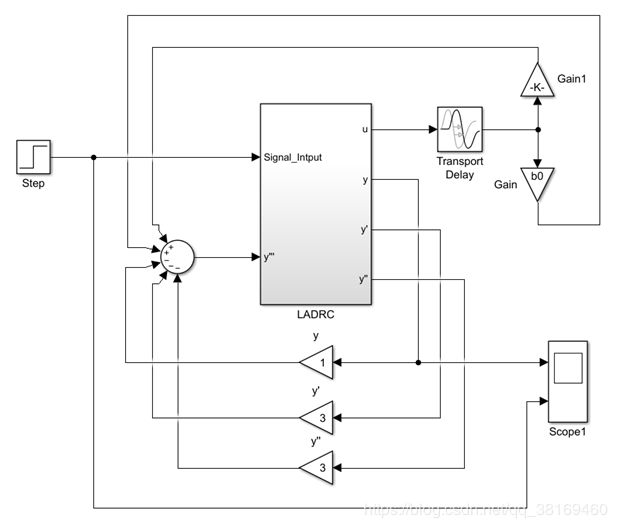
在这里,因为延迟系数为5,转换到时域上为对传函的输入延时为5s,因此这里选择的设定输入只有选择一些低频的信号,对参数 b0, omega_0, omega_c 进行参数整定,看对控制对象的控制情况.
建立一个parameter的m文件,里面对参数进行赋值和调试,看满足条件的参数,其中这个m文件为:
% This is parameter in simulink 'LADRC_Object1'
clear
clc
% Setting Parameter in LARC
b0 = 1.88;
omega_c = 1.015;
omega_0 = 4.06;
xi = 1;
Kp = omega_c.^2;
Kd = 2*xi*omega_c;
beta1 = 3*omega_0;
beta2 = 3*omega_0.^2;
beta3 = omega_0.^3;
sim('LADRC_Object1');
通过这样就可以对模型的参数进行复制,在自己反复测试以后得出,
在这里测试得到 b0 = 1.88 ; omega_c = 1.015 ; omega_0 = 4.06 的时候,系统跟踪阶跃信号的图像为:
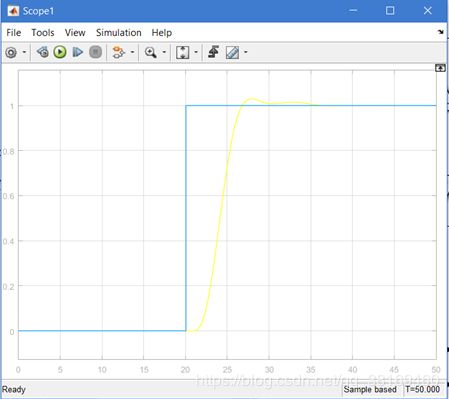
可以看出,通过控制器跟踪系统的输入设定有一定的延迟效应,大约在7s以后可以跟踪到设定值,但是有一定的超调,如果在项目精度范围内,LADRC可以起到较好的控制效果.
(2)对象2
控制对象传递函数为:
![]()
通过对控制对象分析,Gs是非最小相位系统,并且为三阶系统.,通过对被控对象反拉式变换以后得到微分方程为:
y’’’ = -3y’’ - 3y’ - y + u - 2u’
化为标准型为:
y’’’ = f + b0*u
其中 f = -3y’’ - 3y’ - y + (1 - b0)u - 2u’.其整体仿真框图为:
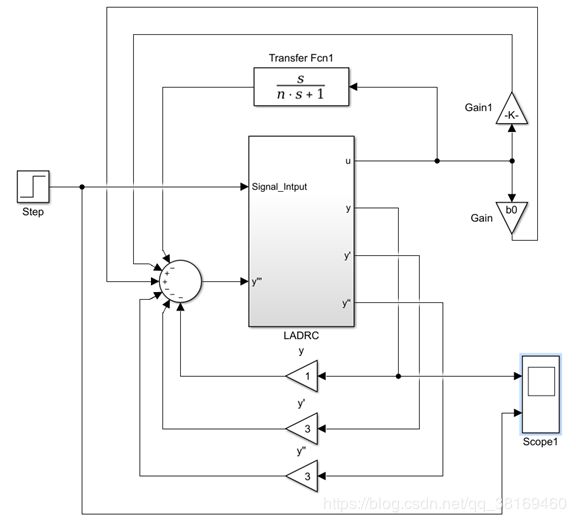
在这个仿真框图中,有一个u的一阶导部分,在simulink中不存在微分模块,因此借鉴Matalb论坛中的方法,建立一个传递函数:G(s) = s/(n*s + 1),当n趋近于0的时候,G(s) 就近似看作微分算子,从而实现微分功能.不过其缺点很明显,仅仅适用于模拟仿真中,实际不能应用,并且n不可能趋近于0,因此只能用很小的数代替,以后考虑解决微分的问题,尽量避开微分.
在这里,参数取为: b0 = 3; omega_c = 1.02; omega_0 = 4.08; n = 0.00001;,得到仿真图像为:
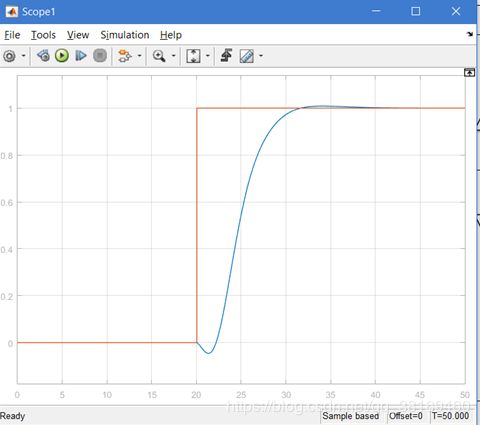
可以看出,输出现了负向的超调,而且延时时间有点长,但是可以很好的满足控制精度,因此LADRC可以应用于非最小相位系统.
(3).对象3
控制对象传递函数为:
![]()
通过对象可知,它是一个四阶系统,可以看作一个三阶系统带有积分环节,可以跟踪斜坡信号,通过拉式反变换得到微分方程为:
y’‘’‘ = -3y’’’ - 3y’’ - y + u
化为标准型为:
y’’’’ = f + b0*u
其中, f = -3y’’’ - 3y’’ - y + (1 - b0)u
其中仿真模型图像为:
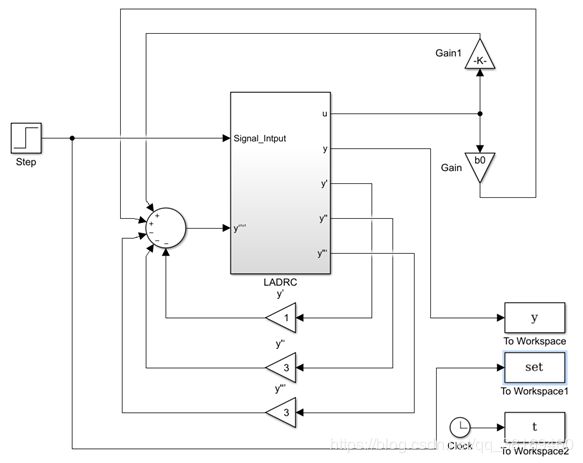
其中,这里加入了三个模块,并且写了在时域上对系统分析的函数。
代码如下:
求解超调量函数:
% Overshoot
function Overshoot = Get_Overshoot(t,y)
Length = length(t);
EndValue = (y(Length) + y(Length - 1) + y(Length - 2))./3;
Ymax = max(y);
if Ymax >= EndValue
Overshoot = 100*(Ymax - EndValue)./EndValue;
else
disp('This system overshoot');
end
求解峰值时间函数:
% Peak Time
function [PeakTime,Ymax,k] = Get_PeakTime(t,y)
[Ymax,k] = max(y);
PeakTime = t(k);
end
求解上升时间函数:
% RiseTime
function RiseTime = Get_RiseTime(t,y)
k = 1; %Forward Subscript
v = 1; %Baxkward Subscript
Length = length(t);
EndValue = (y(Length) + y(Length - 1) + y(Length - 2))./3;
Ymax = max(y);
if Ymax >= EndValue % Overshoot
while y(k) < EndValue
k = k + 1;
end
RiseTime = t(k);
else % No Overshoot
while y(k) < 0.1*EndValue
k = k + 1;
end
v = k;
while y(k) < 0.9*EndValue
v = v + 1;
end
RiseTime = t(v) - t(k);
end
end
这里可以适用于超调和不超调的情况。
获取调节时间
% SettingTime
% Precision can be given 0.02 or 0.05
function SettingTime = Get_SettingTime(t,y,Precison)
Length = length(t);
EndValue = (y(Length) + y(Length - 1) + y(Length - 2))./3;
while (y(Length) > (1 - Precison)*EndValue) && (y(Length) < (1 + Precison)*EndValue)
Length = Length - 1;
end
SettingTime = t(Length);
end
这里Precision参数可以选择的为0.05或者0.02,看要求满足的精度情况。
通过以上函数,我就可以实现在matalb工作空间里面对仿真数据进行操作的分析,其中调节参数代码和分析参数代码如下:
% This is parameter in simulink 'LADRC_Object3'
clear
clc
% Setting Parameter in LARC
M = 12.6;
ts = 34.9;
b0 = 2.7;
omega_c = 10./ts;
omega_0 = M.*omega_c;
k = 4;
xi = 1;
Kp = omega_c.^2;
Kd = 2*xi*omega_c;
beta1 = 3*omega_0;
beta2 = 3*omega_0.^2;
beta3 = k*beta2;
sim('LADRC_Object3');
plot(t,set,t,y);
hold on;
Overshoot = Get_Overshoot(t,y);
PeakTime = Get_PeakTime(t,y);
RiseTime = Get_RiseTime(t,y);
SettingTime = Get_SettingTime(t,y,0.02);
通过调节参数以后得到,其中参数为:
M = 12.6;ts = 34.9;b0 = 2.7;k = 4; 从而得到 b0 = 2.7;omega_c = 0.2865;omega_0 = 3.6103;
通过函数计算得到:超调量为1.6470%,峰值时间为:18.1625,上升时间:16.1573;调节时间:14.5347。对于高阶系统,可以较好的满足的控制需求。其中图像为:
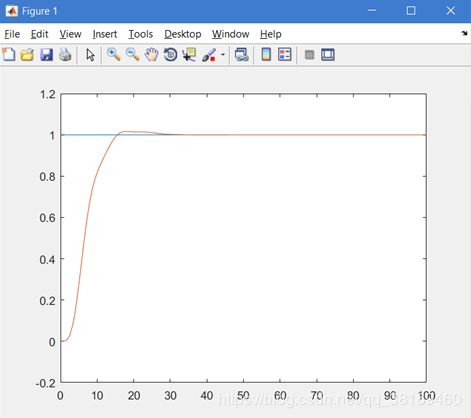
通过调节以后得到的图像可以看出,效果是可以较好的接受的。
(4)对象4
传递函数为:
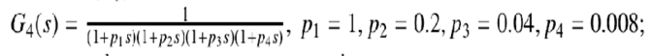
可以看出,这是一个四阶系统,通过Matlab展开,其中代码如下:
>> p1 = 1;
>> p2 = 0.2;
>> p3 = 0.04;
>> p4 = 0.008;
>> syms s;
>> multi = (1 + p1*s)*(1 + p2*s)*(1 + p3*s)*(1 + p4*s);
>> expand_multi = expand(multi);
>> expand_multi
expand_multi =
s^4/15625 + (156*s^3)/15625 + (806*s^2)/3125 + (156*s)/125 + 1
最后得出系统传函,反拉式变换得到微分方程为:
y’’’’ = -156y’’’ - 4030y’’ - 19500y’ - 15625y + 15625u
化为标准形式为:
y’’’’ = f + b0u
其中,f = -156y’’’ - 4030y’’ - 19500y’ - 15625y + (15625 - b0)u
其仿真结构框图和上一个基本一样,只是添加了一个 y 的信号,其中得到仿真图像为:
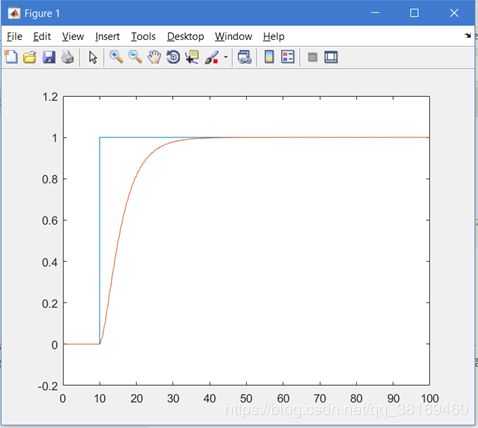
调节参数以后得到上面的图像,其中参数为:
M = 8.6;ts = 23.3;b0 = 1;k = 4; 从而得到 b0 = 1;omega_c = 0.4292;omega_0 = 3.6910;
通过函数计算得到:无超调,上升时间:1.5205;调节时间:20.68。对于这个高阶系统,可以较好的满足的控制需求。
(5)对象5:
传递函数为:
![]()
可以看出,这是一个五阶系统,反拉式变换得到微分方程为:
y’’’’’ = -5y’’’’ - 10y’’’ - 10y’’ - 5y’ - y + u
化为标准形式为:
y’’’’ = f + b0u
其中,f = -5y’’’’ - 10y’’’ - 10y’’ - 5y’ - y + (1 - b0)u
仿真图像为:
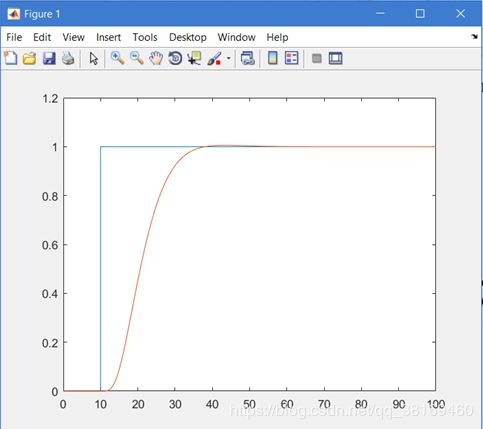
调节参数以后得到上面的图像,其中参数为:
得到 b0 = 414;omega_c = 3.5;omega_0 = 14.2;
通过函数计算得到:超调量为0.5563%,上升时间:13.9302;调节时间:24.1050,峰值时间:33.2334。对于这个五阶系统,可以较好的满足的控制需求。
(6)对象6
传递函数为:
![]()
可以看出,这是一个六阶系统,反拉式变换得到微分方程为:
y_(6) = -6y_(5) - 15y_(4) - 20y_(3) - 15y’’ - 6y - y + u
其中 y_(n) 为 y 的 n 阶导数,化为标准型为:
y’’’’ = f + b0u
其中,f = -6y_(5) - 15y_(4) - 20y_(3) - 15y’’ - 6y - y + (1 - b0)u
仿真框图相对上一个继续添加一个积分项,所以仿真以后得到的图像为:
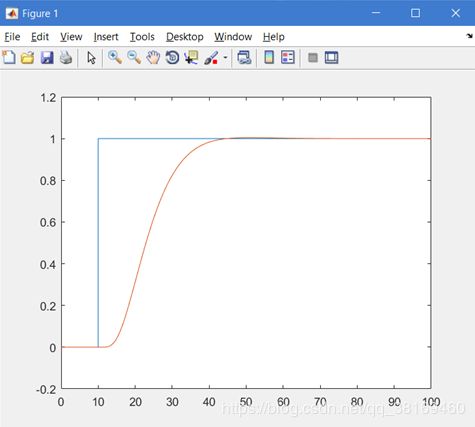
调节参数以后得到上面的图像,其中参数为:
得到 b0 = 500;omega_c = 3.5;omega_0 = 14;
通过函数计算得到:无超调,上升时间:16.5957;调节时间:29.4851,峰值时间:41.0338。对于这个六阶系统,可以较好的满足的控制需求。
(7)对象7
传递函数为:
![]()
可以看出,这是一个非最小相位系统,反拉式变换得到微分方程为:
y’’ = -3y’ + 4y + 4u
化为标准型为:
y’’ = f + b0u
其中, f = -3y’ + 4y + (4 - b0)u
仿真框图中搭建到二阶导数就行,和之前的仿真框图基本不变,所以仿真以后得到的图像为:
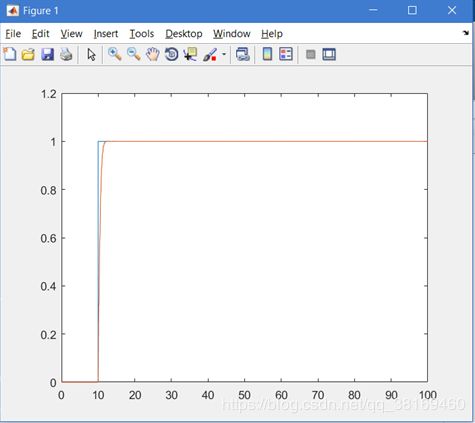
调节参数以后得到上面的图像,其中参数为:
得到 b0 = 1.35;omega_c = 4.59;omega_0 = 15.98;
通过函数计算得到:无超调,上升时间:0.9799;调节时间:1.5523。对于这个非最小相位系统,可以达到很好的控制需求,在响应速度和精度上都35挺好。
(8)对象8
传递函数为:
![]()
可以看出,这是一个类似于延迟环节的传递函数,弄了一整天,泰勒公式展开,搭建类似传函,时域分析,都难以得到解决方案,难以达到理想结果。暂时放弃,以后有机会再试着做一下。
三、实验总结和计划
a.总结
通过对8个控制对象进行模拟仿真和分析,还有调试参数以后得到的结论:
一般来说,系统阶数越高,则b0也会相应的越大;一般调参步骤为,先设定一个合适的omega_c和omega_0,接下来对b0进行调节,调节到b0在某一范围内为发散震荡变为收敛震荡,那么则b0再进行微调,随着b0在一定范围内增大,系统的超调量会减小,但是上升时间会增大。接着调节omega_c,系统的超调量会增大,但是上升时间和调节时间会减小,调节omega_0系统的调节时间会微微减小。
然后b0和omega_c之间有一定的关系,omega_c越大,则b0的将会越大,因此一般先设定omega_c为较小的值,然后调节b0满足要求,接着慢慢增大omega_c进行微调。
然后对于有延迟环节的系统,高阶系统,其调节时间都比较大,但是稳定终值都可以很好的满足项目的精度。对于二阶最小相位和非最小相位系统,通过调节参数,都可以特别好的对信号完成跟踪功能。
b.计划
通过模拟仿真实验,可以发现的理解还在停留在复制的层面,如果想要真正理解LADRC,需要明白几个问题:1.ADRC是PID的改进,那么PID能完成的功能ADRC也应该可以完成,怎么实现串级,和其他控制器配合使用等功能;2.二阶LADRC三阶ESO可以对二阶系统完成特别好的跟踪,对于高阶系统,是否可以对ADRC升阶完成更好的控制效果;3.如何验证LADRC调参效果良好,有什么方法?4.现在仅仅停留在仿真层面,如果要实际应用,我应该怎么写成离散形式,在实际中应用?5.非线性ADRC怎么使用,怎么实现功能?如何对ESO的收敛性证明理解和验证。
接下来学习ADRC的内容可能不会公开,如果有什么需要可以和我讨论,一起进步。

