Count on a tree SPOJ - COT 主席树+lca

题目链接

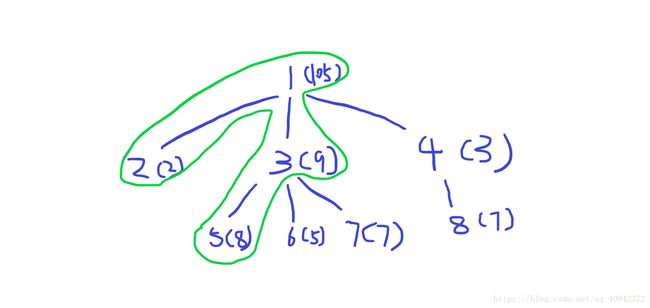
样例解释：

给出n和m表示有n个点和m个询问
下一行有n个值代表对应点的权值
然后是n-1行的u和v，表示u和v相连
最后是m个询问，每个询问有u，v，k，表示u到v这条链上第k大的权值。
如询问 2 5 1 就是图中画出来的这条链中第一个大的权值，那就是2了。

解法：
这道题目跟主席树入门题目：求一段区间第k大很像，不同的是这道题目是求在树的一条链上的第k大。一开始的时候我只感觉到这道题目隐约的跟lca有点关系，但是不知道该如何去处理。然后我看了别人的博客，但是大多数都是直接给出了一个结论：对于查询区间[u,v]，答案就是root[u]+root[v]-root[lca]-root[lca的父亲]上的第k大
一开始不是很理解，后来发现其实类似于前缀和，对于一个节点，它的每个儿子节点做一棵新版本的树。如果从整棵树的根节点开始做的话，最后得到的一个root[u]，就表示了u这个节点到根节点的信息。如果要获得从u到v这条链上的信息，拿就要先算出这两个点的lca，u到lca的信息是通过root[u]-root[lca的父亲]获得的，那么另外的一段就是root[v]-root[lca]获得的。合起来就是那个结论了。
如果不是很理解的话，就举上面图中的例子，节点1是2和5的lca。2到5这条链的信息由2——1和5——3组成。类比一下前缀和，对一个区间[l,r]的询问，答案就是sum[r]-sum[l-1]，所以这里2到1的信息就是root[2]-root[1的父亲]，实际上整棵树有一个虚根0，图中没有画出来，节点1的父亲就是0节点。然后5到3这边就是root[5]-root[3的父亲（也就是1）].然后两端加起来就是整段的信息了，在整段信息中查询第k大就是答案了。
和普通区间求第k大一样，这道题目的权值是离散的，需要离散化一下。

#include
using namespace std;

const int maxn=200005;
const int tp=18;
int n,m;
int tot,cnt,sz;
int root[maxn],lson[maxn*20],rson[maxn*20],tsize[maxn*20];
int head[maxn];
int num[maxn],ls[maxn];
int fa[maxn],dep[maxn];
int f[maxn][tp];

void read(int &m)
{
    char ch;
    int flag = 0;
    while ((ch = getchar()) < '0' || ch > '9')
    {
        if (ch == '-')flag = 1;
    }
    for (m = 0; ch >= '0' && ch <= '9'; ch = getchar())
        m = m * 10 + ch - '0';
    if (flag)
        m *= -1;
}

struct node
{
    int v,nxt;
}edge[maxn*4];

void addedge(int u,int v)
{
    cnt++;
    edge[cnt].v=v;
    edge[cnt].nxt=head[u];
    head[u]=cnt;
}

void updata(int last,int cur,int l,int r,int k)
{


    tsize[cur]=tsize[last]+1;
    lson[cur]=lson[last];
    rson[cur]=rson[last];
    if(l==r)return;
    int mid=(l+r)>>1;
    if(k<=mid)updata(lson[last],lson[cur]=++tot,l,mid,k);
    else updata(rson[last],rson[cur]=++tot,mid+1,r,k);
}

int query(int last,int cur,int lcart,int lcafa,int l,int r,int k)
{
    if(l==r)return l;
    int sum=tsize[lson[last]]+tsize[lson[cur]]-tsize[lson[lcart]]-tsize[lson[lcafa]];
    int mid=(l+r)>>1;
    if(k<=sum)return query(lson[last],lson[cur],lson[lcart],lson[lcafa],l,mid,k);
    else return query(rson[last],rson[cur],rson[lcart],rson[lcafa],mid+1,r,k-sum);
}

int get_ls(int x)
{
    return lower_bound(ls+1,ls+sz+1,x)-ls;
}

void dfs(int now,int fat)
{
    fa[now]=fat;
    dep[now]=dep[fat]+1;
    f[now][0]=fat;
    for(int i=1;i<tp;i++)f[now][i]=f[f[now][i-1]][i-1];
    updata(root[fat],root[now]=++tot,1,sz,get_ls(num[now]));
    for(int i=head[now];~i;i=edge[i].nxt)
    {
        int v=edge[i].v;
        if(v==fat)continue;
        dfs(v,now);
    }
}

int lca(int a,int b)
{
    if(dep[a]>dep[b])swap(a,b);
    if(dep[a]<dep[b])
    {
        int del=dep[b]-dep[a];
        for(int i=0;i<tp;i++)
            if(del&(1<<i))b=f[b][i];
    }
    if(a==b)return a;
    for(int i=tp-1;i>=0;i--)
    {
        if(f[a][i]!=f[b][i])
        {
            a=f[a][i],b=f[b][i];
        }
    }
    return f[a][0];
}

int main()
{
//    freopen("data.in","r",stdin);
    read(n),read(m);
    memset(head,-1,sizeof(head));
    tot=cnt=0;
    for(int i=1;i<=n;i++)
        read(num[i]),ls[i]=num[i];
    sort(ls+1,ls+1+n);
    sz=unique(ls+1,ls+1+n)-ls-1;
    int x,y,z;
    for(int i=1;i<n;i++)
    {
        read(x),read(y);
        addedge(x,y);
        addedge(y,x);
    }
    dfs(1,0);
    for(int i=1;i<=m;i++)
    {
        read(x),read(y),read(z);
        int comfa=lca(x,y);
        printf("%d\n",ls[query(root[x],root[y],root[comfa],root[fa[comfa]],1,sz,z)]);
    }
}