回溯算法进阶——从LeetCode题海中总结常见套路
之前写的一篇:回溯算法——从LeetCode题海中总结常见套路https://xduwq.blog.csdn.net/article/details/105666096
个人来说还是挺有感悟和思考的,写一下第二篇进阶
目录
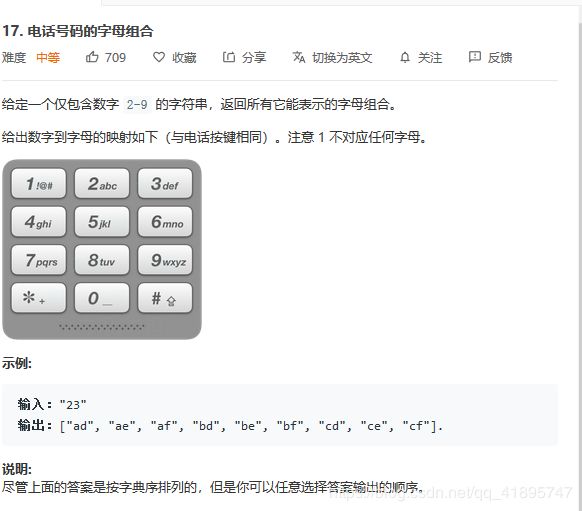
借鉴回溯思想的递归:LeetCode17.电话号码的字母组合
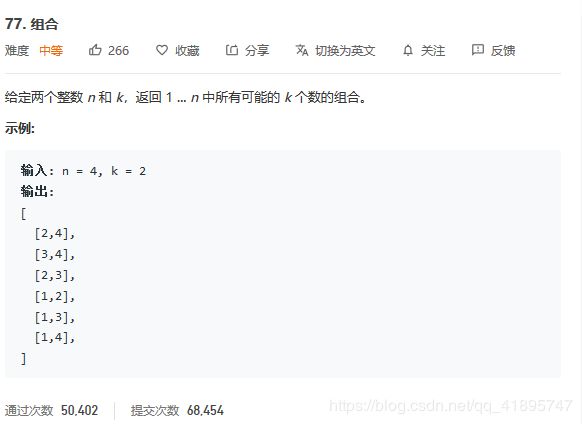
经典可重复回溯框架:LeetCode77.组合
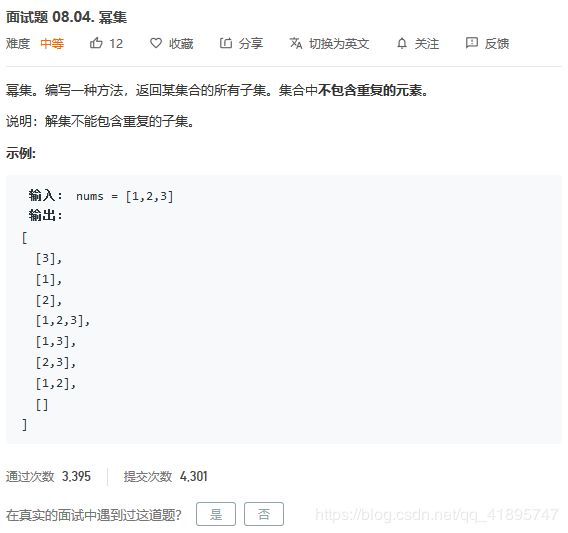
基本不可重复回溯模板题:LeetCode面试题08.04.幂集
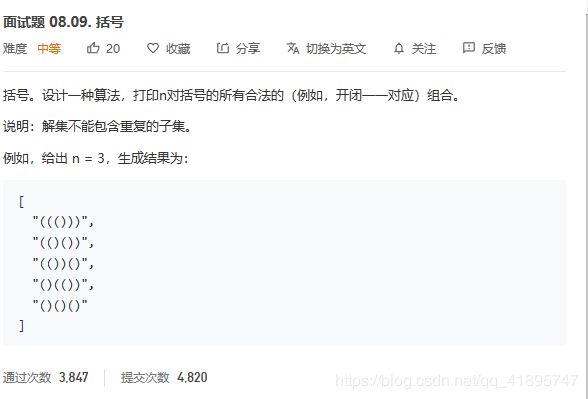
非典型可重复回溯:LeetCode面试题08.09.括号
一步一步优化剪枝的可重复回溯:LeetCode39.组合总和
套用模板不进行剪枝,超时:
可重复计算用的太多,先优化accumulate部分:
将求和步骤写进递归中,彻底优化accumlate
设置回溯函数起始下标进行剪枝
善用this指针和全局变量优化空间复杂度
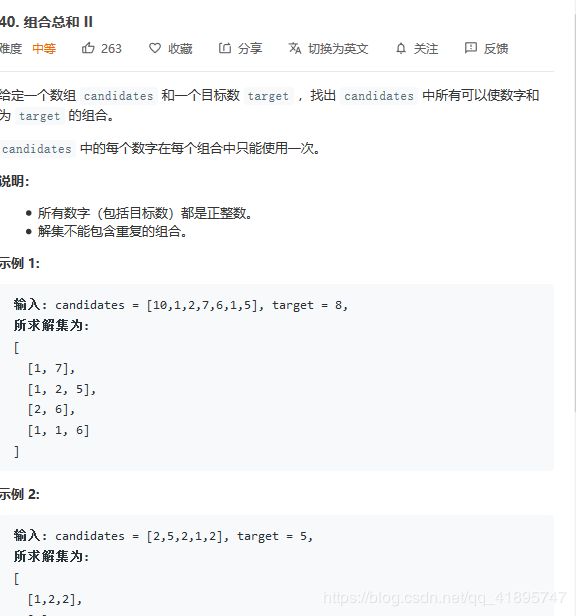
在剪枝上稍作修改的LeetCode40.组合总和II
参考
借鉴回溯思想的递归:LeetCode17.电话号码的字母组合
这一题不是常规的递归,也不是很常规的回溯,很有意思!
考虑一下:
如果给定的digitis大小是2,则两重循环可以搞定:
result = List()
for(i=0;i如果给定的digits大小是3,那么三重循环可以搞定:
result = List()
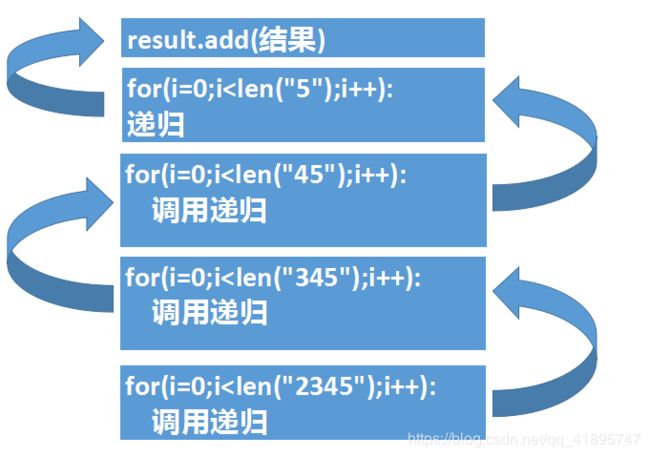
for(i=0;i同理如果digitis的大小是4,那么四重循环可以搞定……
所以咱们这个循环的次数是随着digitis的size来确定的,所以说常规的写for循环的方法肯定无法搞定!
这里就是递归的灵魂来了!
当然,每次递归的所得到的并不是最终可以用的答案,所以在递归开始的时候用if来筛选出符合我们标准的答案
这不也是回溯的小灵魂之一吗?
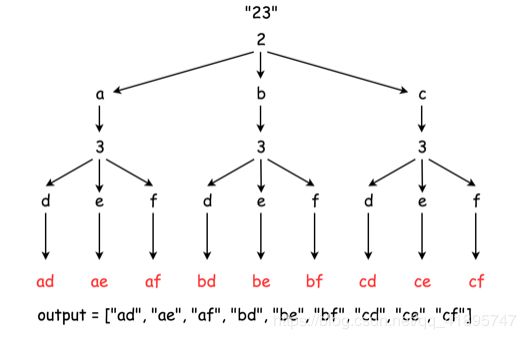
当然,这里的状态树如下,没有回退的步骤,所以说并不存在真正意义上的“回溯”!
class Solution {
public:
vector ans;
vector sList={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};// 字符表
vector letterCombinations(string digits) {
if(digits.size()==0)
return {};
helper(digits, {}, 0);
return ans;
}
void helper(string digits, string s, int index){
if(index==digits.size()){
// 要筛选出符合长度条件的ans
ans.push_back(s);
return;
}else{
int pos = digits[index] - '0'; // 获取对应的下标
string temp = sList[pos]; // 获取对应映射的字符串
for(int i=0;i 经典可重复回溯框架:LeetCode77.组合
最经典的可重复回溯框架,但是如果不剪枝的话,复杂度会比较不理想
剪枝会有一些问题,我暂时还没有完全弄懂
在这里剪枝是这道题的灵魂!
class Solution {
private:
vector> ans;
public:
vector> combine(int n, int k) {
vector temp;
traverback(temp, 1, n, k);
return ans;
}
void traverback(vector temp, int index, int n, int k){
if(temp.size()==k){
ans.push_back(temp);
return;
}
for(int i=index; i<=n-(k-temp.size())+1; i++){ // 剪枝;不剪枝的写法是i<=n
temp.push_back(i);
traverback(temp,i+1, n, k);
temp.pop_back();
}
}
}; 基本不可重复回溯模板题:LeetCode面试题08.04.幂集
class Solution {
private:
vector> ans;
public:
vector> subsets(vector& nums) {
vector temp;
ans.push_back(temp);
traverback(nums,0,temp);
return ans;
}
void traverback(vector& nums, int index, vector temp){
for(int i=index;i 非典型可重复回溯:LeetCode面试题08.09.括号
这道题的思路还是非常有意思的!
如果把n理解为可使用的左括号和右括号的数量,以这个为出发点来思考递归的思路
这道题无非就是需要分别把以n为个数的左右括号数分别用光,所以就有了以下思路的代码:
class Solution {
public:
vector generateParenthesis(int n) {
vector res;
backtrack(res,n,0,"");
return res;
}
// left代表左括号数,rightright代表右括号数
void backtrack(vector& res, int left, int right, string temp){
if(!right&&!left)
res.push_back(temp);
else{
if(left>0)
/*使用一个左括号,同时可使用右括号数加1,这样可避免生成无效括号*/
backtrack(res, left-1, right+1, temp+'(');
if(right>0)
/*可使用的右括号数大于0,则用来补齐原来的左括号*/
backtrack(res, left, right-1, temp+')');
}
}
};
一步一步优化剪枝的可重复回溯:LeetCode39.组合总和
这道题很明显 是可重复回溯模板典例,但是不剪枝的话肯定会超时!
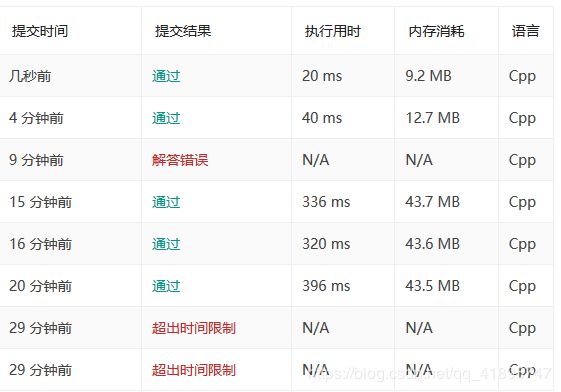
看一下我的优化过程,励志呀!
套用模板不进行剪枝,超时:
class Solution {
public:
vector> ans;
vector> combinationSum(vector& candidates, int target) {
// sort(candidates.begin(),candidates.end());
vector temp;
backtraver(candidates,target,temp);
return ans;
}
void backtraver(vector candidates,int target,vector temp){
if(accumulate(temp.begin(),temp.end(),0)==target){
sort(temp.begin(),temp.end());
if(find(ans.begin(),ans.end(),temp)==ans.end()){
ans.push_back(temp);
return;
}
}
if(accumulate(temp.begin(),temp.end(),0)>target)
return;
for(int i=0;i 可重复计算用的太多,先优化accumulate部分:
还是留下了弱者的泪水……
class Solution {
public:
vector> ans;
vector> combinationSum(vector& candidates, int target) {
sort(candidates.begin(),candidates.end());
vector temp;
backtraver(candidates,target,temp);
return ans;
}
void backtraver(vector candidates,int target,vector temp){
int tempSum = accumulate(temp.begin(),temp.end(),0);
if(tempSum==target){
sort(temp.begin(),temp.end());
if(find(ans.begin(),ans.end(),temp)==ans.end()){
ans.push_back(temp);
return;
}
}
if(tempSum>target)
return;
for(int i=0;itarget){
break;
}else{
temp.push_back(candidates[i]);
backtraver(candidates,target,temp);
temp.pop_back();
}
}
}
}; 将求和步骤写进递归中,彻底优化accumlate
时间上会优化一些,但是没有本质改变!
再次流下弱者的泪水:
class Solution {
public:
vector> ans;
vector> combinationSum(vector& candidates, int target) {
sort(candidates.begin(),candidates.end());
vector temp;
backtraver(candidates,target,temp,0);
return ans;
}
void backtraver(vector candidates,int target,vector temp,int sum){
if(sum==target){
// 还要进行一次去重
sort(temp.begin(),temp.end());
if(find(ans.begin(),ans.end(),temp)==ans.end()){
ans.push_back(temp);
return;
}
}
for(int i=0;itarget){
break;
}else{
temp.push_back(candidates[i]);
backtraver(candidates,target,temp,sum+candidates[i]);
temp.pop_back();
}
}
}
}; 设置回溯函数起始下标进行剪枝
时间复杂度有了一个数量级的提高!
因为每一次调用回溯函数的时候都会少了一个sort和find的步骤!
class Solution {
private:
vector> ans;
public:
vector> combinationSum(vector& candidates, int target) {
sort(candidates.begin(),candidates.end());
vector temp;
backtraver(candidates,target,temp,0,0);
return ans;
}
// 设置起始下标进行剪枝
void backtraver(vector candidates,int target,vector temp,int sum,int start){
if(sum==target){
ans.push_back(temp);
return;
}
for(int i=start;itarget){
break;
}else{
temp.push_back(candidates[i]);
backtraver(candidates,target,temp,sum+candidates[i],i);
temp.pop_back();
}
}
}
}; 善用this指针和全局变量优化空间复杂度
将每次递归调用所需要但不会改变的用全局变量进行处理,空间复杂度大幅优化!
class Solution {
private:
vector> ans;
vector candidates;
int target;
public:
vector> combinationSum(vector& candidates, int target) {
sort(candidates.begin(),candidates.end());
// 递归函数中所要使用的全局变量这样优化可以大幅提高空间复杂度
this->candidates = candidates;
this->target = target;
vector temp;
backtraver(temp,0,0);
return ans;
}
// 设置起始下标进行剪枝
void backtraver(vector temp,int sum,int start){
if(sum==target){
ans.push_back(temp);
return;
}
for(int i=start;itarget)
break;
else{
temp.push_back(candidates[i]);
backtraver(temp,sum+candidates[i],i);
temp.pop_back();
}
}
}
}; 在剪枝上稍作修改的LeetCode40.组合总和II
在上一题的基础上稍作剪枝即可
class Solution {
private:
vector> ans;
vector candidates;
int target;
public:
vector> combinationSum2(vector& candidates, int target) {
sort(candidates.begin(),candidates.end());
// 递归函数中所要使用的全局变量这样优化可以大幅提高空间复杂度
this->candidates = candidates;
this->target = target;
vector temp;
backtraver(temp,0,0);
return ans;
}
// 设置起始下标进行剪枝
void backtraver(vector temp,int sum,int start){
if(sum==target){
if(find(ans.begin(),ans.end(),temp)==ans.end()){
ans.push_back(temp);
return;
}
}
for(int i=start;itarget)
break;
else{
temp.push_back(candidates[i]);
backtraver(temp,sum+candidates[i],i+1);
temp.pop_back();
}
}
}
};
参考
https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number/solution/tong-su-yi-dong-dong-hua-yan-shi-17-dian-hua-hao-m/
https://leetcode-cn.com/problems/combination-sum/solution/hui-su-suan-fa-jian-zhi-python-dai-ma-java-dai-m-2/