Python数据建模--蒙特卡罗模拟

蒙特卡罗模拟

介绍：蒙特卡罗（Monte Carlo）方法，又称随机抽样或统计试验方法，是以概率和统计理论方法为基础的一种计算方法，使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系，用电子计算机实现统计模拟或抽样，以获得问题的近似解。

① π的计算
② 计算积分 y = x**2
③ 排队上厕所问题

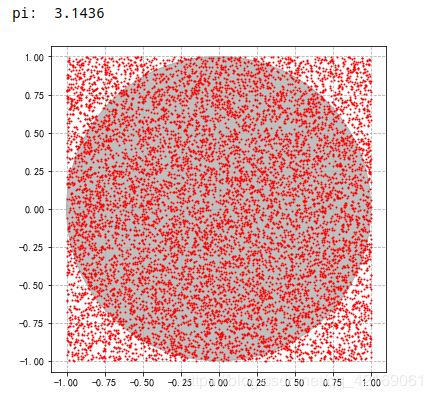
π的计算

引入库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline


from matplotlib.patches import Circle

n = 10000
# 投点次数

r = 1.0           # 半径
a, b = (0., 0.)   # 圆心
# 圆的信息

x_min, x_max = a-r, a+r
y_min, y_max = b-r, b+r
# 正方形区域边界

x = np.random.uniform(x_min, x_max, n) # 均匀分布
y = np.random.uniform(y_min, y_max, n)
# 在正方形区域内随机投点
# numpy.random.uniform(low,high,size) → 从一个均匀分布[low,high)中随机采样，均匀分布

d = np.sqrt((x-a)**2 + (y-b)**2)
res = sum(np.where(d < r, 1, 0))
# 计算点到圆心的距离
# 统计落在圆内的点的数目

pi = 4 * res / n
print('pi: ', pi)
# 计算 pi 的近似值 → Monte Carlo方法：用统计值去近似真实值

fig = plt.figure(figsize = (6,6))
axes = fig.add_subplot(1,1,1)
plt.plot(x,y,'ro',markersize = 1)
plt.axis('equal')
# 制图

circle = Circle(xy = (a,b),radius = r, alpha = 0.5 ,color = 'gray')
axes.add_patch(circle)
plt.grid(True, linestyle = "--",linewidth = "0.8")
plt.show()
# 绘制圆形

*

计算积分 y = x**2

n = 10000
# 投点次数

x_min, x_max = 0.0, 1.0
y_min, y_max = 0.0, 1.0   
# 矩形区域边界

x = np.random.uniform(x_min, x_max, n) # 均匀分布
y = np.random.uniform(y_min, y_max, n)
# 在矩形区域内随机投点

def f(x):
    return x**2
# 创建函数 y = x**2

res = sum(np.where(y < f(x), 1, 0))
# 统计 落在函数 y=x^2图像下方的点的数目

integral = res / n
print('integral: ', integral)
# 计算 定积分的近似值

fig = plt.figure(figsize = (6,6)) 
axes = fig.add_subplot(111) 
axes.plot(x, y,'ro',markersize = 1)
plt.axis('equal') 
# 绘制散点图

xi = np.linspace(0,1,100)
yi = xi ** 2
plt.plot(xi,yi,'--k')
plt.fill_between(xi, yi, 0, color ='gray',alpha=0.5,label='area')  
plt.grid()
# 绘制 y = x**2 面积图

*

厕所排队问题

介绍

# 1、两场电影结束时间相隔较长，互不影响；
# 2、每场电影结束之后会有20个人想上厕所；
# 3、这20个人会在0到10分钟之内全部到达厕所）；
# 4、每个人上厕所时间在1-3分钟之间
# 首先模拟最简单的情况，也就是厕所只有一个位置，不考虑两人共用的情况则每人必须等上一人出恭完毕方可进行。
# 分析：对于每个人都有如下几个参数：
# 到达时间 / 等待时间 / 开始上厕所时间 / 结束时间

实现

arrivingtime = np.random.uniform(0,10,size = 20)
arrivingtime.sort()
workingtime = np.random.uniform(1,3,size = 20)
# np.random.uniform 随机数：均匀分布的样本值

startingtime = [0 for i in range(20)]
finishtime = [0 for i in range(20)]
waitingtime = [0 for i in range(20)]
emptytime = [0 for i in range(20)]
# 开始时间都是0

#print('arrivingtime\n',arrivingtime,'\n')
#print('workingtime\n',workingtime,'\n')
#print('startingtime\n',startingtime,'\n')
#print('finishtime\n',finishtime,'\n')
#print('waitingtime\n',waitingtime,'\n')
#print('emptytime\n',emptytime,'\n')
print('------')

startingtime[0] = arrivingtime[0]  # 第一个人之前没有人，所以开始时间 = 到达时间
finishtime[0] = startingtime[0] + workingtime[0]   # 第一个人完成时间 = 开始时间 + “工作”时间
waitingtime[0] = startingtime[0]-arrivingtime[0]   # 第一个人不用等待

for i in range(1,len(arrivingtime)):
    if finishtime[i-1] > arrivingtime[i]:
        startingtime[i] = finishtime[i-1]
    else:
        startingtime[i] = arrivingtime[i]
        emptytime[i] = arrivingtime[i] - finishtime[i-1]
    finishtime[i] = startingtime[i] + workingtime[i]
    waitingtime[i] = startingtime[i] - arrivingtime[i]
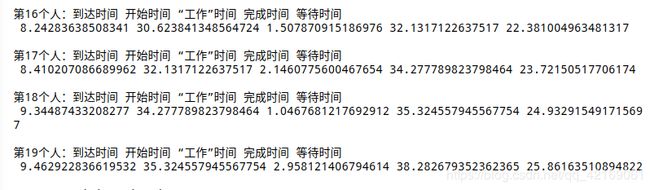
    print('第%d个人：到达时间 开始时间 “工作”时间 完成时间 等待时间\n' %i,
          arrivingtime[i],
          startingtime[i],
          workingtime[i],
          finishtime[i],
          waitingtime[i],
         '\n')
print('arerage waiting time is %f' %np.mean(waitingtime))
print('------')
# 判断：如果下一个人在上一个人完成之前到达，则 开始时间 = 上一个人完成时间，
# 否则 开始时间 = 到达时间，且存在空闲时间 = 到达时间 - 上一个人完成时间

*

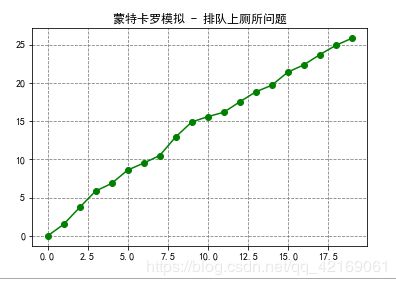
图形展示

fig = plt.figure(figsize = (6,4))
plt.plot(waitingtime, '-go')
plt.grid(True,linestyle='--', color = 'gray',linewidth = '0.8')
plt.title('蒙特卡罗模拟 - 排队上厕所问题')
plt.show()

*

Python 数据建模：

- Python数据建模–回归
- Python数据建模–分类
- Python数据建模–主成分分析
- Python数据建模–K-means聚类
- Python数据建模–蒙特卡洛模拟