概率机器人笔记(3):卡尔曼滤波的理解与简单推导
1.前言
卡尔曼滤波(Kalman Filtering)是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。上面是来自百度百科对卡尔曼滤波的定义,指明了卡尔曼滤波的两大主要功能:过滤噪声和参数估计。
2.卡尔曼滤波的理解和推导
(1)对象模型(Dynamic Model)
对象模型就是卡尔曼滤波适应的问题对象,包括状态转移模型和测量模型,由于引入了高斯噪声,在一定程度上可以模拟现实中的很多问题
{ x t = A x t − 1 + B u t + ω t , ω t ∼ N ( 0 , Q t ) z t = H x t + υ t , υ t ∼ N ( 0 , R t ) \begin{cases} x_t=Ax_{t-1}+Bu_t+\omega_t, & \text {$\omega_t\sim N(0,Q_t)$} \\ z_t=Hx_t+\upsilon_t, & \text{$\upsilon_t\sim N(0,R_t)$} \end{cases} {xt=Axt−1+But+ωt,zt=Hxt+υt,ωt∼N(0,Qt)υt∼N(0,Rt)其中, x t x_t xt是系统的状态, z t z_t zt是测量结果向量, A A A是状态转移矩阵, B B B是控制矩阵, H H H是变换矩阵,作用是状态变换到测量值的维度上,统一单位。 ω t \omega_t ωt和 υ t \upsilon_t υt都服从零均值的高斯分布。
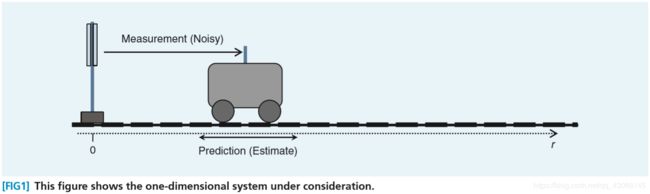
也就是说,在实际模型中,无论是状态(火车速度或者位置)还是传感器的测量(位置传感器)都是存在噪声的,符合我们的认知。
(2)预测模型(Prediction Model)
上述模型由于存在噪声, x t x_t xt不能直接被观测,而模型中的不确定性通过协方差矩阵 P P P来表示。在预测模型中,用 x ^ t − \hat{x}_t^- x^t−表示 t t t时刻由预测模型得到的状态。 P P P是状态中变量的协方差矩阵,根据对象模型,我们可以得到预测模型。
{ x ^ t − = A x ^ t − 1 − + B u t , 预 测 的 均 值 P t − = A P t − 1 − A T + Q t , , 预 测 的 协 方 差 \begin{cases} \hat{x}_t^-=A \hat{x}_{t-1}^-+Bu_t,{预测的均值}\\ P_t^-=AP_{t-1}^-A^T+Q_t,,{预测的协方差}\end{cases} {x^t−=Ax^t−1−+But,预测的均值Pt−=APt−1−AT+Qt,,预测的协方差根据文献1的推导,:
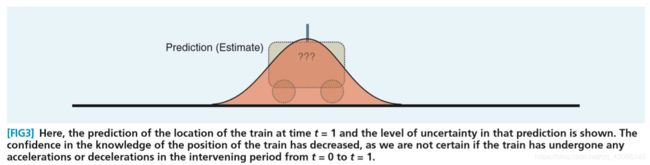
P t − = E [ ( x t − x ^ t − ) ( x t − x ^ t − ) T ] P_t^-=E[(x_t-\hat{x}_t^-)(x_t-\hat{x}_t^-)^T] Pt−=E[(xt−x^t−)(xt−x^t−)T] P t − = E [ ( A ( x t − 1 − x ^ t − 1 − ) + ω t ) ( A ( x t − 1 − x ^ t − 1 − ) + ω t ) T ] P_t^-=E[(A(x_{t-1}-\hat{x}_{t-1}^-)+\omega_t)(A(x_{t-1}-\hat{x}_{t-1}^-)+\omega_t)^T] Pt−=E[(A(xt−1−x^t−1−)+ωt)(A(xt−1−x^t−1−)+ωt)T] = A E [ ( x t − 1 − x ^ t − 1 − ) ( x t − 1 − x ^ t − 1 − ) T ] A T + E ( ω t ω t T ) =AE[(x_{t-1}-\hat{x}_{t-1}^-)(x_{t-1}-\hat{x}_{t-1}^-)^T]A^T+E(\omega_t\omega_t^T) =AE[(xt−1−x^t−1−)(xt−1−x^t−1−)T]AT+E(ωtωtT) = A P t − 1 − A T + Q t =AP_{t-1}^-A^T+Q_t =APt−1−AT+Qt根据对象模型,由于 ω t \omega_t ωt是零均值的高斯分布,当给定状态转移矩阵时,下一时刻分布的均值也就很容易得到了,就是上式的 x ^ t − 1 − \hat{x}_{t-1}^- x^t−1−。比较复杂的是求下一时刻不确定因素的传递,由于我们预测了下一时刻的均值 x ^ t − 1 − \hat{x}_{t-1}^- x^t−1−,预测下一时刻的协方差矩阵自然也是以预测的均值为均值, P t − = E [ ( x t − x ^ t − ) ( x t − x ^ t − ) T ] P_t^-=E[(x_t-\hat{x}_t^-)(x_t-\hat{x}_t^-)^T] Pt−=E[(xt−x^t−)(xt−x^t−)T],由于每一次预测都加上 Q t Q_t Qt,加上运动带来的不确定性m如果不加以修正,预测的不确定性会越来越大,预测函数也会趋于扁平。如下图所示:
(3)测量模型
测量模型由对象模型给出,一般来说,测量数据都是由传感器获得的。
z t = H x t + υ t , υ t ∼ N ( 0 , R t ) z_t=Hx_t+\upsilon_t,\upsilon_t\sim N(0,R_t) zt=Hxt+υt,υt∼N(0,Rt)

(4)更新模型(Update Model)
卡尔曼滤波之所以说是最佳的估计,是因为它结合了预测和测量,而实现这一效果就是把预测和测量的概率密度函数相乘。
下面研究一下两个概率密度函数相乘的情况,具体参考文献2。
y 1 = 1 2 π σ 1 e − ( x − μ 1 ) 2 2 σ 1 2 , y 2 = 1 2 π σ 2 e − ( x − μ 2 ) 2 2 σ 2 2 y_1=\frac{1}{\sqrt{2\pi}\sigma_1}e^{-\frac{(x-\mu_1)^2}{2\sigma_1^2}},y_2=\frac{1}{\sqrt{2\pi}\sigma_2}e^{-\frac{(x-\mu_2)^2}{2\sigma_2^2}} y1=2πσ11e−2σ12(x−μ1)2,y2=2πσ21e−2σ22(x−μ2)2 y 1 y 2 = 1 2 π σ 1 σ 2 e − ( x − μ 1 ) 2 2 σ 1 2 − ( x − μ 2 ) 2 2 σ 2 2 y_1y_2=\frac{1}{2\pi\sigma_1\sigma_2}e^{{-\frac{(x-\mu_1)^2}{2\sigma_1^2}}-\frac{(x-\mu_2)^2}{2\sigma_2^2}} y1y2=2πσ1σ21e−2σ12(x−μ1)2−2σ22(x−μ2)2需要进一步化简成下面的形式 y 1 y 2 = 1 2 π σ f u s e d e − ( x − μ f u s e d ) 2 2 σ f u s e d 2 y_1y_2=\frac{1}{\sqrt{2\pi}\sigma_{fused}}e^{-\frac{(x-\mu_{fused})^2}{2\sigma_{fused}^2}} y1y2=2πσfused1e−2σfused2(x−μfused)2
具体的推导比较复杂,尤其在归一化部分,但是得到下面的结论还是比较简单的
μ f u s e d = μ 1 σ 2 2 + μ 2 σ 1 2 σ 1 2 + σ 2 2 = μ 1 + σ 1 2 ( μ 2 − μ 1 ) σ 1 2 + σ 2 2 = μ 1 + K ( μ 2 − μ 1 ) \mu_{fused}=\frac{\mu_1\sigma_2^2+\mu_2\sigma_1^2}{\sigma_1^2+\sigma_2^2}=\mu_1+\frac{\sigma_1^2(\mu_2-\mu_1)}{\sigma_1^2+\sigma_2^2}=\mu_1+K(\mu_2-\mu_1) μfused=σ12+σ22μ1σ22+μ2σ12=μ1+σ12+σ22σ12(μ2−μ1)=μ1+K(μ2−μ1) σ f u s e d 2 = σ 1 2 σ 2 2 σ 1 2 + σ 2 2 = σ 1 2 − σ 1 4 σ 1 2 + σ 2 2 = σ 1 2 − K σ 1 2 \sigma_{fused}^2=\frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2}=\sigma_1^2-\frac{\sigma_1^4}{\sigma_1^2+\sigma_2^2}=\sigma_1^2-K\sigma_1^2 σfused2=σ12+σ22σ12σ22=σ12−σ12+σ22σ14=σ12−Kσ12 K = σ 1 2 σ 1 2 + σ 2 2 K=\frac{\sigma_1^2}{\sigma_1^2+\sigma_2^2} K=σ12+σ22σ12当预测和测量的单位不一致时,需要将预测的单位转变为测量的单位,然后进行融合: μ f u s e d = μ 1 + K ( μ 2 − H μ 1 ) \mu_{fused}=\mu_1+K(\mu_2-H\mu_1) μfused=μ1+K(μ2−Hμ1) σ f u s e d 2 = σ 1 2 − K H σ 1 2 \sigma_{fused}^2=\sigma_1^2-KH\sigma_1^2 σfused2=σ12−KHσ12 K = H σ 1 2 H 2 σ 1 2 + σ 2 2 K=\frac{H\sigma_1^2}{H^2\sigma_1^2+\sigma_2^2} K=H2σ12+σ22Hσ12令 y 1 y_1 y1为预测模型, y 2 y_2 y2为测量模型
y 1 ∼ N ( x ^ t − , P t − ) , ( μ 1 = x ^ t − , σ 1 2 = P t − ) y_1\sim N(\hat{x}_t^-,P_t^-),(\mu_1=\hat{x}_t^-,\sigma_1^2=P_t^-) y1∼N(x^t−,Pt−),(μ1=x^t−,σ12=Pt−) y 2 ∼ N ( z t , R t ) , ( μ 2 = z t , σ 2 2 = R t ) y_2\sim N(z_t,R_t),(\mu_2=z_t,\sigma_2^2=R_t) y2∼N(zt,Rt),(μ2=zt,σ22=Rt) μ f u s e d = x ^ t , σ f u s e d 2 = P t \mu_{fused}=\hat{x}_t,\sigma_{fused}^2=P_t μfused=x^t,σfused2=Pt带入上式: K = H σ 1 2 H 2 σ 1 2 + σ 2 2 = P t − H T H P t − H T + R K=\frac{H\sigma_1^2}{H^2\sigma_1^2+\sigma_2^2}=\frac{P_t^-H^T}{HP_t^-H^T+R} K=H2σ12+σ22Hσ12=HPt−HT+RPt−HT x ^ t = x ^ t − + K ( z t − H x ^ t − ) \hat{x}_t=\hat{x}_t^-+K(z_t-H\hat{x}_t^-) x^t=x^t−+K(zt−Hx^t−) P t = ( I − K H ) P k − P_t=(I-KH)P_k^- Pt=(I−KH)Pk−
综上所述,卡尔曼算法已经全部推导出来。

完整的卡尔曼滤波公式:
预测模型:
x ^ t − = A x ^ t − 1 − + B u t \hat{x}_t^-=A \hat{x}_{t-1}^-+Bu_t x^t−=Ax^t−1−+But P t − = A P t − 1 − A T + Q t P_t^-=AP_{t-1}^-A^T+Q_t Pt−=APt−1−AT+Qt更新模型: K = P t − H T H P t − H T + R K=\frac{P_t^-H^T}{HP_t^-H^T+R} K=HPt−HT+RPt−HT x ^ t = x ^ t − + K ( z t − H x ^ t − ) \hat{x}_t=\hat{x}_t^-+K(z_t-H\hat{x}_t^-) x^t=x^t−+K(zt−Hx^t−) P t = ( I − K H ) P k − P_t=(I-KH)P_k^- Pt=(I−KH)Pk−
实例:
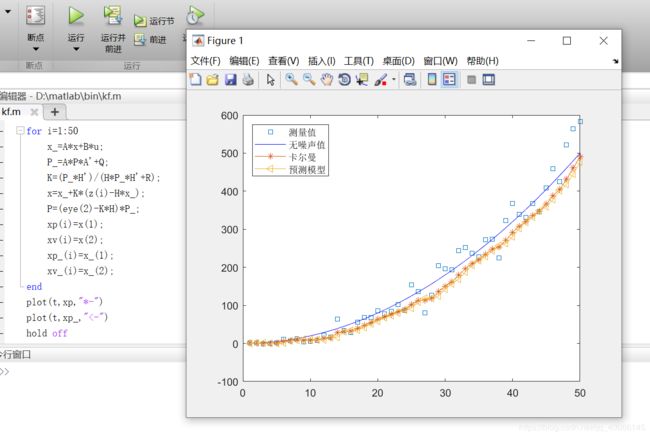
对上面火车的例子进行matlab仿真。
对象模型: [ p t v t ] = [ 1 Δ t 0 1 ] + [ p t − 1 v t − 1 ] + [ Δ t 2 2 Δ t ] + Q t , Q t ∼ N ( 0 , [ 0.0001 0 0 0.0001 ] ) \begin{bmatrix}p_t\\v_t\end{bmatrix}=\begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}+\begin{bmatrix}p_{t-1}\\v_{t-1}\end{bmatrix}+\begin{bmatrix}\frac{\Delta t^2}{2}\\\Delta t\end{bmatrix}+Q_t,Q_t\sim N(0,\begin{bmatrix}0.0001&0\\0&0.0001\end{bmatrix}) [ptvt]=[10Δt1]+[pt−1vt−1]+[2Δt2Δt]+Qt,Qt∼N(0,[0.0001000.0001])
matlab仿真代码:
clc
clear
%*****准备观测值*******%
z=zeros(1,50);
r=zeros(1,50);
figure
for i=1:50
z(i)=0.2*i*i+i*randn();
r(i)=0.2*i*i;
end
t=1:1:50;
plot(t,z,"s")
hold on
plot(t,r,"b-")
x=[0;0];% 初始状态
A=[1 1;0 1];% 状态转移矩阵
P=[1 0;0 1];%状态协方差矩阵
Q=[0.0001,0;0,0.0001];%状态转移的协方差矩阵
H=[1 0];%观测矩阵
R=1;%噪声方差
u=0.01;%加速度1
B=[1/2;1];
xp=zeros(1,50);
xv=zeros(1,50);
xp_=zeros(1,50);
xv_=zeros(1,50);
for i=1:50
x_=A*x+B*u;
P_=A*P*A'+Q;
K=(P_*H')/(H*P_*H'+R);
x=x_+K*(z(i)-H*x_);
P=(eye(2)-K*H)*P_;
xp(i)=x(1);
xv(i)=x(2);
xp_(i)=x_(1);
xv_(i)=x_(2);
end
plot(t,xp,"*-")
plot(t,xp_,"<-")
hold off
3.概率机器人中的卡尔曼滤波
在概率机器人中作为贝叶斯滤波的一个分支,卡尔曼滤波除了需要遵循马尔可夫假设之外,还要遵循以下三个假设:
(1)状态转移概率 P ( x t ∣ u t , x t − 1 ) P(x_t|u_t,x_{t-1}) P(xt∣ut,xt−1)必须是带有随机高斯噪声的连续的线性函数。
x t = A t x t − 1 + B t u t + ε t , ε ∼ N ( 0 , R t ) x_t=A_tx_{t-1}+B_tu_t+\varepsilon_t,\varepsilon\sim N(0,R_t) xt=Atxt−1+Btut+εt,ε∼N(0,Rt)
(2)测量概率 P ( z t ∣ x t ) P(z_t|x_t) P(zt∣xt)也是带有高斯噪声的线性函数
z t = C t x t + δ t , δ ∼ N ( 0 , Q t ) z_t=C_tx_t+\delta_t,\delta\sim N(0,Q_t) zt=Ctxt+δt,δ∼N(0,Qt)
(2)初始状态也服从正态分布
P ( x 0 ) ∼ N ( μ 0 , Σ 0 ) P(x_0)\sim N(\mu_0,\Sigma_0) P(x0)∼N(μ0,Σ0)

从贝叶斯公式角度理解卡尔曼滤波
也可以说从卡尔曼滤波的角度理解贝叶斯滤波,在前上一篇中我们了解了贝叶斯滤波,利用贝叶斯公式推导下面的公式:
P ( x t ∣ z 1 , z 2 , ⋅ ⋅ ⋅ , z t ) = η P ( z t ∣ x t ) P ( x t ∣ z 1 , z 2 , ⋅ ⋅ ⋅ , z t − 1 ) P(x_t|z_1,z_2,···,z_t)=\eta P(z_t|x_t)P(x_t|z_1,z_2,···,z_{t-1}) P(xt∣z1,z2,⋅⋅⋅,zt)=ηP(zt∣xt)P(xt∣z1,z2,⋅⋅⋅,zt−1)其实在这里, P ( z t ∣ x t ) P(z_t|x_t) P(zt∣xt)就是测量模型, P ( x t ∣ z 1 , z 2 , ⋅ ⋅ ⋅ , z t − 1 ) P(x_t|z_1,z_2,···,z_{t-1}) P(xt∣z1,z2,⋅⋅⋅,zt−1)就是预测模型。为了产生递归,同样地将 x t − 1 x_{t-1} xt−1引入预测模型: P ( x t ∣ z 1 , z 2 , ⋅ ⋅ ⋅ , z t ) = η P ( z t ∣ x t ) ∫ x t − 1 P ( x t , x t − 1 ∣ z 1 , z 2 , ⋅ ⋅ ⋅ , z t − 1 ) d x t − 1 P(x_t|z_1,z_2,···,z_t)=\eta P(z_t|x_t)\int_{x_{t-1}}{P(x_t,x_{t-1}|z_1,z_2,···,z_{t-1})}dx_{t-1} P(xt∣z1,z2,⋅⋅⋅,zt)=ηP(zt∣xt)∫xt−1P(xt,xt−1∣z1,z2,⋅⋅⋅,zt−1)dxt−1 = η P ( z t ∣ x t ) ∫ x t − 1 P ( x t ∣ x t − 1 , z 1 , z 2 , ⋅ ⋅ ⋅ , z t − 1 ) P ( x t − 1 ∣ z 1 , z 2 , ⋅ ⋅ ⋅ , z t − 1 ) d x t − 1 =\eta P(z_t|x_t)\int_{x_{t-1}}{P(x_t|x_{t-1},z_1,z_2,···,z_{t-1})}P(x_{t-1}|z_1,z_2,···,z_{t-1})dx_{t-1} =ηP(zt∣xt)∫xt−1P(xt∣xt−1,z1,z2,⋅⋅⋅,zt−1)P(xt−1∣z1,z2,⋅⋅⋅,zt−1)dxt−1 = η P ( z t ∣ x t ) ∫ x t − 1 P ( x t ∣ x t − 1 ) P ( x t − 1 ∣ z 1 , z 2 , ⋅ ⋅ ⋅ , z t − 1 ) d x t − 1 =\eta P(z_t|x_t)\int_{x_{t-1}}{P(x_t|x_{t-1})}P(x_{t-1}|z_1,z_2,···,z_{t-1})dx_{t-1} =ηP(zt∣xt)∫xt−1P(xt∣xt−1)P(xt−1∣z1,z2,⋅⋅⋅,zt−1)dxt−1 本 时 刻 的 最 佳 估 计 = η ∗ 测 量 模 型 ∗ 预 测 模 型 ( 状 态 转 移 ∗ 上 一 时 刻 的 最 佳 估 计 ) 本时刻的最佳估计=\eta*测量模型*预测模型(状态转移*上一时刻的最佳估计) 本时刻的最佳估计=η∗测量模型∗预测模型(状态转移∗上一时刻的最佳估计)
参考文献:
1.Faragher, Ramsey. Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation [Lecture Notes][J]. IEEE Signal Processing Magazine, 2012, 29(5):128-132.
2.P.A. Bromiley. Products and Convolutions of Gaussian Probability Density
Functions