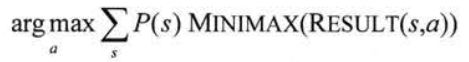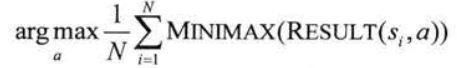第五章 对抗搜索
博弈
定义
博弈, 即对抗搜索问题, 指在竞争环境中, 每个Agent的目标间是冲突的.
零和游戏, 游戏结束时效用值总是相等且符号相反.
提升效率
剪枝: 在搜索树中忽略不影响最后决定的部分.
启发式的评估函数: 在不进行搜索的情况下估计某状态的效用值.
MAX和MIN游戏的形式化
S0: 初始状态
PLAYER(s): 定义此时谁行动
ACTIONS(s): 返回此状态下的合法行动集合
RESULT(s, a): 转移模型, 定义行动的结果
TERMINAL-TEST(s): 终止测试
UTILITY(s, p): 效用函数, 定义p在终止状态s下的数值
博弈中的优化决策
类似于AND-OR算法, MAX需要制定应急策略, 需要考虑MIN的每种可能行动.
假设每个玩家都按最优策略行棋, 那么结点的极小极大值就是对应状态的效用值. MAX偏向于移动到有极大值的状态, MIN偏向于移动到有极小值的状态.
对应的博弈树: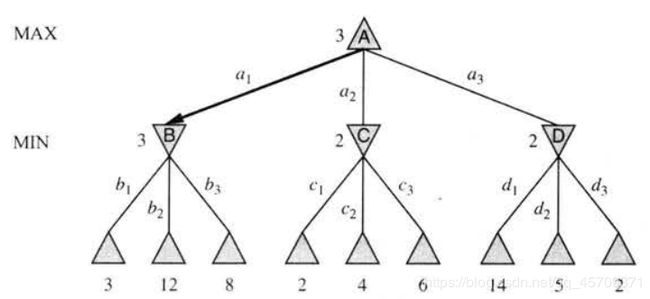
公式:
极小极大算法
递归到叶结点, 然后将值回传.
相当于MAX决定走哪一步之前, 需要不停想下一步MIN怎么走, 下下步我怎么走…直到走到最终状态, 然后再决定我这一步究竟该怎么走.
多人博弈
采用向量表示状态效用值.
α-β剪枝
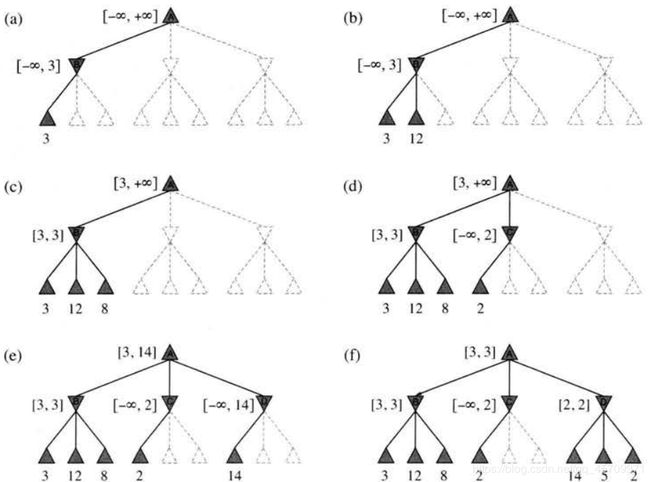
当前结点值未知, 范围为[-∞, +∞], 递归地去探索子结点, 直到遇到终止状态, 然后开始回写(递归地缩小父结点的范围), 并判断是否需要继续探索其它子结点.
另一种表述: 选手移动到结点n, 但如果n的父结点或祖先结点上有更好的选择m, 选手就永远不会到达n, 所以一旦发现n的足够信息(通过检查它的后代), 就可以剪裁它.
名称含义
α = 目前为止路径上发现的MAX的最佳选择
β = 目前为止路径上发现的MIN的最佳选择
搜索中不断更新α和β, 一旦发现某个结点的α或β比现在的值更差时, 就剪裁这个结点剩下的分支.
行棋排序
若能检查结点能够采取最佳优先的顺序(即尽量多地裁剪), 效率为O(bm/2)而非O(bm), 相当于有效分支因子变为b1/2.
理解:
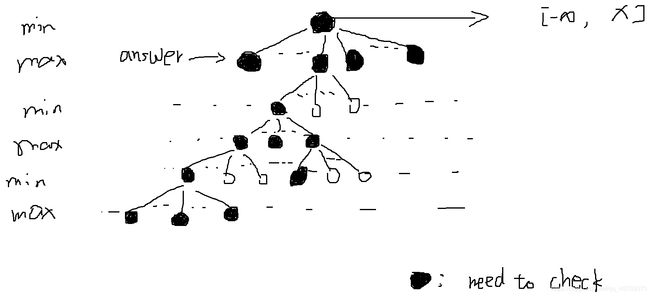对于min层, 只需检查一个结点; 对于max层, 需要检查所有结点.
N(结点数) = 2 * (b0 + b1 + … + bm/2) = O(bm/2)
若检查后继状态为随机顺序, 那么要检查的结点数为O(b3m/4).
提高效率的一些方法: 增加行棋排序方案(比如优先执行哪些步), 维护换位表(记录以前出现过的棋局)
对比极小极大算法和α-β算法: 前者需要生成整个博弈的搜索空间, 后者可以剪裁掉一大部分.
不完美的实时决策
用估计棋局效用值的启发式评估函数EVAL取代效用函数, EVAL的截断测试取代终止测试.
启发式极小极大值:
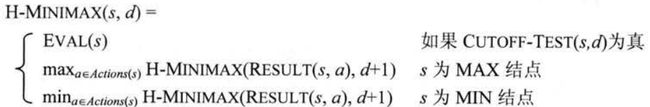
评估函数
对于终止状态, 排序结果不变; 对于非终止状态, 返回一个根据取胜几率的期望值(可以根据当前棋局的特征评估).
截断搜索
最直接的方式是设置固定的深度限制, 当达到该限制或者到了终止结点时CUTOFF-TEST(state, depth)返回true. 更好的方法是采用迭代深入.
地平线效应: 一些实际上无法避免的事情, 通过将它推出当前的搜索深度之外, 来认为自己避免了那件事情.
单步延伸: 在给定棋局中发现一种较好的棋招, 就记住它, 当搜索深度达到限制时, 若此单步延伸合法, 则考虑此棋招.(这样做可能会超过深度限制, 但由于单步延伸很少, 不会增加太多开销)
向前剪枝
在某个结点上无需进一步考虑而直接剪裁一些子结点.
概率截断算法: 根据以前的经验估计深度d上的值v是否可能在(α, β)范围外.
搜索与查表
开局前几步的棋局状态大都常见, 因此可以通过查表; 之后的行棋就通过搜索; 博弈接近尾声时的棋局可能性有限, 因此又恢复到查表.
随机博弈
加入机会结点, 值为所有子结点的期望:
部分可观察的博弈
蒙特卡洛近似:
