《Grokking Deep Learning》 神经学习

神经学习

1、神经网络精准预测与否？

预测就是一个神经网络

knob_weight = 0.5  #初始化权重参数（预测的标准）
input = 0.5 #输入值
goal_pred = 0.8  #真实情况，f(0.5)=0.8
pred = input * knob_weight  #预测值=输入*权重
error = (pred - goal_pred) ** 2   #误差
print(error)#输出误差

输入*权重=预测值（和真是可能有差距）
为什么要用平方呢？
是因为能够让这个值一直保持为正。

训练神经网络的目标是做出正确的预测。这就是你想要的。在最务实的世界里，你希望网络接受你可以轻松计算的输入(今天的股价)，并预测难以计算的东西(明天的股价)。这就是神经网络有用的原因

2、为什么要衡量误差？

衡量误差简化了问题，改变旋钮权重以使网络正确预测目标预测比改变旋钮权重以使误差== 0 要稍微复杂一些。用
这种方式来看待这个问题有一些更简洁的东西。最终，这两种说法说的是同一件事，但试图将错误设为 0 似乎更简单。

通过平方误差，小于 1 的数字变小，而大于 1 的 数字变大。这样更大的错误变得非常大，而更小的错误很快变得无关紧要。
通过这种方式测量误差，可以将大的误差优先于小的误差。当有较大的纯误差时(比如说，10)，会告诉自己有很大的误差(10 * 2 == 100)；相反，当有小的纯误差时(比如说，0.01)，会告诉自己有非常小的误差(0.01 * 2 == 0.0001)。
相反，如果取绝对值而不是平方误差，就不会有这种类型的优先级

3、热和冷学习

首先搭建神经元函数：

weight = 0.1 
lr = 0.01
def neural_network(input, weight):
 prediction = input * weight
 return prediction

预测、初始化一个weight：

number_of_toes = [8.5]
win_or_lose_binary = [1] 
input = number_of_toes[0]
true = win_or_lose_binary[0]
pred = neural_network(input,weight)
error = (pred - true) ** 2
print(error)

接下来用更高的权重和评估误差进行预测：

lr = 0.1  #用于纠正 
p_up = neural_network(input,weight+lr)  # 让预测值学习成更高的做法
e_up = (p_up - true) ** 2
print(e_up)

用更低的权重和评估误差进行预测：

lr = 0.01
p_dn = neural_network(input,weight-lr)
e_dn = (p_dn - true) ** 2
print(e_dn)

比较误差并设置新的重量：

if(error > e_dn || error > e_up):
if(e_dn < e_up): weight -= lr
if(e_up < e_up): weight += lr

这最后五个步骤是冷热学习的一次迭代。这个迭代本身就让我们非常接近正确的答案。
神经网络学习的真正含义:搜索问题。正在搜索权重的最佳配置，以便网络误差降至 0(并完美预测)。和所有其他形式的搜索一样，可能找不到你要找的东西，即使找到了，也可能需要一些时间。

不断地尝试的方式，以及导数的方式，寻找梯度最低。

import time

weight = 0.5
input = 0.5
goal_prediction = 0.8
step_amount = 0.001
for iteration in range(1101):
    time.sleep(0.1)
    prediction = input * weight
    error = (prediction - goal_prediction) ** 2
    print("Error:" + str(error) + " Prediction:" + str(prediction))
     
    up_prediction = input * (weight + step_amount)
    up_error = (goal_prediction - up_prediction) ** 2
    down_prediction = input * (weight - step_amount)
    down_error = (goal_prediction - down_prediction) ** 2
    if(down_error < up_error):
        weight = weight - step_amount
     
    if(down_error > up_error):
        weight = weight + step_amount

运行结果

做出预测后，你再预测两次，一次是用稍高的权重，另一次是用稍低的权重。然后根 据哪个方向给出的误差较小来移动重量。重复这个足够的次数最终会将错误减少到 0。
不一定是某个些指定的次数迭代，主要是看多久能得到最优结果

4、从误差中，同时计算误差的方向和误差的程度

测量一下误差，找出 direction和amount：

weight = 0.5
goal_pred = 0.8
input = 0.5
for iteration in range(20):
 pred = input * weight
 error = (pred - goal_pred) ** 2
 direction_and_amount = (pred - goal_pred) * input
 weight = weight - direction_and_amount
 print("Error:" + str(error) + " Prediction:" + str(pred))

发现只用了20次就非常接近0.8

5、梯度下降

所有的思想源自于前牛顿思想，目前所有的深度学习的梯度下降算法的优化，实质上都是尽可能的去根据【牛顿迭代法】做各种简化或者变换。
梯度下降和这种实现的主要区别是新的变量增量。这是节点过高或过低的原始数量。不是直接计算方向 和数量，而是首先计算输出节点的不同程度。只有这样，才能计算方向和量来改变权重

练习

1# 调试54页的代码，实验不同结果，总结规律

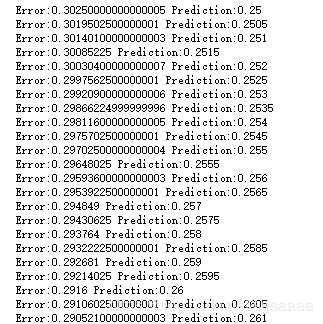
随着程序的运行error越来越小，预测值越来越接近0.8
将step_amout改成1：

一直在跳动没有收敛
step_amout的值设置不对得不到最终的结果
将weight设置为0.1：

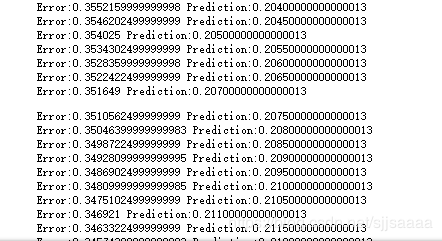
error值也是逐渐在减小，预测值越来越大，只是幅度小。

如果尺度过大就永远得不到最终的结果，对算法做几次预测，进行改进运算，改进后，只需要一次预测即可每次迭代。本质还是一样，但是在数学上进行了优化。

2# 网上查找一下【牛顿迭代法】的资料，并且总结
在方程f(x)=0的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根，此时线性收敛，但是可通过一些方法变成超线性收敛
在可以用迭代算法解决的问题中，至少存在一个可直接或间接地不断由旧值递推出新值的变量，这个变量就是迭代变量。
迭代关系式，指如何从变量的前一个值推出其下一个值的公式（或关系）。迭代关系式的建立是解决迭代问题的关键，通常可以使用递推或倒推的方法来完成
不能让迭代过程无休止地执行下去。迭代过程的控制通常可分为两种情况：一种是所需的迭代次数是个确定的值，可以计算出来；另一种是所需的迭代次数无法确定。对于前一种情况，可以构建一个固定次数的循环来实现对迭代过程的控制；对于后一种情况，需要进一步分析得出可用来结束迭代过程的条件。

3# 运行56页代码，调整参数看结果的变化，对比和上一个算法的差别。

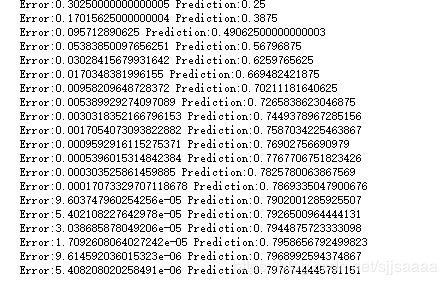
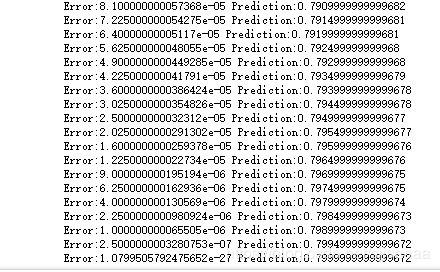
原来很多次的迭代，现在只需要20次迭代就非常接近0.8
大大减少了迭代的次数和时间的消耗，而程序也相对来说比较简单。

4# 构造一个只有一个输入和一个输出的生活中的问题，尝试用神经元去预测和学习解决训练神经元解决。

对于抛硬币正反面能否达到一半的概率