cs231n学习笔记-lecture4（Backpropagation and Neural Networks）以及作业解答

Backpropagation

学习笔记

这部分主要是比较详细的介绍使用计算树进行反向传播的计算方法。

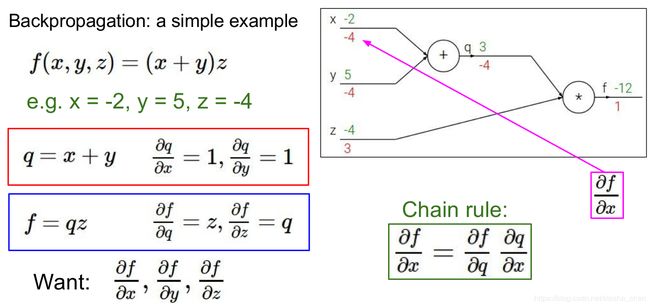
首先举了一个很简单的例子，例子中详细的介绍了前向传播和反向传播的计算方式，其实就是链式法则。每个节点的导数都是用后一个部位的导数乘以当前节点的导数。

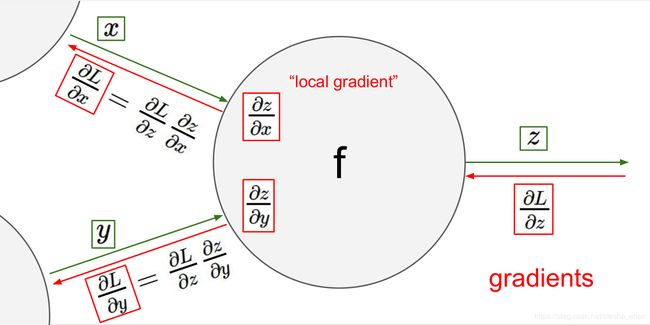
然后总结了一个节点导数的求法，就是上一个节点的导数乘以当前节点的local gradient。

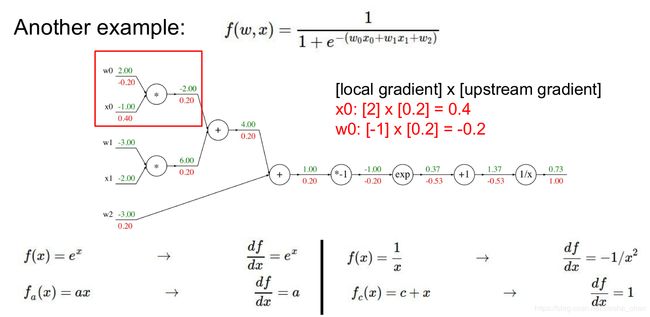
然后举了一个相对复杂的例子，也是一步一步进行了正向和反向传播。

这个例子的公式其实可以看成一个sigmoid函数和一个wx的向量相乘。

最后将链式求导扩展到矩阵的计算

矩阵求导的计算方式也是一样的，需要注意的一个细节是如果，计算需要对进行转置，计算需要对进行转置，并且因为与维度相同，与维度相同，所以我们在计算导数的时候关注一下矩阵维度，这样可以减少错误的概率。

推荐一个补充学习的文章，写的很好CS231n课程笔记翻译：反向传播笔记

几点思考：

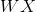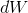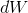1. 神经网络中会用到很多的矩阵相乘，而的值与的值相关，如果的值统一扩大1000倍，那么会变大很多，这样我们就必须用更小的learning_rate，否则收敛效果不好。这就是为什么一般我们都希望的值在一个相对小范围内。
2. 以前我一直不知道tensorflow中是如何进行链式求导的，如果用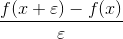进行求导，这样需要进行两次前向计算才能求出导数，所以每次参数更新需要大量的计算。学习了这一课后我知道了框架也是进行的链式求导。比如tensorflow有graph的概念，就是计算图，会将每一个算子也就是op的连接过程记录下来，导数就可以根据计算图和每个op的local gradient公式进行链式求导。op就是一些我们常用的计算，比如加减乘除，relu，softmax，sigmoid，dropout等都是op，他们都有对应的导函数用来求local gradient。

   @ops.RegisterGradient("Relu")
   def _ReluGrad(op, grad):
     return gen_nn_ops.relu_grad(grad, op.outputs[0])

    

作业softmax

作业主要是用循环的方式和向量化的方式实现loss softmax正向和反向传播

1.循环的方式

前向传播很简单，就是套用softmax的公式

代码实现如下：

  num_train = X.shape[0]
  num_cls = W.shape[1]
  for i in range(num_train):
    scores = np.dot(X[i, :], W)
    softmax = np.exp(scores[y[i]]) / np.sum(np.exp(scores))
    loss_log = - np.log(softmax)
    loss += loss_log 

  loss /= num_train
  loss += 0.5 * reg * np.sum(W * W)

反向传播需要计算出，可以用链式法则推导

             (1)

                                                         (2)

            (3)

                                                                                    (4)

公式1是分解后的前向传播，分解成了三个等式

公式2是第一步求导，等同于对求导

公式3是对softmax公式求导，的范围是0到num_cls之间，因为有两种可能行，一个是，这种情况下，可变量既在分子上也在分母上，另一种情况是，这种情况下可变量只在分母上，所以对softmax求导有两个公式。具体的推导过程可以搜一搜，并不难。

公式4是对矩阵相乘求导，，那么，其中是的行，为矩阵的列，所以可以得到公式4.

所以利用循环求导代码如下：

  num_train = X.shape[0]
  num_cls = W.shape[1]
  for i in range(num_train):
    for j in range(num_cls):
      if j == y[i]:
        dW[:, y[i]] += X[i, :] * softmax * (1 - softmax) * (-1 / softmax)
      else:
        softmaxj = np.exp(scores[j]) / np.sum(np.exp(scores))
        dW[:, j] += X[i, :] * (-softmax) * softmaxj * (-1 / softmax)
      
  dW /= num_train
  dW += reg * W

完整的代码如下：

def softmax_loss_naive(W, X, y, reg):
  """
  Softmax loss function, naive implementation (with loops)

  Inputs have dimension D, there are C classes, and we operate on minibatches
  of N examples.

  Inputs:
  - W: A numpy array of shape (D, C) containing weights.
  - X: A numpy array of shape (N, D) containing a minibatch of data.
  - y: A numpy array of shape (N,) containing training labels; y[i] = c means
    that X[i] has label c, where 0 <= c < C.
  - reg: (float) regularization strength

  Returns a tuple of:
  - loss as single float
  - gradient with respect to weights W; an array of same shape as W
  """
  # Initialize the loss and gradient to zero.
  loss = 0.0
  dW = np.zeros_like(W)

  #############################################################################
  # TODO: Compute the softmax loss and its gradient using explicit loops.     #
  # Store the loss in loss and the gradient in dW. If you are not careful     #
  # here, it is easy to run into numeric instability. Don't forget the        #
  # regularization!                                                           #
  #############################################################################
  pass
  num_train = X.shape[0]
  num_cls = W.shape[1]
  for i in range(num_train):
    scores = np.dot(X[i, :], W)
    softmax = np.exp(scores[y[i]]) / np.sum(np.exp(scores))
    lossi = - np.log(softmax)
    loss += lossi
    
    for j in range(num_cls):
      if j == y[i]:
        dW[:, y[i]] += X[i, :] * softmax * (1 - softmax) * (-1 / softmax)
      else:
        softmaxj = np.exp(scores[j]) / np.sum(np.exp(scores))
        dW[:, j] += X[i, :] * (-softmax) * softmaxj * (-1 / softmax)
      
  loss /= num_train
  loss += 0.5 * reg * np.sum(W * W)
  dW /= num_train
  dW += reg * W
  #############################################################################
  #                          END OF YOUR CODE                                 #
  #############################################################################

  return loss, dW

2.向量化

正向传播向量化比较简单

  num_train = X.shape[0]
  num_cls = W.shape[1]
  scores = np.dot(X, W)
  scores_exp = np.exp(scores)
  softmax_all = scores_exp / np.sum(scores_exp, axis=1).reshape((num_train, 1))
  softmax_correct = softmax_all[np.arange(num_train), y]
  loss += np.sum(-np.log(softmax_correct)) / num_train + 0.5 * reg * np.sum(W * W)

反向传播向量化计算的时侯需要注意和保证维度一样

因为上面已经有了两个循环的实现方式，首先去掉第二个循环进行向量化看如何实现。在第二个循环中因为需要区分j和y[i]是否

相等的情况，所以可以使用mask来区分。

pmask = np.zeros((num_cls,)).reshape((num_cls, 1))
pmask[y[i]] = 1.0
nmask = np.abs(pmask - 1.0)

先计算pmask的情况，还是套用上面循环模式下的公式，只不过加上了pmask可以去掉j循环

dW += X[i, :].reshape((num_f, 1)).dot(pmask.T) * softmax_correct * (1 - softmax_correct) * (-1 / softmax_correct)

这个公式可以简化为

dW += X[i, :].reshape((num_f, 1)).dot(pmask.T) * (softmax_correct - 1)

然后计算nmask的情况

dW += X[i, :].reshape((num_f, 1)).dot(nmask.T) * (-softmax_correct) * softmax_all * (-1 / softmax_correct)

可以简化为

dW += X[i, :].reshape((num_f, 1)).dot(nmask.T) * softmax_all

所以去掉一个循环的完整代码是

for i in range(num_train):
	scores = np.dot(X[i, :], W)
	softmax_correct = np.exp(scores[y[i]]) / np.sum(np.exp(scores))

	softmax_all = np.exp(scores) / np.sum(np.exp(scores))
	pmask = np.zeros((num_cls,)).reshape((num_cls, 1))
	pmask[y[i]] = 1.0
	nmask = np.abs(pmask - 1.0)

	dW += X[i, :].reshape((num_f, 1)).dot(pmask.T) * (softmax_correct - 1)
	dW += X[i, :].reshape((num_f, 1)).dot(nmask.T) * softmax_all
  
dW /= num_train
dW += reg * W

然后再去掉最外面的循环就可以简单了，注意一点softmax_correct和softmax_all都是和X的每一行做broadcast相乘，所以向量化的时候也要保留这个计算

pmask = np.zeros((num_train, num_cls))
pmask[np.arange(num_train), y] = 1.0
nmask = np.abs(pmask - 1)

dw += np.dot(X.T, (softmax_correct - 1).reshape(num_train, 1) * pmask)
dW += np.dot(X.T, (nmask * softmax_all))

完全向量化的完整代码如下：

def softmax_loss_vectorized(W, X, y, reg):
  """
  Softmax loss function, vectorized version.

  Inputs and outputs are the same as softmax_loss_naive.
  """
  # Initialize the loss and gradient to zero.
  loss = 0.0
  dW = np.zeros_like(W)

  #############################################################################
  # TODO: Compute the softmax loss and its gradient using no explicit loops.  #
  # Store the loss in loss and the gradient in dW. If you are not careful     #
  # here, it is easy to run into numeric instability. Don't forget the        #
  # regularization!                                                           #
  #############################################################################
  pass
  num_train = X.shape[0]
  num_cls = W.shape[1]
  scores = np.dot(X, W)
  scores_exp = np.exp(scores)
  softmax_all = scores_exp / np.sum(scores_exp, axis=1).reshape((num_train, 1))
  softmax_correct = softmax_all[np.arange(num_train), y]
  loss += np.sum(-np.log(softmax_correct)) / num_train + 0.5 * reg * np.sum(W * W)

  pmask = np.zeros((num_train, num_cls))
  pmask[np.arange(num_train), y] = 1.0
  nmask = np.abs(pmask - 1)
    
  dW += np.dot(X.T, (softmax_correct - 1).reshape(num_train, 1) * pmask)
  dW += np.dot(X.T, (nmask * softmax_all))
    
  dW /= num_train
  dW += reg * W

  #############################################################################
  #                          END OF YOUR CODE                                 #
  #############################################################################

  return loss, dW

 

Neural Networks

学习笔记

这部分的内容很简单，简单介绍了一下神经网络。

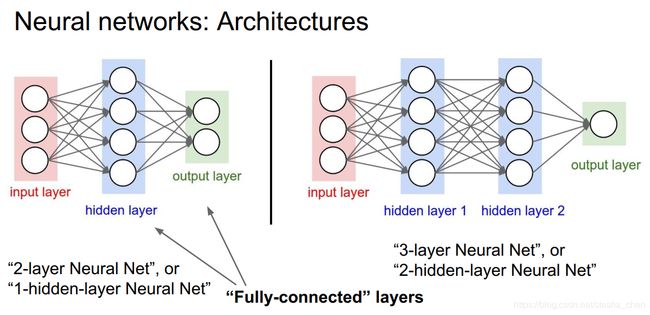
因为之前介绍的都是从输入到输出的模型，如果在中间增加一个隐藏层，就会成为一个输入，一个隐藏层和一个输出层。把这个网络叫做2层神经网络。n层神经网络的n是所有隐藏层加上输出层，输入层不计算在内。

上图就是一个简单的2层神经网络，

如果是三层神经网络就是隐藏层再增加一层

另外如果是2层神经网络也叫做1个隐藏层神经网络，如果是3层神经网络也叫做2个隐藏层神经网络。

如果前一层的所有单元节点和后一层的所有单元节点都连接，就是Fully-connected layers全连接层，现在前面介绍的都是全连接层。

作业two_layer_network

这个作业构建了一个2层的神经网络，需要我们自己实现前向传播，反向传播和梯度下降。由于loss是用softmax进行的计算，所以推导反向传播的公式可以参考前面部分的作业，只是这个作业中多了一层。

前向传播

就是计算loss，公式如下

                                                            

代码实现如下：

    h1 = np.dot(X, W1) + b1
    h1_max = np.maximum(0, h1)
    scores = np.dot(h1_max, W2) + b2

    scores_exp = np.exp(scores)
    softmax_all = scores_exp / np.sum(scores_exp, axis=1).reshape((N, 1))
    softmax_correct = softmax_all[np.arange(N), y]
    loss = - np.sum(np.log(softmax_correct)) / N
    loss += reg * (np.sum(W1 * W1) + np.sum(W2 * W2))

反向传播

可以看出来，如果把换成就是上一节的作业了，所以和很容易求出

    C = b2.shape[0]
    pmask = np.zeros((N, C))
    pmask[np.arange(N), y] = 1.0
    nmask = np.abs(pmask - 1)
    
    dW2 = np.dot(h1_max.T, ((softmax_correct - 1).reshape(N, 1) * pmask))
    dW2 += np.dot(h1_max.T, (softmax_all * nmask))
    db2 = np.dot((softmax_correct - 1), pmask)
    db2 += np.sum(nmask * softmax_all, axis=0)
    
    dW2 /= N
    dW2 += 2 * reg * W2
    db2 /= N  
    grads['W2'] = dW2
    grads['b2'] = db2

接着需要计算和，需要先计算和

的计算其实和是一样的，只是是与相关，而是与相关。其余的式子是一样的

    dh1_max = np.dot(((softmax_correct - 1).reshape(N, 1) * pmask), W2.T)
    dh1_max += np.dot((softmax_all * nmask), W2.T)
    dh1_max /= N

接着计算，公式如下

    hmask = (h1 > 0)
    hmask = hmask.astype(np.int32)
    dh1 = dh1_max * hmask

接着再计算和就非常容易了

    dW1 = np.dot(X.T, dh1) + 2 * reg * W1
    db1 = np.sum(dh1, axis=0)

这样所有参数的导数都计算出来了。

梯度下降

梯度下降就是根据参数的导数和learning_rate来更新参数，代码如下

      W1 -= learning_rate * grads['W1']
      W2 -= learning_rate * grads['W2']
      b1 -= learning_rate * grads['b1']
      b2 -= learning_rate * grads['b2']

这样所有主要的内容就实现了。

小结：

通过这个课程的学习可以比较清晰的实现前向和反向传播，虽然框架能帮我们实现这些功能，但是自己推导对于理解网络参数的相互关系还是非常有帮助的。