三维重建之DLT method

1 基本概念

我们的目标是，首先在真实世界中选取特定的点，测量其坐标（这个是人为可以测量得到的），然后观察它在图像中的坐标，估计相机的内、外参数，利用相机的内外参数，就可以计算真实世界中任意点的坐标。

2 引言

我们使用摄像机对物体进行拍摄时，本质上是将object space中的点$O$映射到film plane中的图像点$I^{\prime }$上，具体关系如图1a所示；而数字化的又是将图上的点再次映射到projection plane$I$上，具体关系如图1b所示。

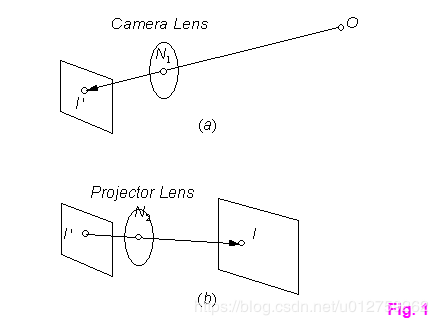
但是通常情况下，为了简单起见，人们一般都是将object space与projection plane相对应，也就是object space中的$O$点直接映射到projection plane中的$I$上。

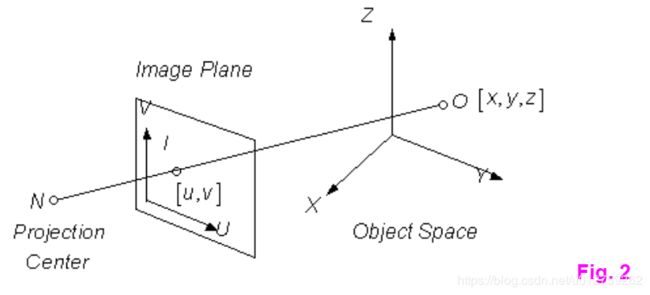
在上图中，可以明显的看到，object space中的坐标系$XYZ$-system 和 image-plane中的$UV$-system，$N$是project center，在上图中，点$I$和点$O$存在映射关系，假设点$I,N,O$，这三个点之间的关系满足colinear（共线性），这也是DLT method成立的基础。

3. 具体算法

3.1 2D DLT method

3.1.1 算法思想

假设project center(N)在object-space中的位置坐标为$[x_o,y_o,z_o]$，那么，$O,N$之间向量表示为：$A=[x-x_o,y-y_o,z-z_o]$

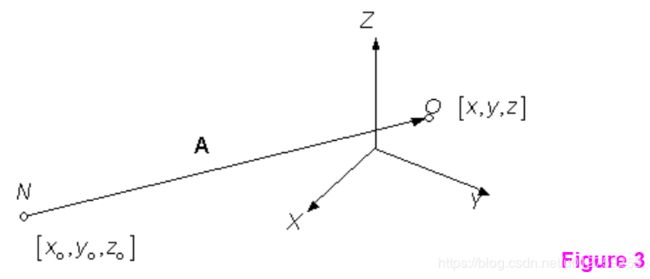
由于在image plane上面只有$UV$两个坐标系，这个时候我们再加一个轴$W$作为第三个轴，构成立体结构，那么，在image plane空间中，$W$方向上的坐标永远为0，那么坐标可以表示为：

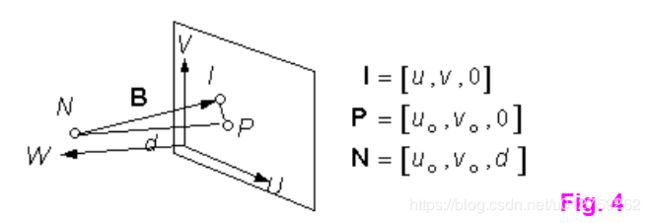
对于新点$P$，记为principal point，那么，$NP$平行于轴$W$，垂直于面image plane，又称为principal axis，$NP$的距离称为principal distance，长度为$d$，假设$P$的坐标为$[u_o,v_o,0]$，而$N$的坐标为$[u_o,v_o,d]$，那么$B$可表示为$[u-u_o,v-v_o,-d]$。

由于$O,I,N$是共线的，那么向量$A$和$B$之间的关系为
$$B=cA$$
上式中，$c$是一个比例因子，为了方便计算，可将$A$用image-plane进行表示，假设image plane与object plane之间的变换矩阵为：

在上式中，$A^{(I)}$代表在image-plane中的$A$（也就是$IP$），$A^{(O)}$代表在object-plane中的$A$，$T_{I/O}$代表从object-plane到image-object空间的变换矩阵。于是向量$B$与向量$NO$之间就有关系式：

或者可以表示为：

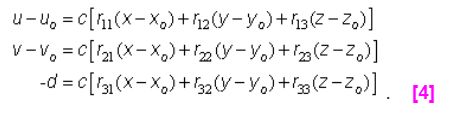
根据公式4的第三个分量，可以计算出比例因子$c$为：

于是前两个分量可以表示为：

注意一点：$u,v,u_o,v_o$代表的是真实生活中照片上的距离单位可能是cm，而映射到digitization system中可能使用不同的长度单位，如像素，因此，必须再乘除比例因子：$\lambda$

这里的${\lambda }_u$和${\lambda }_v$是两个方向的比例，一般来说不会一样。现在，整理$x,y,z$的表达式，

其中，


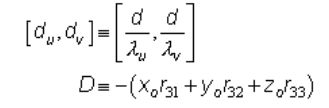
系数$L_1$到$L_{11}$代表了object plane和image-plane的映射关系。

3.1.2 求解参数

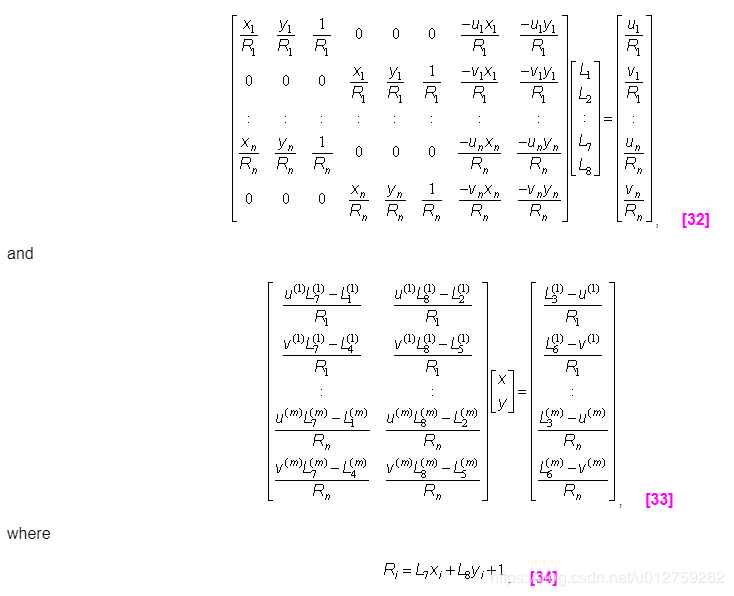
由于是在2D图像中（比如俯拍），真实世界的$z$轴总是为0，那么，$u,v$的表达式可以表示成（系数与公式8不是一个东西）

根据公式31，设置至少$n$个坐标点$n\ge 4$，和至少$m$个相机$m\ge 1$，变换矩阵可以得到：