开放的多点贝赛尔曲线实现
初识贝塞尔曲线
在实现开放的多点贝塞尔曲线之前,我们先了解下贝塞尔曲线的一些基本的知识.后面链接解释的蛮详细的:
贝塞尔曲线初探
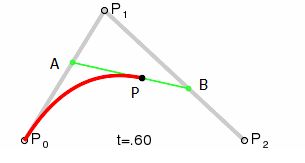
链接文章中,我们看以清楚的看出贝塞尔曲线的绘制过程.下面就简单说下二阶的绘制原理.如下图所示:
P0A/P0P1 = P1B/P1P2 = AP/AB = t ( 0<=t<=1)
随着t的值从0-1变化P点位置就是我们所要的贝塞尔点集
从上面的过程可以得出一下几点:
1. 贝塞尔点数量可以用t等分的数量控制
2. 贝塞尔点分布不是均匀的(要做匀速的话,要对生成的点集在做处理,这里我们不考虑)
3. 贝塞尔曲线起始与P0P1相切,结束与P1P2相切(这个就是实现多点贝塞尔的关键所在)
多点贝塞尔曲线实现思路
根据上面第3点,只要前一段贝塞尔曲线结束点的切线与下一段贝塞尔曲线起始点的切线重合.这样两段贝塞尔曲线就可以平滑连接.
现在的关键在于计算贝塞尔曲线控制点的位置,这里我们用的是三阶的贝塞尔曲线
三阶贝塞尔曲线控制点计算
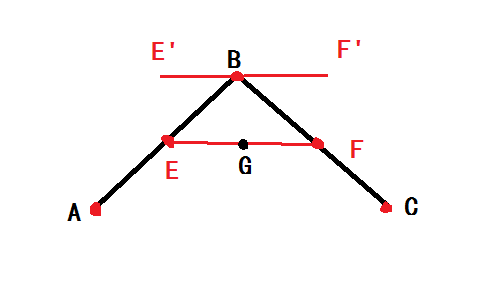
- 取AB,BC中点E,F:
lua:
local EPos = ccpMidpoint(APos,BPos)
local FPos = ccpMidpoint(BPos,CPos)
- E,F平移到E',F' G与B重合
lua:
-- 平移向量
local GB_Vec = ccpSub(BPos,ccpMidpoint(EPos,FPos))
-- 平移点
local controlP1 = ccpAdd(GB_Vec,EPos)
local controlP2 = ccpAdd(GB_Vec,FPos)
- E',F' 基本可以作为控制点,为了调整曲线效果可以将E',F'往B方向收缩或扩大(以下是向外扩展0.4倍)
lua:
controlP1 = ccpAdd(ccpMult(ccpSub(BPos,controlP1),-0.4),controlP1)
controlP2 = ccpAdd(ccpMult(ccpSub(BPos,controlP2),-0.4),controlP2)
- 绘制三次贝塞尔曲线贝塞尔,controlP = {起始点,控制点1,控制点2,结束点}
lua:
function M:bezier3func(uu, controlP)
local part1 = ccpMult(controlP[1],uu*uu*uu)
local part2 = ccpMult(controlP[2],3*uu*uu*(1-uu))
local part3 = ccpMult(controlP[3],3*uu*(1-uu)*(1-uu))
local part4 = ccpMult(controlP[4],(1-uu)*(1-uu)*(1-uu))
return ccpAdd(ccpAdd(part1,part2),ccpAdd(part3,part4))
end
以上实现思路来源于穿过已知点画平滑曲线(3次贝塞尔曲线)
代码实现
lua:
-- 传入节点node
-- 多点开放贝塞尔曲线
function M:bezierSceneMove(node)
self:updateFishData(node)
-- 取中点
local midPos1 = ccpMidpoint(node.myPos,node.nextPos)
local midPos2 = ccpMidpoint(node.nextPos,node.endPos)
-- 平移向量
local dPos = ccpSub(node.nextPos,ccpMidpoint(midPos1,midPos2))
-- 中点平移
local controlP1 = ccpAdd(dPos,midPos1)
local controlP2 = ccpAdd(dPos,midPos2)
-- 控制点计算
controlP1 = ccpAdd(ccpMult(ccpSub(node.nextPos,controlP1),-0.4),controlP1)
controlP2 = ccpAdd(ccpMult(ccpSub(node.nextPos,controlP2),-0.4),controlP2)
local totalDis = 0
local lastP = self:bezier3func(0,{node.myPos,node.lastContrlP,controlP1,node.nextPos})
for i=0,100 do
local pos = self:bezier3func(i/100,{node.myPos,node.lastContrlP,controlP1,node.nextPos})
totalDis = totalDis + ccpDistance(lastP,pos)
lastP = pos
end
local totleTimes = math.floor(totalDis/node.speed*60)
local tag = totleTimes
self.moveAction = A.cycle({
{"delay",1/60},
{"fn",function( ... )
local pos = self:bezier3func(tag/totleTimes,{node.myPos,node.lastContrlP,controlP1,node.nextPos})
local angle = 180-CC_RADIANS_TO_DEGREES(ccpToAngle(ccpSub(pos,node:point())))
if angle ~= 180 then
node:rotation(angle)
end
node:setPosition(pos)
tag = tag - 1
if tag < 0 then
self:stopAction(self.moveAction)
node.lastContrlP = controlP2
self:bezierSceneMove(node)
end
end},
}):at(self)
end
-- 更新下一个点
function M:updateFishData(node)
if node.myPos == nil then
node.myPos = node:point()
node.nextPos = ccp(N.random(40,900),N.random(40,600))
node.endPos = ccp(N.random(40,900),N.random(40,600))
node.lastContrlP = ccpAdd(node:point(),ccp(100,0))
local angle = 180-CC_RADIANS_TO_DEGREES(ccpToAngle(ccpSub(node.nextPos,node:point())))
node:rotation(angle)
else
node.myPos = node.nextPos
node.nextPos = node.endPos
node.endPos = ccp(N.random(40,900),N.random(40,600))
-- 随机点位过近/折返
-- while ccpDistance(node.endPos,node.nextPos) < 200 or CC_RADIANS_TO_DEGREES(ccpAngle(ccpSub(node.myPos,node.nextPos),ccpSub(node.endPos,node.nextPos))) < 40 do
-- node.endPos = ccp(N.random(40,900),N.random(40,600))
-- end
end
node.speed = N.random(140,160)
end
--三次贝塞尔曲线 X
function M:bezier3func(uu, controlP)
local part1 = ccpMult(controlP[1],uu*uu*uu)
local part2 = ccpMult(controlP[2],3*uu*uu*(1-uu))
local part3 = ccpMult(controlP[3],3*uu*(1-uu)*(1-uu))
local part4 = ccpMult(controlP[4],(1-uu)*(1-uu)*(1-uu))
return ccpAdd(ccpAdd(part1,part2),ccpAdd(part3,part4))
end