MPT的全称是Merkle Patricia Tree, 从这里可以看出MPT是Merkle Tree + Patricia Tree。接下来就来讲讲这两种树:
Merkle Tree
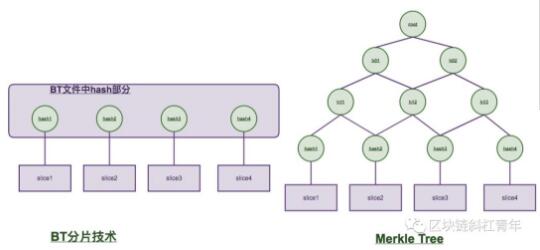
区块链P2P网络中,如果需要传输的数据很大,就需要同时从多个机器上下载数据,而且很可能有些机器是不稳定(可能下载速度很慢)或者不可信的(需要重新下载)。为了快速下载大块数据并验证,更好的办法是把大文件分割成小的数据块(例如把大文件分割成4K为单位的小数据块)。这样的好处是如果小块数据在传输过程中损坏了或者是错误的数据,那么只要重新下载这一块数据就行了,不用重新下载整个文件。
由于只有大文件内容的hash, 当其中一块小数据错误时,我们是能检出由小块数据拼凑出来的大数据是错误的,但是我们不知道哪块小数据是错误的,就没法通过重传错误的小数据来纠正。哪怎么处理呢?为每个小块生成hash, 节点先把小块数据的hash都下载下来,然后就可以一个一个验证小块数据是否正确了。那问题又来了,小块数据的hash的正确性谁来保证呢?这个由信任节点来保证,比如BT论坛上的bt种子文件,这个种子文件就记录了原始文件的小块数据的hash. 验证问题解决了,但是多出来了很多小块数据hash,当数据很大时,这个hash数据量也不小。因而Merkle Tree出来了,它可以解决这个问题。
小块数据的hash两两组合再次生成新的hash,然后新生成的hash又两两合并生成更新的hash,直至最后两个hash生成一个hash root,这个叫merkle root(默克尔根)。可见merkle tree和传统bt分片技术只是对小块数据hash的组织方式不一样。参考以太坊:www.300gu.com
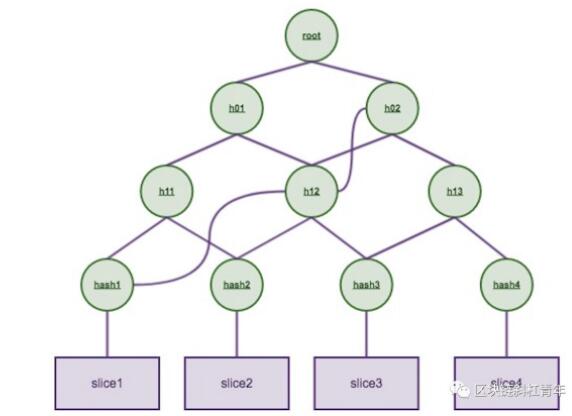
看到上面的图,你可能会说,merkle tree不是生成更多hash数据了啊,怎么能降低数据传输量。确实,对于数据发送方来说,相比传统分片技术,它是需要保存完整merkle tree, 会多占用一点空间。但是对于接受方来说,它在验证某一块数据不需要下载全部hash,只需一段merkle 路径即可,比如下图中的hash1, h12, h02这3个hash
如果要验证slice2数据的正确性,只需要拿到hash1, h12, h02这3个hash再加上本地存储的root hash,就可以验证了。需要传输的hash数据量从n变为log2n.
Patricia Tree
patricia tree 前缀树,是一种编码方式,它是传统trie的改进。
Trie树
Trie,又称前缀树或字典树,是一种有序树状的数据结构,其中的键通常是字符串,常用语存储Key-value数据结构。
Trie与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,节点对应的key是根节点到该节点路径上的所有节点key值前后拼接而成,节点的value值就是该key对应的值。根节点对应空字符串key。
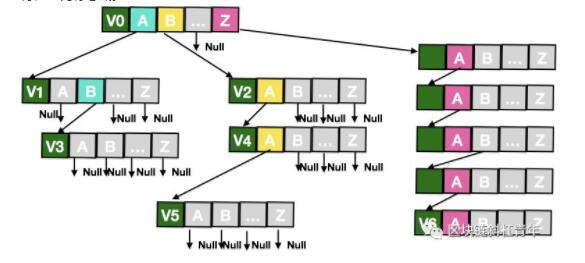
如果key是英文单词,trie的每个节点就是一个长度为27的指针数组,index0-25代表a-z字符,26为标志域。
上面的存储的数据如下:
[‘A’] = V1, [‘AB’] = V3, [‘B’] = V2, [‘BA’] = V4, [‘BAA’] = V5, [‘ZAABA’] = V6
从上面可以看出ZAABA这个key,没有和任何其他key共享字段,但是却产生了6层,这种无用的深度增加有什么方法减少吗?Patricia Tree就可以解决这个问题
Merkle Patricia Tree对trie的改进
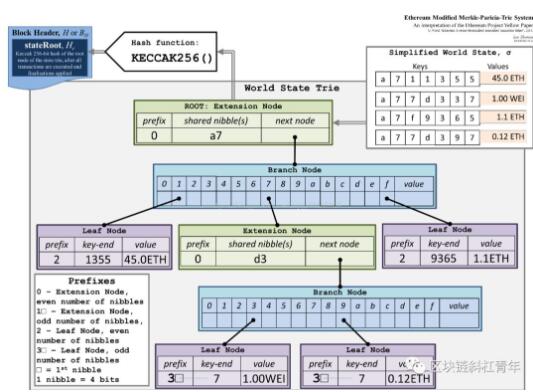
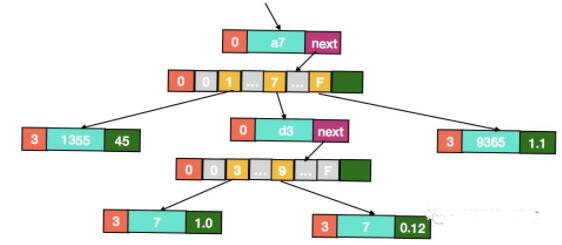
上面tries出现的问题的根本原因是每个前置节点只能表示一个字母,key有多长,树的深度就会多长,不管这个key有没有和其他key共享部分key。因而允许一个节点表示变长的key就可以解决这个深度,具体以官方的下图为例:
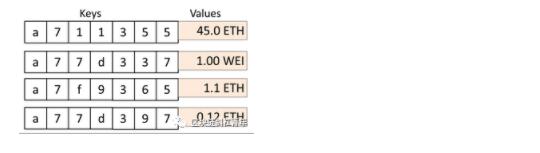
上图存储的key-value如下:
从前面结构图可以看出,Merkle Patricia Tree有4种类型的节点:
叶子节点(leaf),表示为[key,value]的一个键值对。和前面的英文字母key不一样,这里的key都是16编码出来的字符串,每个字符只有0-f 16种,value是RLP编码的数据
扩展节点(extension),也是[key,value]的一个键值对,但是这里的value是其他节点的hash值,通过hash链接到其他节点
分支节点(branch),因为MPT树中的key被编码成一种特殊的16进制的表示,再加上最后的value,所以分支节点是一个长度为17的list,前16个元素对应着key中的16个可能的十六进制字符,如果有一个[key,value]对在这个分支节点终止,最后一个元素代表一个值,即分支节点既可以搜索路径的终止也可以是路径的中间节点。分支节点的父亲必然是extension node
空节点,代码中用null表示
原理解释
插入第一个
接着插入a77d337,由于和a711355共享前缀’a7’,因而可以创建’a7'扩展节点。
接着插入a7f9365,也是共享’a7’,只需新增一个leaf node.
最后插入a77d397,这个key和a77d337共享’a7’+’7d’,因而再需要创建一个’7d’扩展节点