广义线性模型--Generalized Linear Models

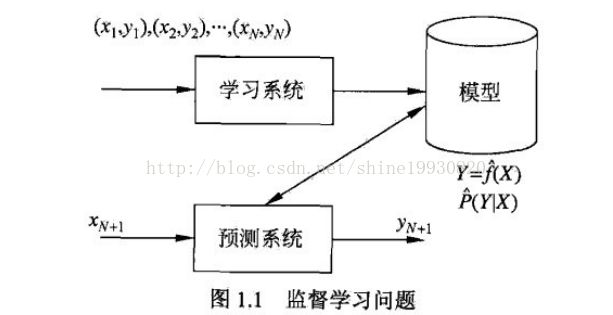
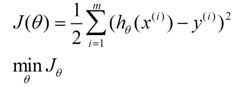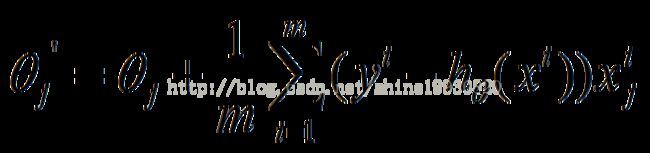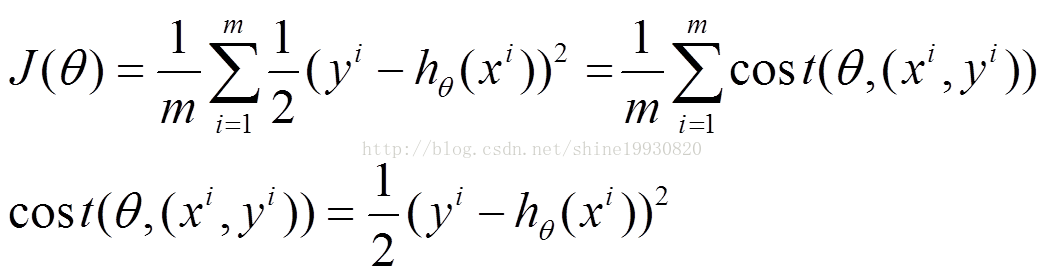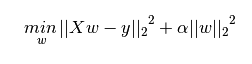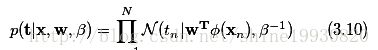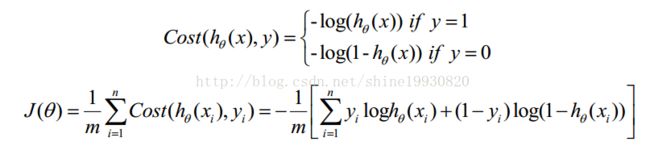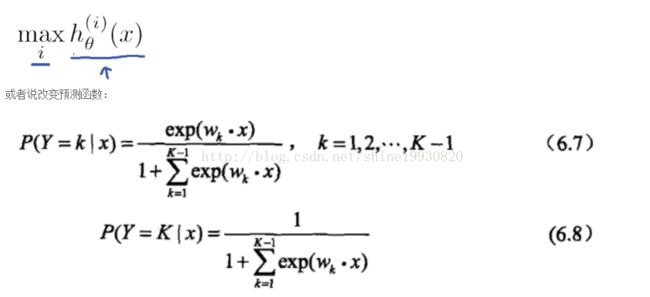监督学习问题：

1、线性回归模型：

适用于自变量X和因变量Y为线性关系

2、广义线性模型：

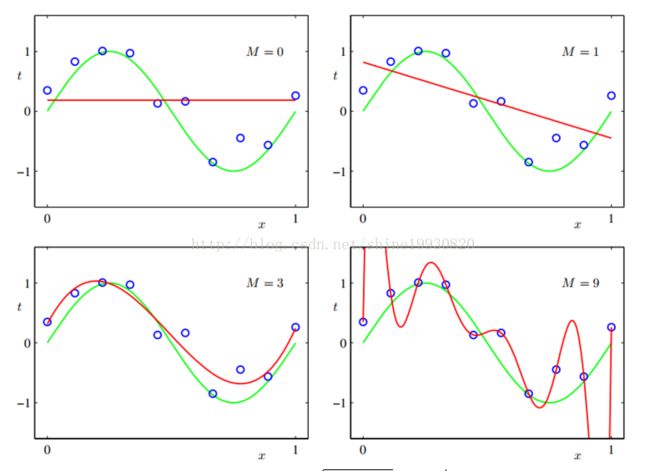
对于输入空间一个区域改变会影响所有其他区域的问题，解决为：把输入空间划分成若干个区域，然后对每个区域用不同的多项式函数拟合

是为了克服线性回归模型的缺点出现的，是线性回归模型的推广。

首先自变量可以是离散的，也可以是连续的。离散的可以是0-1变量，也可以是多种取值的变量。

与线性回归模型相比较，有以下推广：

根据不同的数据，可以自由选择不同的模型。大家比较熟悉的Logit模型就是使用Logit联接、随机误差项服从二项分布得到模型。

回归的线性模型

对于输入空间一个区域改变会影响所有其他区域的问题，解决为：把输入空间划分成若干个区域，然后对每个区域用不同的多项式函数拟合

Polynomial Curve Fitting

为神马不是差的绝对值？请看下面分解：

当我们寻找模型来拟合数据时，偏差是不可避免的存在的。对一个拟合良好的模型而言，这个偏差整体应该是符合正态分布的，

根据贝叶斯定理：P(h|D)=P(D|h)*P(h)/P(D)

    即P(h|D)∝P(D|h)*P(h) (∝表示“正比于”)

    结合前面正态分布，我们可以写出这样的式子：实际纵坐标为 Yi 的点 (Xi, Yi) 发生的概率 p(di|h)∝ exp(-(ΔYi)^2)

各个数据点偏差是独立的，所以可以把每个概率乘起来。于是生成 N 个数据点的概率为 EXP[-(ΔY1)^2] * EXP[-(ΔY2)^2] * EXP[-(ΔY3)^2] * .. = EXP{-[(ΔY1)^2 + (ΔY2)^2 + (ΔY3)^2 + ..]} 最大化这个概率就是要最小化 (ΔY1)^2 + (ΔY2)^2 + (ΔY3)^2 + .. 。得解！

正态分布的概率密度函数是欧拉数的幂函数形式。并不是所有的模型都可以有最优解，有些只有局部最优，有些则压根找不到，例如NPC问题。绝对值的和无法转化为一个可解的寻优问题，既然无法寻优如何得到恰当的参数估计呢？

x(i)的估计值与真实值y(i)差的平方和作为错误估计函数，前面乘上的1/2是为了在求导的时候，这个系数就不见了。如何调整θ以使得J(θ)取得最小值有很多方法：

1. 梯度减少的过程：

对于我们的函数J(θ)求偏导J：

下面是更新的过程，也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值，-后面的部分表示按梯度方向减少的量，α表示步长，也就是每次按照梯度减少的方向变化多少。

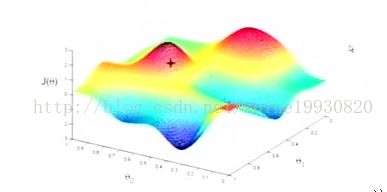
对于一个向量θ，每一维分量θi都可以求出一个梯度的方向，我们就可以找到一个整体的方向，在变化的时候，我们就朝着下降最多的方向进行变化就可以达到一个最小点，不管它是局部的还是全局的。

梯度下降法是按下面的流程进行的：

1）首先对x 赋值，这个值可以是随机的，也可以让x是一个全零的向量。

2）改变x 的值，使得f(x)按梯度下降的方向进行减少。

3）循环迭代步骤2，直到x的值变化到使得f(x) 在两次迭代之间的差值足够小，比如0.00000001，也就是说，直到两次迭代计算出来的f(x) 基本没有变化，则说明此时f(x) 已经达到局部最小值了。

• 靠近极小值时收敛速度减慢。
• 直线搜索时可能会产生一些问题。
• 可能会“之字形”地下降。

• 这个算法将会在很大的程度上被初始点的选择影响而陷入局部最小点

1、批量梯度下降的求解思路如下：

（1）将J(theta)对theta求偏导，得到每个theta对应的的梯度

   

（2）由于是要最小化风险函数，所以按每个参数theta的梯度负方向，来更新每个theta

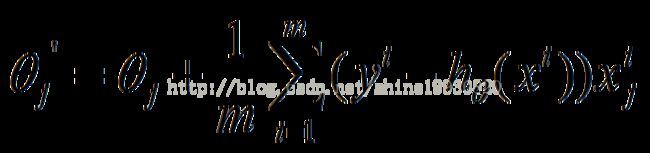
（3）从上面公式可以注意到，它得到的是一个全局最优解，但是每迭代一步，都要用到训练集所有的数据，如果m很大，那么可想而知这种方法的迭代速度！！所以，这就引入了另外一种方法，随机梯度下降。

2、随机梯度下降的求解思路如下：

（1）上面的风险函数可以写成如下这种形式，损失函数对应的是训练集中每个样本的粒度，而上面批量梯度下降对应的是所有的训练样本：

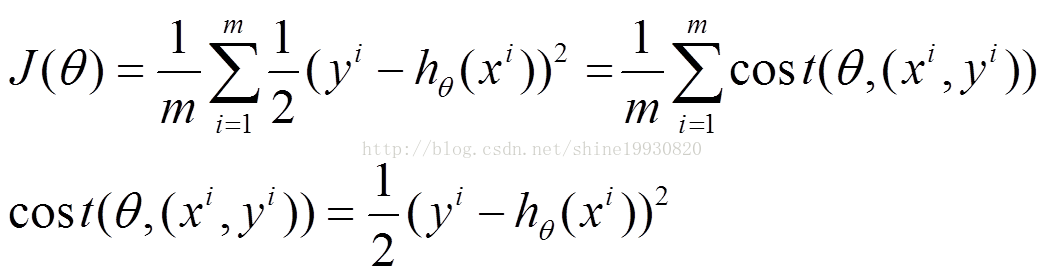
（2）每个样本的损失函数，对theta求偏导得到对应梯度，来更新theta

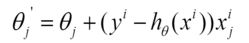
（3）随机梯度下降是通过每个样本来迭代更新一次，如果样本量很大的情况（例如几十万），那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

对于上面的linear regression问题，最优化问题对theta的分布是unimodal，即从图形上面看只有一个peak，所以梯度下降最终求得的是全局最优解。然而对于multimodal的问题，因为存在多个peak值，很有可能梯度下降的最终结果是局部最优。

一个衡量错误的指标是root mean square error：

过拟合的解决办法，目前讲了三点：

1. 增加训练数据集合
2. 加入本书的"万金油" 贝叶斯方法
3. 加入regularization。

Regularization

control the over-fitting phenomenon

参数w对训练数据的变化异常敏感，尽可能的去捕捉这个变化(使误差最小)，而他捕捉的方式，就是肆意改变自身的大小，而不管训练数据的大小(向量w的各个值会正负抵消，而得出一个和目标变量相当的输出)。这是模型的缺陷，也是过拟合的元凶。

而引入正则化项之后，向量w想要变大自身并正负抵消来拟合目标时，|w|会变的非常大，与目标变量相去甚远，过拟合的阴谋失败了。

Ordinary Least Squares

fits a linear model with coefficients W to minimize the residual sum of squares between the observed responses in the dataset, and the responses predicted by the linear approximation. Mathematically it solves a problem of the form:

However, coefficient estimates for Ordinary Least Squares rely on the independence of the model terms.

Ordinary Least Squares Complexity

X is a matrix of size (n, p) this method has a cost of , assuming that n>=p.

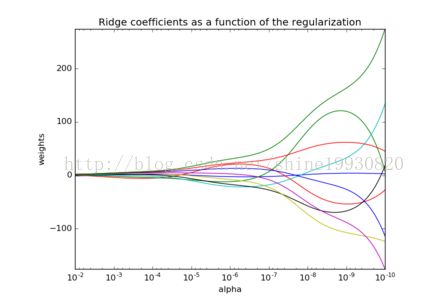
 Ridge Regression 岭回归

regression addresses some of the problems of Ordinary Least Squares by imposing a penalty on the size of coefficients. The ridge coefficients minimize a penalized residual sum of squares,

Here,  is a complexity parameter that controls the amount of shrinkage: the larger the value of , the greater the amount of shrinkage and thus the coefficients become more robust to collinearity.

参数值和alpha的变化关系。

ax.set_color_cycle(['b','r','g','c','k','y','m'])

Bayesian Regression

最大似然估计中很难决定模型的复杂程度，ridge回归加入的惩罚参数其实也是解决这个问题的，同时可以采用的方法还有对数据进行正规化处理，另一个可以解决此问题的方法就是采用贝叶斯方法。

目标变量t的取值是由一个deterministic function y(x,w)和一个高斯噪声共同决定的，如3.7式：

目标值t的概率分布可以写成3.8： 

这里的x是向量，是一个更普适的表达。式3.8的含义是，t取某个值的概率，是均值为y(x,w)，precision为beta的正态分布。

选择二阶损失函数，t的预测就是条件数学期望 E(t|x): 

高斯噪声没有了。

以上，敲定了本问题的概率模型，接下来给出似然函数并用最大似然求解。 用X表示所有的向量x, X={x1....xN}，他们分别对应向量t的t1....tN，在观测点独立同分布的前提下，式3.8可以对所有向量t和向量x写成 ：

    这就是likelihood function，后续还会经常用到。与前面一样，我们最大化这个似然函数：对这个式子两边求ln，然后令x偏导数为0，求得拐点的位置，也就求得了w的表达式。

    与普通的线性回归比较，likelyhood function p(t|x,w)是一致的。不同的是：参数w，一个是确定的，一个是概率分布；对最终结果t的预测，一个是通过损失函数来决定，一个是在w的空间上积分。

高斯噪声假设下，p(t|x)是unimodal(单峰，有一个极大值)的，这可能与事实不符。而混合条件高斯分布，它会允许multimodal。

贝叶斯回归方法有三个关键点：

1. 求概率分布p(W|D). 

2. 求likelyhood p(t|x,W) . 

3. 在w空间上积分(1.68)。

在我们未观测到数据集D之前，可以先假设w服从均值为m0，方差为S0的高斯分布：

w的后验概率与似然函数和先验概率的乘积成正比。因为w的先验概率是高斯分布，所以共轭的后验概率也是高斯分布(高斯likelyhood=>高斯先验w=>高斯后验w)。

已知数据x和t， w的后验概率为3.49：

Phi 自变量x的特征组成的矩阵。

w的先验在负无穷正无穷上均匀分布时，贝叶斯线性回归就蜕化成了普通的线性回归。普通线性回归并不认识w是一个概率分布，就是在所有的可能性下，直接求解似然函数。

对于先验概率的选择，有更加泛化的表示，如公式3.56。为了简化问题，我们看一个w先验概率为： 均值为0，方差为alpha倒数的高斯分布：

看这两个式子，Phi和T都来自观测数据，待定参数只有alpha和beta。

把这个后验分布写成具体的概率密度函数，然后对它的w求log，就得到了

相似于λ = α/β 时的ridge regression

贝叶斯视角下的模型选择

对于一个问题、一个数据集，可能会有多个模型与之对应，每个模型都会以一定概率生成这个数据集，那么我们选择哪一个模型呢？按照以前的做法，我可能会说选择概率最大的那个呗。

如果我们有一个数据集D,有L个模型 Mi，i=1,....L，我们感兴趣的是给定数据D，选择某个Mi的后验概率如3.66:

给定x，对于t的预测可以用3.67来表示：

Logistic regression

Logistic回归与多重线性回归实际上有很多相同之处，最大的区别就在于它们的因变量不同，可以归于同一个家族，即广义线性模型（generalizedlinear model）。

如果是连续的，就是多重线性回归； 如果是二项分布，就是Logistic回归； 如果是Poisson分布，就是Poisson回归； 如果是负二项分布，就是负二项回归。

Logistic回归主要在流行病学中应用较多，比较常用的情形是探索某疾病的危险因素，根据危险因素预测某疾病发生的概率，等等。例如，想探讨胃癌发生的危险因素，可以选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否胃癌，即“是”或“否”，自变量就可以包括很多了，例如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的，也可以是分类的。

常规步骤

Regression问题的常规步骤为：

1. 寻找h函数（即hypothesis）；
2. 构造J函数（损失函数）；
3. 想办法使得J函数最小并求得回归参数（θ）

构造预测函数h

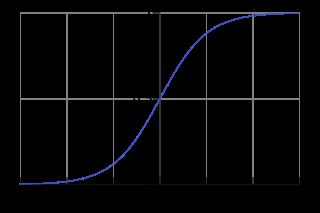
Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别），所以利用了Logistic函数（或称为Sigmoid函数），函数形式为：

Sigmoid 函数在有个很漂亮的“S”形;

 

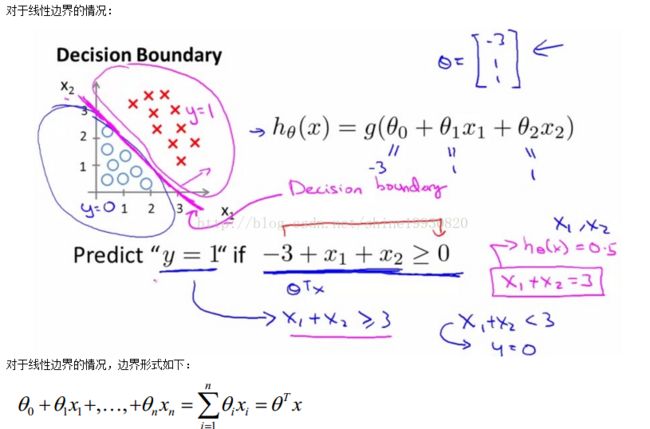
决策边界分为线性和非线性.

对于线性边界的情况:

构造损失函数J

Cost函数和J函数如下，它们是基于最大似然估计推导得到的。

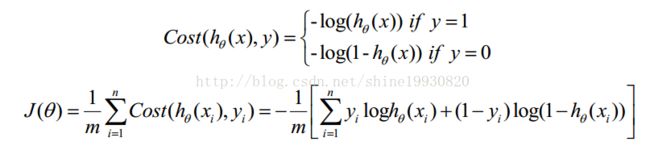
下面详细说明推导的过程：

（1）式综合起来可以写成：

因为乘了一个负的系数-1/m，所以取J(θ)最小值时的θ为要求的最佳参数。

梯度下降法求的最小值

 

一个二维logistic regression的例子：

One-vs-all(one-vs-rest):

对于多类分类问题，可以将其看做成二类分类问题：保留其中的一类，剩下的作为另一类。

总结-One-vs-all方法框架：

对于每一个类 i 训练一个逻辑回归模型的分类器h(i)θ(x)，并且预测 y = i时的概率；

对于一个新的输入变量x, 分别对每一个类进行预测，取概率最大的那个类作为分类结果：

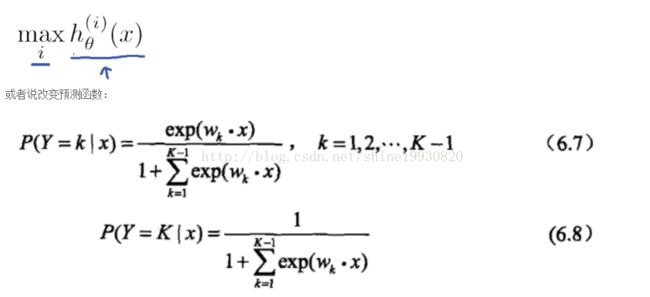
CSDN博客原文

http://blog.csdn.net/shine19930820/article/details/50997645

授人以鱼不如授人以渔：

python sklearn数据预处理：

http://blog.csdn.net/shine19930820/article/details/50915361

交叉验证的Java weka实现，并保存和重载模型

http://blog.csdn.net/shine19930820/article/details/50921109

http://ruqiang.me/blog/2013/08/06/linearregression-2-bayesianlinearregression/

http://ruqiang.me/blog/2013/07/31/linearregression-1-overview/

http://blog.csdn.net/dark_scope/article/details/8558244

http://www.tuicool.com/articles/auQFju

http://blog.csdn.net/zouxy09/article/details/20319673

转载于:https://www.cnblogs.com/aaronchou820/p/6696253.html