均匀的生成圆和三角形内的随机点

代码在每一章节最后

 

一、均匀生成圆内的随机点

我们知道生成矩形内的随机点比较容易，只要分别随机生成相应的横坐标和纵坐标，比如随机生成范围[-10,10]内横坐标x，随机生成范围[-20,20]内的纵坐标y，那么(x,y)就是生成的随机点。由此，我们很容易的想到了算法1

算法1（正确的）：

每个圆对应一个外切矩形，我们随机生成矩形内的点，如果该点在圆内，就返回改点，否则重新生成直到生成的点在圆内。

该方法的缺点是有可能连续几次都生成不了符合要求的点。（可以求得：每次生成点时，该点有 的概率在圆内）

 

算法2（错误的）：

可能有的人想到该方法，根据圆的解析式 （假设圆心在原点）我们可以先随机生成[-R, R]范围内横坐标x，然后生成 范围内的随机数y，(x,y)就是需要的点。

我们写程序模拟了该过程，从下图可以看出，我们可以看到当x靠近圆的边缘使，y的范围减小，因此两边边缘的点较密集，靠近圆心的点较稀疏。

 

算法3（错误的）：

还可以根据极坐标，圆内的点可以如下描述

x = r*sin(theta)

y = r*cos(theta)

其中0 <= r <= R, 0 <= theta < 360

先随机生成[0, 360)内的theta，然后随机生成[0, R]内的r。

theta固定后，当r越靠近R，即点越靠近圆的边缘，因此如果r是[0，R]等概率生成的，那么圆的边缘的点会比靠近圆心处要稀疏。

算法4（正确的）：

和算法3一样还是根据极坐标

x = r*sin(theta)

y = r*cos(theta)

其中0 <= r <= R, 0 <= theta < 360                      本文地址

先随机生成[0, 360)内的theta，然后随机生成[0, 1]内的k, 且r = sqrt(k)*R。

根据根号函数的性质，这样使得r的分布在k靠近1（靠近边缘）的地方点变得较密，具体证明可参考here, 也可以参考论文“矩形和椭圆内均匀分布随机点定理及应用”，圆是椭圆的特例

以上的4个算法的代码如下(Python3.3):

import numpy as np
import matplotlib.pyplot as plt
import random
import math

#博客算法1
def GeneratePointInCycle1(point_num, radius):
    for i in range(1, point_num+1):
        while True:
            x = random.uniform(-radius, radius)
            y = random.uniform(-radius, radius)
            if (x**2) + (y**2) < (radius**2):
                break
        plt.plot(x, y, '*', color = "black")

#博客算法2
def GeneratePointInCycle2(point_num, radius):
    for i in range(1, point_num+1):
        x = random.uniform(-radius, radius)
        y_max = math.sqrt(radius**2 - x**2)
        y = random.uniform(-y_max, y_max)
        plt.plot(x, y, '*', color = "black")

#博客算法3
def GeneratePointInCycle3(point_num, radius):
    for i in range(1, point_num+1):
        theta = random.random()*2*pi;
        r = random.uniform(0, radius)
        x = r*math.sin(theta)
        y = r*math.cos(theta)
        plt.plot(x, y, '*', color = "black")

#博客算法4
def GeneratePointInCycle4(point_num, radius):
    for i in range(1, point_num+1):
        theta = random.random()*2*pi;
        r = random.uniform(0, radius)
        x = math.sin(theta)* (r**0.5)
        y = math.cos(theta)* (r**0.5)
        plt.plot(x, y, '*', color = "black")      


pi = np.pi
theta = np.linspace(0, pi*2, 1000)
R = 1
x = np.sin(theta)*R
y = np.cos(theta)*R

plt.figure(figsize=(6,6))
plt.plot(x,y,label = "cycle",color="red",linewidth=2)
plt.title("cycyle")
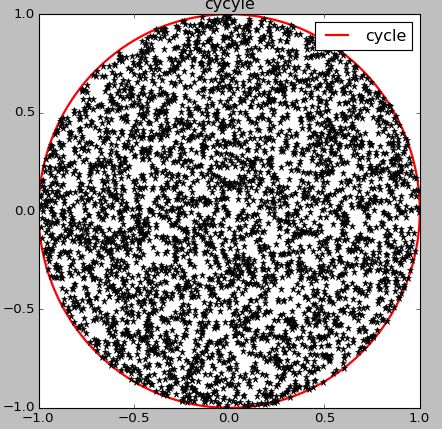
GeneratePointInCycle4(4000, R) #修改此处来显示不同算法的效果
plt.legend()
plt.show()

---

一、均匀生成三角形内的随机点

算法5（错误的）

对于三角形ABC和一点P，可以有如下的向量表示：

p点在三角形内部的充分必要条件是：1 >= u >= 0, 1 >= v >= 0, u+v <= 1。

先生成[0,1]的随机数u，然后生成[0, 1-u]内的随机数v，u、v生成后，就可以得到p点的坐标:

由下图可知，该算法生成的点在靠近A点处较浓密

 

算法6（正确的）

如图所示，三角形ABC有与之对应的矩形ABNM，且矩形面积是三角形的两倍，三角形ADC和CMA全等，CDB和BNC全等。

我们可以先生成矩形ABNM内的随机点P，如果P刚好在三角形ABC中，那么符合要求；如果P不在三角形ABC中，P要么在AMC中，要么在BNC中，如图P在BNC中，我们求P关于BC中点的的中心对称点，该点一定在三角形中。P在AMC中同理。这样可以保重三角形外的点都可以均匀的一一对应到三角形内部。

后面的代码中，为了简化计算，我们假设AB是平行X轴的。

对于生成任意多边形内的随机点，我们可以把它分割成三角形，再来生成随机点。

算法5和算法6的代码如下(Python3.3):

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as line
import random
import math

#对应博客算法5
def GeneratePointInTriangle1(point_num, pointA, pointB, pointC):
    for i in range(1, point_num+1):
        u = random.uniform(0.0, 1.0)
        v = random.uniform(0.0, 1.0 - u)
        pointP = u*pointC + v*pointB + (1.0-u-v)*pointA;
        plt.plot(pointP[0], pointP[1], '*', color = "black")

#根据向量叉乘计算三角形面积，参考 http://www.cnblogs.com/TenosDoIt/p/4024413.html
def ComputeTriangleArea(pointA, pointB, pointC):
    return math.fabs(np.cross(pointB - pointA, pointB - pointC)) / 2.0

#判断点P是否在三角形ABC内,参考 http://www.cnblogs.com/TenosDoIt/p/4024413.html
def IsPointInTriangle(pointA, pointB, pointC, pointP):
    area_abc = ComputeTriangleArea(pointA, pointB, pointC)
    area_pab = ComputeTriangleArea(pointA, pointB, pointP)
    area_pbc = ComputeTriangleArea(pointP, pointB, pointC)
    area_pac = ComputeTriangleArea(pointP, pointA, pointC)
    return math.fabs(area_pab + area_pac + area_pbc - area_abc) < 0.000001

#计算一个点关于某一点的中心对称点
def ComputeCentralSymmetryPoint(point_src, point_center):
    return np.array([point_center[0]*2-point_src[0], point_center[1]*2-point_src[1]])

#对应博客算法6
def GeneratePointInTriangle2(point_num, pointA, pointB, pointC):
    for i in range(1, point_num+1):
        pointP = np.array([random.uniform(pointA[0], pointB[0]), random.uniform(pointA[1], pointC[1])])
        if not IsPointInTriangle(pointA, pointB, pointC, pointP):
            if pointP[0] > pointC[0]:
                pointP = ComputeCentralSymmetryPoint(pointP, np.array([(pointC[0] + pointB[0])/2, (pointC[1] + pointB[1])/2]))
            else:
                pointP = ComputeCentralSymmetryPoint(pointP, np.array([(pointC[0] + pointA[0])/2, (pointC[1] + pointA[1])/2]))
        plt.plot(pointP[0], pointP[1], '*', color = "black")        


fig = plt.figure()
#三角形三个顶点
pointA = np.array([0,1])
pointB = np.array([3,1])
pointC = np.array([1,2])

plt.plot([pointA[0],pointB[0]], [pointA[1],pointB[1]])
plt.plot([pointA[0],pointC[0]], [pointA[1],pointC[1]])
plt.plot([pointB[0],pointC[0]], [pointB[1],pointC[1]])

GeneratePointInTriangle2(1500, pointA, pointB, pointC) #修改此处来显示不同算法的效果

plt.ylim(0.5,2)
plt.xlim(0,3)
plt.show()

【版权声明】转载请注明出处：http://www.cnblogs.com/TenosDoIt/p/4025221.html

转载于:https://www.cnblogs.com/TenosDoIt/p/4025221.html