数据结构——线性表

线性表

从数据的逻辑结构上来分 ，数据元素之间存在的关联关系被称为数据的逻辑结
构，应用程序中的数据大致分为如下4类基本的逻辑结构

• 集合：数据元素之间只有“同属于一个集合”的关系
• 线性结构：数据结构之间存在一对一的关系
• 树形结构：数据元素之间存在一对多的关系

• 图状结构或网状结构：数据元素之间存在多个对多个的关系

  对于不同的逻辑结构，计算机在磁盘上通常有2种物理机构
  

• 顺序存储结构

• 链式存储结构

线性表定义及其逻辑结构

线性表（Linear List）是由 n(n>=0)个元素组成的有限序列，线性表中每个元素
必须有相同的结构，线性表中包含的数据元素的个数n叫做表的长度，当线性表长度
为0时称为空表，对于一个非空的，有限的线性表来说，它有一下特征：

• 总存在唯一的”第一个”元素
• 总存在唯一的”最后一个”元素
• 除了第一个元素以外，列表中的每一个元素都有唯一的 前驱元素
• 除了最后一个元素外，列表中的每一个元素都有唯一的 后继元素

顺序存储结构的线性表

顺序存储是指用一组地址连续的存储单元依次存放线性表的元素，为了使用顺序结构
实现线性表，程序通常采用数组来保存元素,下面是线性表java简易实现

package day3;

import java.util.Arrays;

/**
 * Created by aura-bd on 2018/8/7.
 */
public class MyArrayList {
    //默认的列表大小
    private int DEFAULT_SIZE=16;
    //数组的长度
    private int capacity;
    //保存元素
    private Object[] element;
    //保存列表中当前元素的个数
    private int size;

    //默认构造器  --初始化数组长度
    public MyArrayList(){
        capacity=DEFAULT_SIZE;
        element=new Object[capacity];
    }
    //以指定长度来初始化列表
    public MyArrayList(int initSize){
        capacity=initSize;
        element=new Object[capacity];
    }

    //获取线性表的大小
    public int size(){
        return size;
    }

    //获取线性表中索引为i的元素
    public T get(int i){
        if (i<0 || i> size-1){
            throw new RuntimeException("越界");
        }else{
            return (T)element[i];
        }
    }
    //查找指定元素的索引
    public int get(T e){
        for (int i = 0; i if (element[i].equals(e)){
                return i;
            }
        }
        return -1;
    }

    //指定位置插入一个元素
    public void insert(int index,T e){
        if (index<0 || index> size){
            throw new RuntimeException("越界");
        }
        //确认是否需要扩容
        ensureCapacity(size+1);
        //将指定元素之后的所有元素向后移动一格
        System.arraycopy(element,index,element,index+1,size-index);
        element[index]=e;
        size++;
    }
    //添加一个元素
    public void add(T e){
        insert(size,e);
    }
    //删除线性表中指定索引处的元素
    public  T delete(int index){
        if (index<0 || index> size-1){
            throw new RuntimeException("越界");
        }
        //原来的值
        T oldValue=(T)element[index];
        //要移动的个数
        int numMoved=size-index-1;
        if (numMoved >0){
            System.arraycopy(element,index+1,element,index,numMoved);
        }
        element[--size]=null;
        return oldValue;
    }

    //删除线性表中最后一个元素
    public T remove(){
        return delete(size-1);
    }

    //判断线性表是否为空
    public boolean isEmpty(){
        return size==0;
    }

    //确认是否需要扩容
    private void ensureCapacity(int minCapacity){
        //如果数组的原有长度小于小于目前所需长度
        if(minCapacity > capacity){
            //不断地将capacity * 2 ,直到capacity大于 minCapacity
            while (minCapacity>capacity){
                capacity <<=1;
            }
            element= Arrays.copyOf(element,capacity);
        }
    }

    public String toString(){
        StringBuffer sb=new StringBuffer();
        for (int i = 0; i "\t");
        }
        return sb.toString();
    }
}

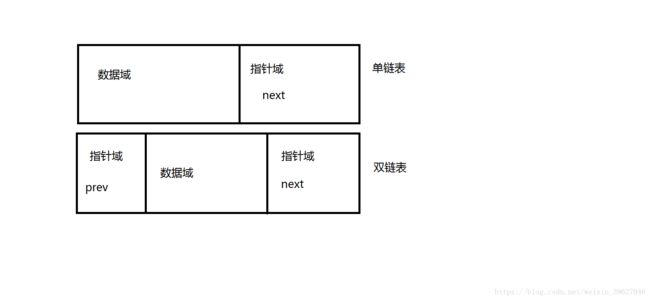
链式存储结构的线性表

   链式存储结构的线性表，也叫做链表，将采用一组地址任意的存储单元存放线性表中的数据元素，链
式结构的线性表不会按线性的逻辑顺序保存数据元素，它需要在每一个数据元素里保存一个下一个数据的
引用，因为不必按顺序存储，所以在插入元素，删除元素方面它比顺序线性表快的多，但是在查询方面它
比顺序线性表慢的多。
    使用链式结构可以克服顺序线性表（基于数组）需要预先知道数据大小的缺点，充分利用计算机内存
实现灵活的内存动态管理，但是链表结构失去了数组随机存储的优点，同时链表增加了指针域，空间开销
较大。以下为链表的示意图，next指向下一个元素的（后继），prev指向上一个元素（前驱），最后一
个元素的next引用为null,第一个元素的prev为null  

以下是单链表的简易实现，编程语言java：

package day3;

/**
 * Created by aura-bd on 2018/8/8.
 */
public class MyLinkedList {

    //定义一个内部类Node来保存元素，代表链表的节点
    private class Node{
        //保存节点的数据
        private T data;
        //指向下一个节点的引用
        private Node next;
        //无参构造器
        private Node(){}
        //带参构造器
        private Node(T data,Node next){
            this.next=next;
            this.data=data;
        }
    }

    //存储数据的头节点
    private Node header;
    //存储数据的尾节点
    private Node tail;
    //链表中的节点数
    private int size;
    //构造器初始化空链表
    public MyLinkedList(){
        this.header=null;
        this.tail=null;
    }
    //以指定元素创建链表
    public MyLinkedList(T e){
        //只有一个元素，所以它是头也是尾
        header=new Node(e,null);
        tail=header;
        size++;
    }

    //返回链表的长度
    public int length(){
        return size;
    }

    //获取线性表指定索引index的元素
    public T get(int index){
        return getNodeByIndex(index).data;
    }

    //根据索引index获取指定位置的节点
    private Node getNodeByIndex(int index){
        if (index<0 || index >size-1){
            throw new RuntimeException("索引越界");
        }
        //遍历节点，从头节点开始
        Node current=header;
        for (int i = 0; i < size && current!=null; i++,current=current.next) {
            if (i==index){
                return current;
            }
        }
        return null;
    }

    //根据指定元素查索引,查不到返回-1
    public int locate(T e){
        Node current=header;
        for (int i = 0; i null ; i++,current=current.next) {
            if (current.data.equals(e)){
                return i;
            }
        }
        return -1;
    }


    //往指定位置插入一个元素
    public void insert(int index,T e){
        if (index<0 || index >size-1){
            throw new RuntimeException("索引越界");
        }

        if (header==null){
            add(e);
        }else{
            //如果索引为0
            if (index==0){
                addHeader(e);
            }else{
                //获取插入点的前一个节点
                Node prev=getNodeByIndex(index-1);
                //让前一个节点指向当前节点，让当前节点指向下一个节点（前一个节点的下一个节点）
                prev.next=new Node(e,prev.next);
                size++;
            }

        }

    }
    //采用尾插法往列表里面添加数据
    public  void  add(T e){
        if (header==null){
            header=new Node(e,null);
            tail=header;
        }else{
            //创建一个新节点
            Node newNode=new Node(e,null);
            //让尾节点的指针指向新节点
            tail.next=newNode;
            //让新节点成为尾节点
            tail=newNode;
        }
        size++;
    }

    //采用头插法往列表里面添加数据
    public void addHeader(T e){
        if (header==null){
            header=new Node(e,null);
            tail=header;
        }else{
            //创建一个新节点
            Node newNode=new Node(e,null);
            //让尾节点的指针指向新节点
           newNode.next=header;
            //让新节点成为尾节点
            header=newNode;
        }
        size++;
    }

    //删除线性表中指定索引处的元素
    public T delete(int index){
        if (index < 0 || index >size-1){
            throw new RuntimeException("索引越界");
        }
        Node del=null;
        //如果要删除的是header节点
        if(index==0){
            del=header;
            header=header.next;
        }else {
            //获取要删除节点的前一个节点
            Node prev=getNodeByIndex(index-1);
            //要删除的节点
            del=prev.next;
            //让被删除的节点的上一个节点指向被删除节点的下一个节点
            prev.next=del.next;
            //将被删除的节点next置为null
            del.next=null;

        }

        T data=del.data;
        del=null;
        size--;
        return data;
    }

    //删除线性表最后一个元素
    public T remove(){
        return delete(size-1);
    }

    //判断是否为空表
    public boolean isEmpty(){
        return size==0;
    }
    //清空线性表
    public void clear(){
        header=null;
        tail=null;
        size=0;
    }
    //重写toString


    @Override
    public String toString() {
       if (size==0){
           return "[]";
       }
       StringBuilder sb=new StringBuilder("[");
        for (Node current=header; current!=null; current=current.next) {
            sb.append(current.data.toString()+", ");
        }
        int len=sb.length();
        return sb.delete(len-2,len).append("]").toString();
    }
}

    循环链表和双链表与单链表实现类似，双链表由于每一个数据元素不仅保存了下一个数据元素的引用
还保存了上一个数据元素的引用，所以在添加接待和删除节点上实现起来更复杂，而循环链表由于尾节点
的next指向了头节点，所以在循环链表中可以从任意一个节点找到表中的其他节点，所以循环链表被称为
无头无尾，方法实现上也更简单。