刷题---剪绳子（动态规划）

剪绳子

这道题与算法导论中的钢条切割问题很相似。除了最优化目标不同：钢条切割是在不同长度的钢条有不同的收益的基础上如何切割钢条使收益变得最大，这里减绳子是要剪成不同长度的绳子如何剪绳子使各个绳子长度的乘积最大。

我们先用暴力求解的递归方法思考：
cut-ro# 剪绳子
这道题与算法导论中的钢条切割问题很相似。除了最优化目标不同：钢条切割是在不同长度的钢条有不同的收益的基础上如何切割钢条使收益变得最大，这里减绳子是要剪成不同长度的绳子如何剪绳子使各个绳子长度的乘积最大。
我们先自己推算出n较小的情况，用来检验我们的程序正确性

n	p
2	1 =1*1
3	2=1*2
4	4=2*2
5	6=2*3
6	9=3*3
…	…

我们先用暴力求解的递归方法思考：
我们要求长度为$n$的绳子，求其剪下的各个长度之积最大是多少。我们可以分割问题，先剪下长度为$i$的一段，然后只剪剩下的长度为$n-i$的长度的绳子（递归求解）。于是递推式便为：
$$P\_cutRope(n)=\underset{1\le i<n}{\max }(i\ast P\_cutRope(n-i))n>1$$

于是代码是这样写的：

	public static int P_cutRope_recur(int n) {		
		//recur resolve
		int maxvalue = 0;
		if (n < 2)
            return 0;
        else if (n == 2)
            return 1;
            
		for(int i =1; i

但在求n=3时，返回的值maxvalue为1；
求n=4时，返回为3。
仔细一想，当n=3时，先切割长度为1的一段，剩下长度为2的绳子，单独针对长度为2的绳子做切割最优解为1，这就导致了n=3时的最优解本来是2段长度分别为1和2的绳子变成了长度为1的绳子*长度为2的绳子的最优解。
如果我们单纯的改变n=2的值为2，那如果这根绳子就是n=2，其实它的最优解为1。这就在递归的时候造成了一种矛盾。

因此这个递归函数本身如果不作修改是不可能改变这一现状，改变这一矛盾的方法就是立flag来区分我们到底是单纯的求n=2还是调用的n=2；

public static void main(String[] args) {
		int n = 10;
		for (int i=2;i<=n;i++) {
			System.out.print("n=" + i + "时， ");
			System.out.print(P_cutRope_recur_flag(i,0)+"\n");			
		}
	}	
	
public static int P_cutRope_recur_flag(int n,int flag) {		
		//recur resolve
		if (flag ==0) {		 //单纯的求n=2
			if(n==2) {
				return 1;
			}
		}
		int maxvalue = 0;
        if (n < 2) {
            return 0;
        }else if(n==2){
        	return 2;
        }
		for(int i =1; i

输出：

发现n=6时，对比上面的手推表，应该是9，然而这里是8。根据6=3+3；3*3=9来说，上面的代码没有考虑到n=3时有着跟n=2一样的情况，单独的求n=3，答案为2，但调用n=3时，最优的结果就为3。因此，上面没有考虑全面所有的单独求n跟递归调用n的情况。那么除了n=2和n=3，还有没有特例呢？
我们可以发现，从n=4开始，最优解就不有小于n的情况，也就是说，对于n大于等于4的递归调用，其递归结果一定大于n本身，因此就不需要再考虑到$P\_cutRope(n-i)<n-i$的情况。
$$P\_cutRope(n)=\underset{1\le i<n}{\max }(i\ast P\_cutRope(n-i))n>1$$

所以只需要加上n=3的情况。

public static int P_cutRope_recur_flag(int n,int flag) {		
		//recur resolve
		if (flag ==0) {  //单纯的求n=2和n=3
			if(n==2) {
				return 1;
			}else if(n==3){
				return 2;
			}
		}
		int maxvalue = 0;
        if (n < 2) {
            return 1;
        }else if(n==2){
        	return 2;
        }else if(n==3) {
        	return 3;
        }
		for(int i =1; i

输出为：

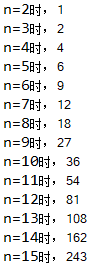
这个答案讲道理可以确保是正确的了。
接下来就是讨论递归的效率，我们以$n=6$举例并令$P(n)=P\_cutRope(n)$来简化表达：
$$P(7)=max(1\ast P(6),2\ast P(5),3\ast P(4),4\ast P(3),5\ast P(2),6\ast P(1))$$

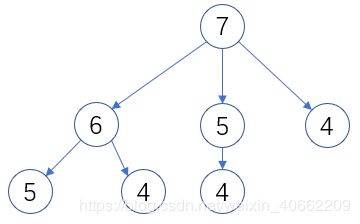
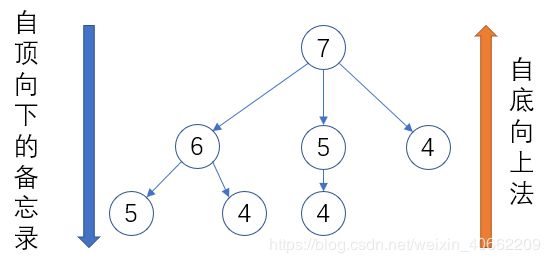
可以发现求P(7)是反复重复调用$P(4),P(5)$的，随着n的变大，这会极其消耗资源，工作量会像这棵树一样指数性的爆炸性的增长，并且每一次调用都有for循环浪费时间。
最容易想到的就是记录曾经求过的值，遇到则直接返回。这种方法被称为自顶向下的备忘录法。

自顶向下的备忘录法

	public static int P_cutRope_recur_flag_memo(int n,int flag,int[] r) {		
		//recur resolve
		if (flag ==0) { //单纯的求n=2
			if(n==2) {
				return 1;
			}else if(n==3){
				return 2;
			}
		}
		int maxvalue = 0;
	
		if(r[n]>=0) {
			return r[n];
		}
        if (n < 2) {
            return 1;
        }else if(n==2){
        	return 2;
        }else if(n==3) {
        	return 3;
        }
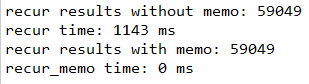
		for(int i =1; i

比较带备忘录的程序运行时间：

	public static void main(String[] args) {
		int n = 30;

			
		long starttime = System.currentTimeMillis();
		System.out.println("recur results without memo: "+P_cutRope_recur_flag(n,0));
		long endtime = System.currentTimeMillis();
		System.out.println("recur time: "+ (endtime - starttime)+" ms");
		
		long starttime1 = System.currentTimeMillis();
		int[] r = new int[n+1];
		for (int i =0;i<=n;i++) {
			r[i] = -1;
		}
		System.out.println("recur results with memo: "+P_cutRope_recur_flag_memo(n,0,r));
		long endtime1 = System.currentTimeMillis();
		System.out.println("recur_memo time: "+(endtime1 - starttime1)+" ms");
	}

结果显而易见：

自底向上法(bottomUp method)

自底向上与自顶向下的区别是：更大的解依赖于更小的解的答案，因此我们先求完更小的解答案。
每一个问题的求解依赖于更小的子问题的求解，因此先把更小的子问题求解保存，等到更大的子问题需要时，直接赋予它。
我们再次分析递归式：
$$P\_cutRope(n)=\underset{1\le i<n}{\max }(i\ast P\_cutRope(n-i))n>1$$

$$P(7)=max(1\ast P(6),2\ast P(5),3\ast P(4),4\ast P(3),5\ast P(2),6\ast P(1))$$

先求$P(4),P(5)$，$P(6)$就出来了，$P(7)$也因为$P(6)$的出现也出来了。

	public static int P_cutRope_recur_flag_bottomUp(int n) { //自底向上的动态规划
		int[] P = new int[n+1];
		for (int i =0;i<=n;i++) {
			P[i] = -1;
		}
		if(n<2) {
			P[1] = 1;
			return P[1];
		}else if(n==2) {
			P[2] = 1;
			return P[2];
		}else if(n==3) {
			P[3] =2;
			return P[3] ;
		}
		for(int i = 1; i<4; i++) {
			P[i] = Math.max(i, P[i]);
		}
		for(int i =4; i

当n=1000时，自底向上法比带备忘录的自顶向下法更快。简单的递归则等到猴年马月了。

总结：

首先这个问题仔细思考能得出它满足最优子结构性质，因此问题的最优解由相关子问题的最优解组合而成，而这些子问题可以独立求解，因此第一步是手动推出它的优化模型，这一步非常重要，不然一切代码都无从写起，然后暴力求解，一般使用递归。
同时，写出来的递归程序的效率很低的最重要原因是因为它反复递归了很多重复的子问题，动态规划保证每个子问题只求一次，然后保存下来供下次调用。动态规划的实质就是付出额外的内存空间来节省计算时间。

动态规划有两种等价的实现方法：

1. 自顶向下的备忘录法：
   top-down with memo 创建一个额外的内存空间（数组），因为我们的求解是自顶向下的，所以记录求过的相关子问题保存在数组上，在递归代码基础上很简单的修改就行了。
2. 自底向上法
   因为更大的问题总依赖于更小的子问题，bottom-up求出所有的子问题保存下来供更大的问题调用，因为求出了所有的子问题答案，所以它避免了递归的函数调用（因为递归就是自顶向下的搜索结构）。

两种算法的开销：
动态规划的总运行时间是多项式阶的。
自顶向下的备忘录法根据问题找答案，所以它并不一定会递归求解所有的可能的子问题，只求解与其相关的子问题。但因为其频繁的调用递归函数，其时间复杂性比自底向上法更大。两者相差的时间复杂度应该也只是一个系数的问题。并且实践证明，自底向上是更占优势的。

我觉得只要遇到满足 最优子结构+重叠子问题的问题就大胆的 用动态规划。