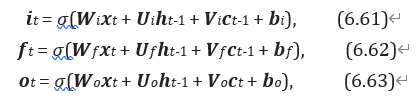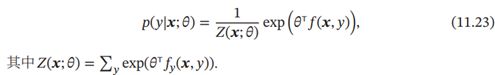自然语言处理入门练习（四）：基于LSTM+CRF的序列标注（附代码）

自然语言处理入门练习（四）：基于LSTM+CRF的序列标注（附代码）

一、基于门控的循环神经网络

  为了改善循环神经网络的长程依赖问题， 一种非常好的解决方案是在公式 = -1 + (, -1; )的基础上引入门控机制来控制信息的累积速度， 包括有选择地加入新的信息， 并有选择地遗忘之前累积的信息。这一类网络可以称为基于门控的循环神经网络（ Gated RNN）。本节中， 主要介绍两种基于门控的循环神经网络： 长短期记忆网络和门控循环单元网络。

1 长短期记忆网络

  长短期记忆网络（ Long Short-Term Memory Network， LSTM） [Gers et al., 2000; Hochreiter et al., 1997]是循环神经网络的一个变体， 可以有效地解决简单循环神经网络的梯度爆炸或消失问题。
  在公式 = -1 + (, -1; ), (6.50)的基础上， LSTM网络主要改进在以下两个方面：

• 新的内部状态 LSTM网络引入一个新的内部状态（ internal state） ∈ ℝ 专门进行线性的循环信息传递， 同时（ 非线性地） 输出信息给隐藏层的外部状态 ∈ ℝ． 内部状态 通过下面公式计算：
  
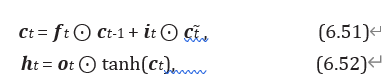
    其中 ∈ [0, 1]、 ∈ [0, 1] 和 ∈ [0, 1] 为三个门（ gate） 来控制信息传递的路径； ⊙为向量元素乘积； -1 为上一时刻的记忆单元； ̃ ∈ ℝ 是通过非线性函数得到的候选状态：

  在每个时刻， LSTM网络的内部状态 记录了到当前时刻为止的历史信息。

  - 门控机制 在数字电路中， 门（ gate） 为一个二值变量{0, 1}， 0代表关闭状态， 不许任何信息通过； 1代表开放状态， 允许所有信息通过。
  LSTM 网络引入门控机制（ Gating Mechanism） 来控制信息传递的路径。
  公式 (6.51) 和公式 (6.52) 中三个“门” 分别为输入门、 遗忘门 和输出门。 这三个门的作用为
  （ 1） 遗忘门 控制上一个时刻的内部状态-1 需要遗忘多少信息。
  （ 2） 输入门 控制当前时刻的候选状态̃ 有多少信息需要保存。
  （ 3） 输出门 控制当前时刻的内部状态 有多少信息需要输出给外部状态。

  当 = 0, = 1时， 记忆单元将历史信息清空， 并将候选状态向量̃ 写入．但此时记忆单元 依然和上一时刻的历史信息相关。 当 = 1, = 0 时， 记忆单元将复制上一时刻的内容， 不写入新的信息。

  LSTM网络中的“门” 是一种“软” 门， 取值在 (0, 1) 之间， 表示以一定的比例允许信息通过。 三个门的计算方式为：

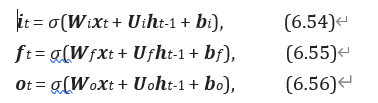
  其中 (⋅) 为 Logistic 函数， 其输出区间为 (0, 1)， 为当前时刻的输入， -1 为上一时刻的外部状态。

  图6.7给出了 LSTM 网络的循环单元结构， 其计算过程为： 1） 首先利用上一时刻的外部状态-1 和当前时刻的输入， 计算出三个门， 以及候选状态̃ ； 2）结合遗忘门 和输入门 来更新记忆单元 ； 3） 结合输出门 ， 将内部状态的信息传递给外部状态。

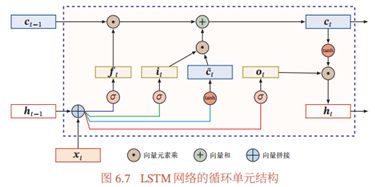
  通过 LSTM 循环单元， 整个网络可以建立较长距离的时序依赖关系。 公式(6.51)～公式(6.56)可以简洁地描述为

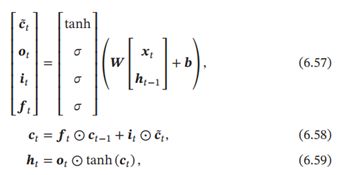
  其中 ∈ ℝ 为当前时刻的输入， ∈ ℝ4×(+) 和 ∈ ℝ4 为网络参数。

  记忆： 循环神经网络中的隐状态 存储了历史信息， 可以看作一种记（ Memory）。在简单循环网络中， 隐状态每个时刻都会被重写， 因此可以看作一种短期记忆（ Short-Term Memory）。 在神经网络中， 长期记忆（ Long-Term Memory） 可以看作网络参数， 隐含了从训练数据中学到的经验， 其更新周期要远远慢于短期记忆． 而在 LSTM 网络中， 记忆单元 可以在某个时刻捕捉到某个关键信息， 并有能力将此关键信息保存一定的时间间隔。记忆单元 中保存信息的生命周期要长于短期记忆 ， 但又远远短于长期记忆， 因此称为长短期记忆（ Long Short-Term Memory）。

  一般在深度网络参数学习时， 参数初始化的值一般都比较小。但是在训练 LSTM 网络时， 过小的值会使得遗忘门的值比较小。 这意味着前一时刻的信息大部分都丢失了， 这样网络很难捕捉到长距离的依赖信息；并且相邻时间间隔的梯度会非常小， 这会导致梯度弥散问题。 因此遗忘的参数初始值一般都设得比较大， 其偏置向量 设为1或2。

2 LSTM网络的各种变体

  目前主流的 LSTM 网络用三个门来动态地控制内部状态应该遗忘多少历史信息， 输入多少新信息， 以及输出多少信息。 我们可以对门控机制进行改进并获得LSTM网络的不同变体。
   无遗忘门的 LSTM 网络 [Hochreiter et al., 1997] 最早提出的 LSTM 网络是没有遗忘门的， 其内部状态的更新为

  如之前的分析，记忆单元 会不断增大。当输入序列的长度非常大时， 记忆单元的容量会饱和，从而大大降低LSTM模型的性能。

  peephole 连接 ：另外一种变体是三个门不但依赖于输入 和上一时刻的隐状态-1， 也依赖于上一个时刻的记忆单元-1。

其中， 和 为对角矩阵。

  耦合输入门和遗忘门： LSTM 网络中的输入门和遗忘门有些互补关系， 因此同时用两个门比较冗余。为了减少LSTM网络的计算复杂度， 将这两门合并为一个门。 令 = 1 - ， 内部状态的更新方式为

3 门控循环单元网络

  门控循环单元（ Gated Recurrent Unit， GRU） 网络 [Cho et al., 2014; Chung et al., 2014]是一种比LSTM网络更加简单的循环神经网络。
  GRU 网络引入门控机制来控制信息更新的方式。和 LSTM 不同， GRU 不引入额外的记忆单元， GRU网络也是在公式 = -1 + (, -1; )(6.50)的基础上引入一个更新门（ Update Gate） 来控制当前状态需要从历史状态中保留多少信息（ 不经过非线性变换）， 以及需要从候选状态中接受多少新信息。

其中 ∈ [0, 1] 为更新门，

  在LSTM网络中， 输入门和遗忘门是互补关系， 具有一定的冗余性。GRU网络直接使用一个门来控制输入和遗忘之间的平衡。 当 = 0 时， 当前状态 和前一时刻的状态-1 之间为非线性函数关系； 当 = 1时， 和-1 之间为线性函数关系。
  在GRU网络中， 函数(, -1; )的定义为

  其中̃ 表示当前时刻的候选状态， ∈ [0, 1] 为重置门（ Reset Gate）

  用来控制候选状态̃ 的计算是否依赖上一时刻的状态-1。

  当 = 0时， 候选状态̃ = tanh( + )只和当前输入 相关， 和历史状态无关。 当 = 1 时， 候选状态 ̃ = tanh(ℎ + ℎ-1 + ℎ) 和当前输入 以及历史状态-1 相关， 和简单循环网络一致。

  综上， GRU网络的状态更新方式为

  可以看出， 当 = 0, = 1时， GRU网络退化为简单循环网络； 若 = 0, = 0时， 当前状态 只和当前输入 相关， 和历史状态-1 无关． 当 = 1时， 当前状态 = -1 等于上一时刻状态-1， 和当前输入 无关。

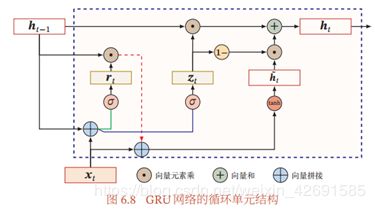
  图6.8给出了GRU网络的循环单元结构。

二、无向图模型

1 无向图模型

  无向图模型， 也称为马尔可夫随机场（ Markov Random Field， MRF） 或马尔可夫网络（ Markov Network）， 是一类用无向图来描述一组具有局部马尔可夫性质的随机向量 的联合概率分布的模型。

  定义 11.2 – 马尔可夫随机场： 对于一个随机向量 = [1, ⋯ , ]T 和一个有 个节点的无向图 (, ℰ)（ 可以存在循环）， 图 中的节点 表示随机变量， 1 ≤ ≤ ． 如果(, )满足局部马尔可夫性质， 即一个变量 在给定它的邻居的情况下独立于所有其他变量，

  其中 () 为变量 的邻居集合， K 为除 外其他变量的集合， 那么(, )就构成了一个马尔可夫随机场。

  无向图的局部马尔可夫性质： 无向图中的局部马尔可夫性质可以表示为

其中K(),K 表示除() 和 外的其他变量。
  对于图11.2b中的4个变量， 根据马尔可夫性质， 可以得到 1 ⟂ 4|2, 3 和 2 ⟂ 3|1, 4。

2 无向图模型的概率分解

  ==团 ==：由于无向图模型并不提供一个变量的拓扑顺序， 因此无法用链式法则对()进行逐一分解。无向图模型的联合概率一般以全连通子图为单位进行分解。无向图中的一个全连通子图， 称为团（ Clique）， 即团内的所有节点之间都连边。在图11.7所示的无向图中共有 7 个团， 包括 {1, 2}， {1, 3}， {2, 3}， {3, 4}，{2, 4}， {1, 2, 3}， {2, 3, 4}。

  在所有团中， 如果一个团不能被其他的团包含， 这个团就是一个最大团（ Maximal Clique）。

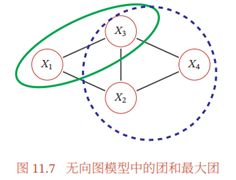
  因子分解：无向图中的联合概率可以分解为一系列定义在最大团上的非负函数的乘积形式。

  定理 11.1 – Hammersley-Clifford 定理： 如果一个分布 () 0 满足无向图 中的局部马尔可夫性质， 当且仅当()可以表示为一系列定义在最大团上的非负函数的乘积形式， 即

  其中 为 中的最大团集合， () ≥ 0 是定义在团 上的势能函数（ Potential Function）， 是配分函数（ Partition Function）， 用来将乘积归一化为概率形式：

  其中 为随机向量 的取值空间。

  Hammersley-Clifford 定理的证明可以参考 [Koller et al., 2009]． 无向图模型与有向图模型的一个重要区别是有配分函数。 配分函数的计算复杂度是指数级的， 因此在推断和参数学习时都需要重点考虑。
  吉布斯分布 公式 (11.16) 中定义的分布形式也称为吉布斯分布（ Gibbs Distribution）。 根据 Hammersley-Clifford 定理， 无向图模型和吉布斯分布是一致的．吉布斯分布一定满足马尔可夫随机场的条件独立性质， 并且马尔可夫随机场的概率分布一定可以表示成吉布斯分布。

  由于势能函数必须为正， 因此我们一般定义为

  其中()为能量函数（ Energy Function）。

  因此， 无向图上定义的概率分布可以表示为

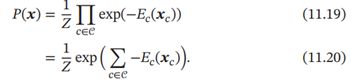
  这种形式的分布又称为玻尔兹曼分布（ Boltzmann Distribution）。任何一个无向图模型都可以用公式(11.20)来表示其联合概率。

3 常见的无向图模型

  很多经典的机器学习模型可以使用无向图模型来描述， 比如对数线性模型（ 也叫最大熵模型）、条件随机场、玻尔兹曼机、受限玻尔兹曼机等。

3.1 对数线性模型

  势能函数一般定义为

  其中函数 () 为定义在 上的特征向量， 为权重向量． 这样联合概率 ()的对数形式为

  其中 代表所有势能函数中的参数 ． 这种形式的无向图模型也称为对数线性模型（ Log-Linear Model） 或最大熵模型（ Maximum Entropy Model） [Bergeret al., 1996; Della Pietra et al., 1997]． 图11.8a所示是一个常用的最大熵模型。
  如果用对数线性模型来建模条件概率(|)，

  对数线性模型也称为条件最大熵模型或Softmax回归模型。

3.2 条件随机场

  条件随机场（ Conditional Random Field， CRF） [Lafferty et al., 2001]是一种直接建模条件概率的无向图模型。
  和条件最大熵模型不同， 条件随机场建模的条件概率(|)中， 一般为随机向量， 因此需要对 (|) 进行因子分解。 假设条件随机场的最大团集合为 ，其条件概率为

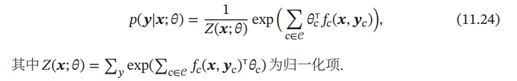
  一个最常用的条件随机场为图11.8b中所示的链式结构， 称为线性链条件随机场（ Linear-Chain CRF）， 其条件概率为

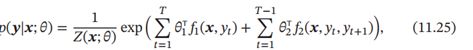
  其中 1(, ) 为状态特征， 一般和位置 相关， 2(, , +1) 为转移特征， 一般可以简化为2(, +1)并使用状态转移矩阵来表示。

三、同步的序列到序列模式

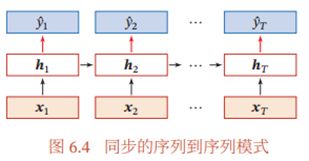
  同步的序列到序列模式主要用于序列标注（ Sequence Labeling） 任务， 即每一时刻都有输入和输出， 输入序列和输出序列的长度相同． 比如在词性标注（ Part-of-Speech Tagging） 中， 每一个单词都需要标注其对应的词性标签。

  在同步的序列到序列模式（ 如图6.4所示） 中， 输入为一个长度为 的序列1∶ = (1, ⋯ , )， 输出为序列 1∶ = (1, ⋯ , )． 样本 按不同时刻输入到循环神经网络中， 并得到不同时刻的隐状态 1, ⋯ , 。 每个时刻的隐状态 代表了当前时刻和历史的信息， 并输入给分类器(⋅)得到当前时刻的标签̂ ， 即

四、BiLSTM+CRF

  BiLSTM也可以做序列标注的问题，只需要在每一步的隐藏层的输出接上一个[n_hidden, n_label]的映射矩阵，然后用softmax做一个多分类。

  BiLSTM可以捕捉长距离的上下文信息，对于每一步能获得很好的语意向量，CRF是对整个序列进行似然概率统计，并且捕捉转换信息，将两者结合起来可以互补不足。

  CRF能为BiLSTM提供转换的一些约束，拿词性标注举例子，形容词后面大概率会跟名词，名词后面大概率会跟动词，还可以提供整个序列的概率统计，前面出现了某些单词后，这个位置应该是谓词。因为LSTM只是对每一步的向量进行过滤和叠加，这些信息是LSTM不好捕捉的。

  根据论文：《End-to-end Sequence Labeling via Bi-directional LSTM-CNNs-CRF》

  用字符级别的embedding作为输入捕捉字符信息，然后将其跟单词embedding concat起来作为Bi-LSTM的输入。然后Bi-LSTM的输出给到CRF模型来进行序列的联合解码。Bi-LSTM的输入和输出都加了dropout。实验表明dropout可以有效提升模型表现。

【实战任务】

  用LSTM+CRF来训练序列标注模型：以Named Entity Recognition为例。

【核心代码】

main.py

import pickle
import pdb
import numpy as np 
from sklearn.metrics import precision_score, recall_score, f1_score, classification_report
from config import opt 
import torch
from torch.utils.data import Dataset,DataLoader
import torch.nn as nn
import torch.optim as optim
from model.LSTM import NERLSTM
from model.LSTM_CRF import NERLSTM_CRF
from utils import get_tags, format_result


with open(opt.pickle_path, 'rb') as inp:
        word2id = pickle.load(inp)
        # id2word = pickle.load(inp)
        tag2id = pickle.load(inp)
        # id2tag = pickle.load(inp)
        x_train = pickle.load(inp)
        y_train = pickle.load(inp)
        x_test = pickle.load(inp)
        y_test = pickle.load(inp)
        x_valid = pickle.load(inp)
        y_valid = pickle.load(inp)
print("train len:", len(x_train))
print("test len:", len(x_test))
print("valid len", len(x_valid))
print(word2id)
print(tag2id)


class NERDataset(Dataset):
    def __init__(self, X, Y, *args, **kwargs):
        self.data = [{'x': X[i], 'y':Y[i]} for i in range(X.shape[0])]

    def __getitem__(self, index):
        return self.data[index]

    def __len__(self):
        return len(self.data)

train_dataset = NERDataset(x_train, y_train)
valid_dataset = NERDataset(x_valid, y_valid)
test_dataset = NERDataset(x_test, y_test)

train_dataloader = DataLoader(train_dataset, batch_size=opt.batch_size, shuffle=True, num_workers=opt.num_workers)
valid_dataloader = DataLoader(valid_dataset, batch_size=opt.batch_size, shuffle=True, num_workers=opt.num_workers)
test_dataloader = DataLoader(test_dataset, batch_size=opt.batch_size, shuffle=True, num_workers=opt.num_workers)


models = {'NERLSTM': NERLSTM,
          'NERLSTM_CRF': NERLSTM_CRF}

model = models[opt.model](opt.embedding_dim, opt.hidden_dim, opt.dropout, word2id, tag2id)
criterion = nn.CrossEntropyLoss(ignore_index=0)
optimizer = optim.Adam(model.parameters(), lr=opt.lr, weight_decay=opt.weight_decay)

class ChineseNER(object):
    def train(self):
        for epoch in range(opt.max_epoch):
            model.train()
            for index, batch in enumerate(train_dataloader):
                optimizer.zero_grad()
                X = batch['x']
                y = batch['y']
                # CRF
                loss = model.log_likelihood(X, y)
                loss.backward()
                # CRF
                torch.nn.utils.clip_grad_norm_(parameters=model.parameters(), max_norm=10)

                optimizer.step()
                if index % 200 == 0:
                    print('epoch:%04d,------------loss:%f'%(epoch,loss.item()))

            aver_loss = 0
            preds, labels = [], []
            for index, batch in enumerate(valid_dataloader):
                model.eval()
                val_x, val_y = batch['x'], batch['y']
                predict = model(val_x)
                # CRF
                loss = model.log_likelihood(val_x, val_y)
                aver_loss += loss.item()
                # 统计非0的，也就是真实标签的长度
                leng = []
                for i in val_y.cpu():
                    tmp = []
                    for j in i:
                        if j.item() > 0:
                            tmp.append(j.item())
                    leng.append(tmp)

                for index, i in enumerate(predict):
                    preds += i[:len(leng[index])]

                for index, i in enumerate(val_y.tolist()):
                    labels += i[:len(leng[index])]
            aver_loss /= (len(valid_dataloader) * 64)
            precision = precision_score(labels, preds, average='macro')
            recall = recall_score(labels, preds, average='macro')
            f1 = f1_score(labels, preds, average='macro')
            report = classification_report(labels, preds)
            print(report)
            torch.save(model.state_dict(), './model/params.pkl')

    def predict(self, tag, input_str=""):
        model.load_state_dict(torch.load("./model/params.pkl"))
        if not input_str:
            input_str = input("请输入文本: ")
        input_vec = [word2id.get(i, 0) for i in input_str]
        # convert to tensor
        sentences = torch.tensor(input_vec).view(1, -1)
        paths = model(sentences)

        entities = []
        tags = get_tags(paths[0], tag, tag2id)
        entities += format_result(tags, input_str, tag)
        print(entities)

if __name__ == '__main__':
    cn = ChineseNER()
    cn.train = []
    # cn.predict('ns')

结果：

【完整代码github地址】

https://github.com/chenlian-zhou/nlp/tree/master/nlp_induction_training/task4

【参考资料】

1. 邱锡鹏的《神经网络与深度学习》
2. 论文推荐：
   End-to-end Sequence I abeling via Bi-directional LSTM-CNNs-CRF
   Neural Architectures for Named Entity Recognition
3. https://github.com/FudanNLP/nlp-beginner