深度学习笔记（14）：第二课第一周第二次作业

剖析与心得

这一部分也比较简单啦。主要是练习实践一下正则化的两个手段：L₂正则化和$dropout$方法。
先码一下知识点：
1，L₂正则化是在代价函数的尾部追加所有权重矩阵的F范数再乘以 $\frac{\lambda }{2m}$.在反向传播的时候求导结果是在$dw$^[i]后面追加了一个$\frac{\lambda }{m}\ast w$^[i]（也就是:$dz$^[i]$\ast a$^[i-1]T+$\frac{\lambda }{m}\ast w$^[i]，值得注意的是我们求导之后的结果应该是对应回去的，正则项求导出来的是一个矩阵而不是一个数）。也就是说实际上在最后梯度下降的时候，我们的公式从$w$^[i]=$w$^[i]-$dz$^[i]$\ast a$^[i-1]T变成了$w$^[i]=$w$^[i]-$\alpha \ast$($dz$^[i]$\ast a$^[i-1]T-$\frac{\lambda }{m}\ast w$^[i])，展开可以改写成$w$^[i]=(1-$\frac{\alpha \lambda }{m})\ast w$^[i]-$\alpha \ast$$dz$^[i]$\ast a$^[i-1]T我们观察发现，区别仅仅在于每次除了减以外，还要在$w$乘上一个权重系数。所以我们加了正则项之后的下降也被称作权重梯度下降。$\lambda$越大，权重越大，那么模型就越简单，反之就越复杂。

2，$dropout$正则化，吴恩达在作业中用了一个很有趣的比喻：
““
要了解Dropout，可以思考与朋友进行以下对话：

• 朋友：“为什么你需要所有神经元来训练你的网络以分类图像？”。
• 你：“因为每个神经元都有权重，并且可以学习图像的特定特征/细节/形状。我拥有的神经元越多，模型学习的特征就越丰富！”
• 朋友：“我知道了，但是你确定你的神经元学习的是不同的特征而不是全部相同的特征吗？”
• 你：“这是个好问题……同一层中的神经元实际上并不关联。应该绝对有可能让他们学习相同的图像特征/形状/形式/细节…这是多余的。为此应该有一个解决方案。”
  ””
  这就是原因之一，即实际上，我们使用$dropout$有一个原因就是拜托神经元之间的依赖性，使得其尽可能地学到更加丰富的特征。
  另一方面，我们相当于每一次只抽离出一部分的神经元来构建了更简单的神经网络模型，这样做降低神经元之间的耦合度，实际上就是在提高其广泛性与适用性。
  使用时，编程上我们要注意一些细节，$keep\_prob$是选择有多大比例的神经元被留下来，所以我们要将大于这个数的随机数掩码变换赋值为0，小于这个数的掩码变换赋值为1。然后我们要生成均匀的随机数，必须要使用np.random.rand，而不是np.random.randn。

代码部分

代码不难，细节前面基本也说过。大家有需要看看就好。
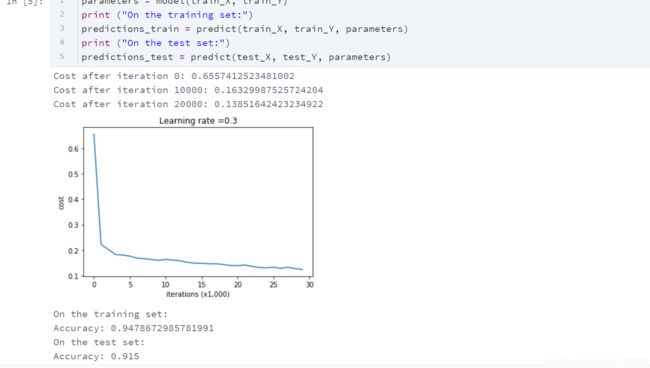
未正则化以前：过拟合现象严重。

L2正则化代码如下

# GRADED FUNCTION: compute_cost_with_regularization

def compute_cost_with_regularization(A3, Y, parameters, lambd):
    """
    Implement the cost function with L2 regularization. See formula (2) above.
    
    Arguments:
    A3 -- post-activation, output of forward propagation, of shape (output size, number of examples)
    Y -- "true" labels vector, of shape (output size, number of examples)
    parameters -- python dictionary containing parameters of the model
    
    Returns:
    cost - value of the regularized loss function (formula (2))
    """
    m = Y.shape[1]
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    W3 = parameters["W3"]
    
    cross_entropy_cost = compute_cost(A3, Y) # This gives you the cross-entropy part of the cost
    
    ### START CODE HERE ### (approx. 1 line)
    L2_regularization_cost = 1/2*lambd*1/m*(np.sum(np.square(W1))+np.sum(np.square(W2))+np.sum(np.square(W3))
)    ### END CODER HERE ###
    
    cost = cross_entropy_cost + L2_regularization_cost
    
    return cost

# GRADED FUNCTION: backward_propagation_with_regularization

def backward_propagation_with_regularization(X, Y, cache, lambd):
    """
    Implements the backward propagation of our baseline model to which we added an L2 regularization.

    Arguments:
    X -- input dataset, of shape (input size, number of examples)
    Y -- "true" labels vector, of shape (output size, number of examples)
    cache -- cache output from forward_propagation()
    lambd -- regularization hyperparameter, scalar

    Returns:
    gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
    """

    m = X.shape[1]
    (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache

    dZ3 = A3 - Y

    ### START CODE HERE ### (approx. 1 line)
    dW3 = 1/m*np.dot(dZ3,A2.T)+lambd/m*W3
    ### END CODE HERE ###
    db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)

    dA2 = np.dot(W3.T, dZ3)
    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    ### START CODE HERE ### (approx. 1 line)
    dW2 = 1/m*np.dot(dZ2,A1.T)+lambd/m*W2
    ### END CODE HERE ###
    db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)

    dA1 = np.dot(W2.T, dZ2)
    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    ### START CODE HERE ### (approx. 1 line)
    dW1 = 1/m*np.dot(dZ1,X.T)+lambd/m*W1
    ### END CODE HERE ###
    db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)

    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
                 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, 
                 "dZ1": dZ1, "dW1": dW1, "db1": db1}

    return gradients

L2正则化以后效果良好，过拟合现象减弱很多。
观察：

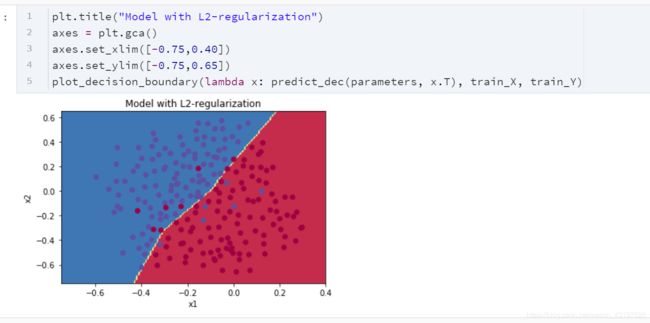
• $\lambda$ 的值是你可以调整开发集的超参数。
• L2正则化使决策边界更平滑。如果$\lambda$ 太大，则也可能“过度平滑”，从而使模型偏差较高。

L2正则化的原理：

L2正则化基于以下假设：权重较小的模型比权重较大的模型更简单。因此，通过对损失函数中权重的平方值进行惩罚，可以将所有权重驱动为较小的值。比重太大会使损失过高！这将导致模型更平滑，输出随着输入的变化而变化得更慢。

你应该记住 L2正则化的影响：

• 损失计算：
  • 正则化条件会添加到损失函数中
• 反向传播函数：
  • 有关权重矩阵的渐变中还有其他术语
• 权重最终变小（“权重衰减”）：
  • 权重被推到较小的值。

dropout代码如下（（前向\反向）传递，掩盖，传递，掩盖…）：

# GRADED FUNCTION: forward_propagation_with_dropout

def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
    """
    Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.
    
    Arguments:
    X -- input dataset, of shape (2, number of examples)
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
                    W1 -- weight matrix of shape (20, 2)
                    b1 -- bias vector of shape (20, 1)
                    W2 -- weight matrix of shape (3, 20)
                    b2 -- bias vector of shape (3, 1)
                    W3 -- weight matrix of shape (1, 3)
                    b3 -- bias vector of shape (1, 1)
    keep_prob - probability of keeping a neuron active during drop-out, scalar
    
    Returns:
    A3 -- last activation value, output of the forward propagation, of shape (1,1)
    cache -- tuple, information stored for computing the backward propagation
    """
    
    np.random.seed(0)
    
    # retrieve parameters
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]
    
    # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
    Z1 = np.dot(W1, X) + b1
    A1 = relu(Z1)
    ### START CODE HERE ### (approx. 4 lines)         # Steps 1-4 below correspond to the Steps 1-4 described above. 
    D1 = np.random.rand(A1.shape[0],A1.shape[1])             # Step 1: initialize matrix D1 = np.random.rand(..., ...)
    D1 = (D1>keep_prob)                          # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
    A1 = A1*D1                                   # Step 3: shut down some neurons of A1
    A1/=keep_prob                                # Step 4: scale the value of neurons that haven't been shut down
    ### END CODE HERE ###
    Z2 = np.dot(W2, A1) + b2
    A2 = relu(Z2)
    ### START CODE HERE ### (approx. 4 lines)
    D2 = np.random.rand(A2.shape[0],A2.shape[1])         # Step 1: initialize matrix D2 = np.random.rand(..., ...)
    D2 = (D2>keep_prob)                       # Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold)
    A2 = A2*D2                                 # Step 3: shut down some neurons of A2
    A2 /=keep_prob                        # Step 4: scale the value of neurons that haven't been shut down
    ### END CODE HERE ###
    Z3 = np.dot(W3, A2) + b3
    A3 = sigmoid(Z3)

    cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)

    return A3, cache

# GRADED FUNCTION: backward_propagation_with_dropout

def backward_propagation_with_dropout(X, Y, cache, keep_prob):
    """
    Implements the backward propagation of our baseline model to which we added dropout.
    
    Arguments:

    X -- input dataset, of shape (2, number of examples)
    Y -- "true" labels vector, of shape (output size, number of examples)
    cache -- cache output from forward_propagation_with_dropout()
    keep_prob - probability of keeping a neuron active during drop-out, scalar
    
    Returns:
    gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
    """
    
    m = X.shape[1]
    (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
    
    dZ3 = A3 - Y
    dW3 = 1./m * np.dot(dZ3, A2.T)
    db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
    dA2 = np.dot(W3.T, dZ3)
    ### START CODE HERE ### (≈ 2 lines of code)
    dA2 *= D2           # Step 1: Apply mask D2 to shut down the same neurons as during the forward propagation
    dA2 /= keep_prob  # Step 2: Scale the value of neurons that haven't been shut down
    ### END CODE HERE ###
    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    dW2 = 1./m * np.dot(dZ2, A1.T)
    db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)

    dA1 = np.dot(W2.T, dZ2)
    ### START CODE HERE ### (≈ 2 lines of code)
    dA1 *=D1           # Step 1: Apply mask D1 to shut down the same neurons as during the forward propagation
    dA1 /= keep_prob            # Step 2: Scale the value of neurons that haven't been shut down
    ### END CODE HERE ###
    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    dW1 = 1./m * np.dot(dZ1, X.T)
    db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)

    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
                 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, 
                 "dZ1": dZ1, "dW1": dW1, "db1": db1}
    
    return gradients

dropout之后的效果相当好，法国足球队很感谢！

后记和杂项

注意：

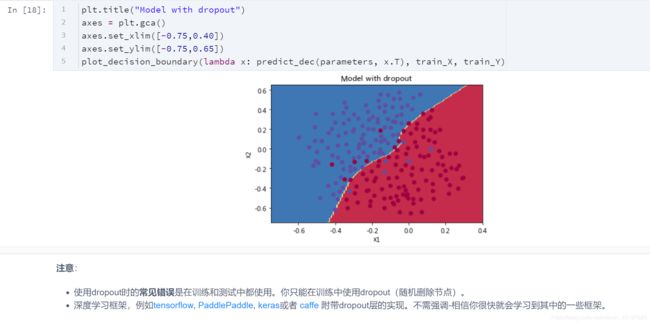
• 使用dropout时的常见错误是在训练和测试中都使用。你只能在训练中使用dropout（随机删除节点）。
• 深度学习框架，例如tensorflow, PaddlePaddle, keras或者 caffe 附带dropout层的实现。不需强调-相信你很快就会学习到其中的一些框架。

关dropout你应该记住的事情：

• dropout是一种正则化技术。
• 仅在训练期间使用dropout，在测试期间不要使用。
• 在正向和反向传播期间均应用dropout。
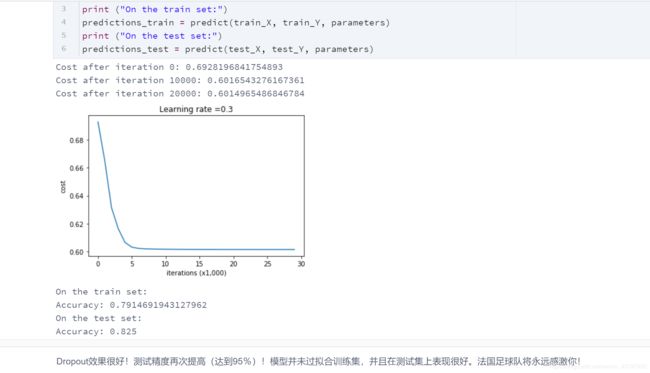
• 在训练期间，将每个dropout层除以keep_prob，以保持激活的期望值相同。例如，如果keep_prob为0.5，则平均而言，我们将关闭一半的节点，因此输出将按0.5缩放，因为只有剩余的一半对解决方案有所贡献。除以0.5等于乘以2，因此输出现在具有相同的期望值。你可以检查此方法是否有效，即使keep_prob的值不是0.5。（我做了一下实验，发现不除以权重的话下降的确很缓慢，即使迭代多次也效果一般）
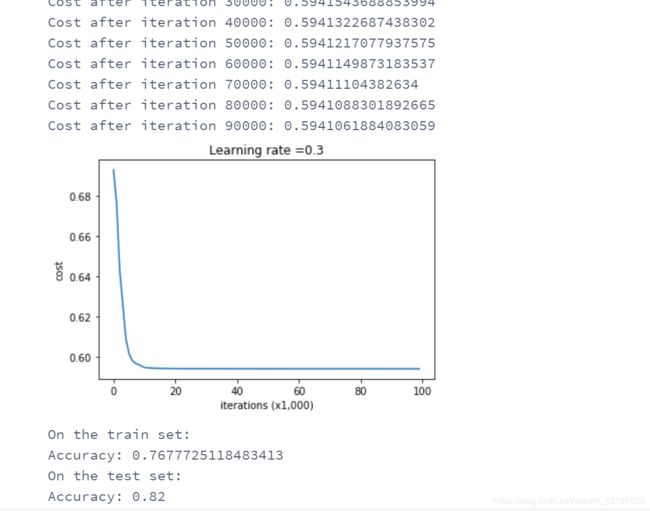  这是我们三个模型的结果：

模型	训练精度	测试精度
三层神经网络，无正则化	95％	91.50％
具有L2正则化的3层NN	94％	93％
具有dropout的3层NN	93％	95％

我们希望你从此笔记本中记住的内容：

• 正则化将帮助减少过拟合。
• 正则化将使权重降低到较低的值。
• L2正则化和Dropout是两种非常有效的正则化技术。