基于 python 的主成分分析步骤及应用实例
主成分分析:步骤、应用及代码实现。
主成分分析(Principal Component Analysis)算法步骤:
设有 m 条 n 维数据:
- 将原始数据按列组成 n 行 m 列矩阵 X
- 将 X 的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
- 求出协方差矩阵 C = 1 m X X T C=\frac{1}{m}XX^{T} C=m1XXT
- 求出协方差矩阵的特征值及对应的特征向量
- 将特征向量按对应特征值大小从上到下按行排列成矩阵,取前 k 行组成矩阵 P
- Y=PX 即为降维到 k 维后的数据
具体原理及步骤可以参考《机器学习实战》之十三——利用PCA来简化数据
这篇介绍十分详尽,是唯一一份我每一步推导都能看懂的对于 PCA 原理的讲解)
实际上,我们可以直接利用 sklearn 的 decomposition 模块进行主成分分析,只需要调整参数即可实现,例如:
sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)
但是,sklearn 中 PCA 算法,并不是对协方差矩阵进行特征分解,因为当样本数和样本特征数都较多的时候,计算协方差矩阵的计算量会很大。所以,sklearn 中的 PCA 采用的是 SVD(奇异值分解),在不求解协方差矩阵的情况下,得到右奇异矩阵 V。也就是说 PCA 算法可以不用做特征分解,而是做 SVD 来完成,这个方法在样本量很大的时候很有效。
应用实例:PCA example with Iris Data-set
关于数据集:
The iris dataset is a classic and very easy multi-class classification dataset.
The dataset contains a set of 150 records under five attributes - petal length, petal width, sepal length, sepal width and species.
以下是部分数据截图:
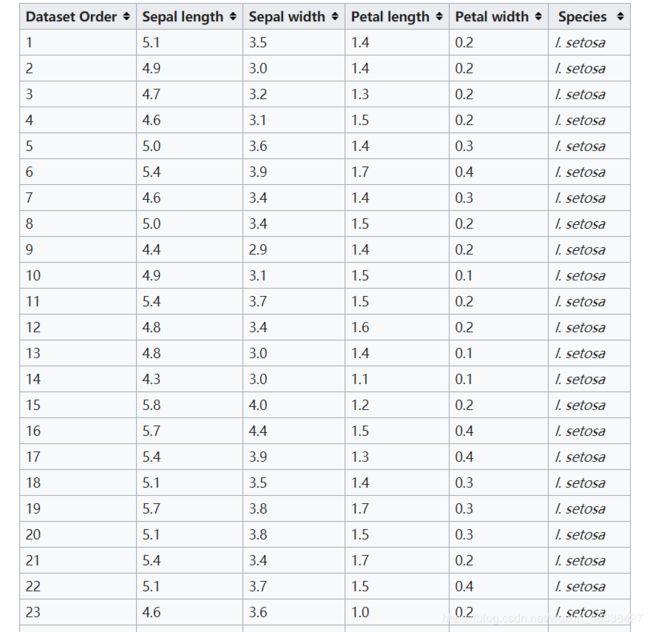
Language: python
IDE:jupyter notebook
具体代码如下:
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import decomposition
from sklearn import datasets
np.random.seed(5)
centers = [[1, 1], [-1, -1], [1, -1]]
iris = datasets.load_iris()
X = iris.data
y = iris.target
fig = plt.figure(1, figsize=(4, 3))
plt.clf()
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
plt.cla()
pca = decomposition.PCA(n_components=3)
pca.fit(X)
X = pca.transform(X)
for name, label in [('Setosa', 0), ('Versicolour', 1), ('Virginica', 2)]:
ax.text3D(X[y == label, 0].mean(),
X[y == label, 1].mean() + 1.5,
X[y == label, 2].mean(), name,
horizontalalignment='center',
bbox=dict(alpha=.5, edgecolor='w', facecolor='w'))
# Reorder the labels to have colors matching the cluster results
y = np.choose(y, [1, 2, 0]).astype(np.float)
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, cmap=plt.cm.nipy_spectral,
edgecolor='k')
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
plt.show()
运行结果如图:

最后,PCA 主要用于数据压缩或者数据降维减少内存或者硬盘的使用,能够加快机器学习的速度,也可以降维到2D或者3D从而实现数据可视化。
它的应用场景十分广泛,包括但不限于人脸识别、二级市场选股等等。这里只是利用最经典的应用实例进行分析,关于 PCA 的使用还有待进一步探索。