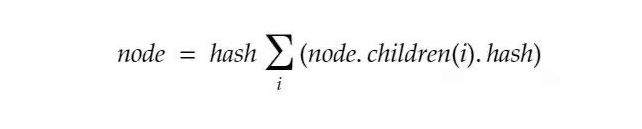区块链研究实验室｜实现Merkle-Tree和Patricia-Trie教程详解

本文介绍了Node.js中Merkle Tree和Patricia Trie的实现，还介绍了这两种数据结构的一些理论方面。

介   绍

Merkle和Patricia是以太坊区块链中使用的两种最受欢迎的数据结构，其背后的Bloom Filters非常接近。在本文中，我将介绍以下内容：

1. 关于Merkle和Patricia尝试

2. 算法

3. 在Node.js中实现

默克尔树Merkle Tree

默克尔树Merkle Tree不是计算机科学中的新概念，它已经存在了数十年，起源于密码学领域。

简而言之，默克尔树Merkle Tree本质上是一种树数据结构，其中数据存储在叶节点中，非叶节点存储数据散列，每个非叶节点是其下两个节点的组合哈希值。

从数学上讲，它可以表示为

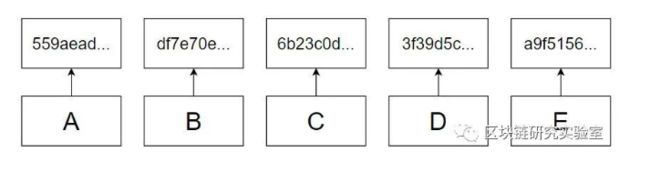
例如：给定一个字母表列表，从中创建一个默克尔树merkel tree。默克尔树merkel tree的最底层将包含所有字母作为叶节点。

上面的层包含其哈希值。

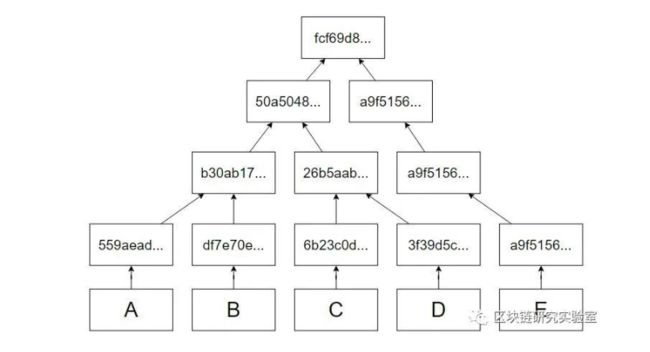
第二层之后的层中的节点包含子节点的哈希值。通常我们从第二层获取两个节点，并将它们合并以形成另一个节点。我们也可以采用两个以上的节点，但是二叉默克尔树merkel tree是所有节点中最简单的，增加节点的程度只会增加计算和算法的复杂性。

如果节点数为偶数，则取两个连续的节点并形成父层。但是如果节点数为奇数，我们将使用两个连续的节点，直到剩下一个以形成父层为止，然后通过将哈希值复制到父层来重复剩余的节点。

第3层具有第2层的2个连续节点的值的哈希值，如果我们在一层中有奇数个节点，则最后一个节点将被重复

类似地，使用第三层的值形成第四层。

第四层由第2层的2个连续节点的值的散列形成

默克尔树merkel tree的最后一层或根由保留在最顶层的最后两个节点的哈希值组成。在任何情况下，奇数或偶数叶节点，我们始终在最顶层具有两个节点。

数据验证

默克尔树merkel tree的重要性在于其高效验证数据的能力。在给定列表中的任何数据，我们可以在O（h）时间复杂度中验证此数据是否有效。而且我们不需要整个列表进行验证。

默克尔树merkel tree的一种更简单形式表现是哈希链或只是一个区块链，其中每个节点都具有前一个节点值的哈希值。如果我们篡改中间的任何节点，则可以在O（n）时间内确定该节点是否被篡改。哈希链中的验证可以通过计算所有节点的哈希值（从所讨论的节点开始直至结束）来执行。在需要验证多个节点的情况下，我们从所有可疑节点中的第一个节点开始，然后计算最后一个节点的哈希。现在我们有了最后一个节点的哈希，可以比较并检查此哈希是否匹配。哈希链看起来很简单，但对于大型数据对象而言并不是一个有效的选择。由于我们需要物理上存在的整个链来验证数据，因此这也会使哈希链空间效率低下。

默克尔树merkel tree的验证情况并非如此。为了说明验证过程，请考虑下面的示例。

假设我从另一台服务器收到了数据C。可以说这是C’。我们要验证C’是否未被篡改。我们没有列表中所有数据的默克尔树merkel tree。

如果是哈希链，我们将需要整个数据列表来验证C’是正确的。在默克尔树merkel tree中，我们只需要哈希即可。下图说明了如何在没有其他可用数据对象的情况下验证C'。

过对将我们引向根的所有节点进行散列来验证C’

1. 在列表中找到C’的位置。可通过ID搜索。

2. 计算C’的哈希值

3. 通过将当前节点与其邻居进行哈希运算来计算父节点的值（如果位置为奇数，则为下一个；如果位置为偶数，则为上一个），然后将父节点设置为当前节点。

4. 重复步骤3，直到找到根

5. 比较当前根和先前的根（如果它们匹配，则C'）

将新的根与现有的根进行比较。如果新的根匹配，则C’本质上是C，就没被篡改。

为了验证哈希链中的数据，我们需要O（n）时间，因为在最坏的情况下我们将计算n个哈希，就像在默克尔树的情况下一样，由于我们仅计算logn哈希，因此可以在O（logn）时间内验证相同的数据。

默克尔树merkel tree算法

本节以数学形式描述了用于在默克尔树merkel tree中创建和验证的算法。

创建

如前所述，默克尔树merkel tree是通过从每一层获取两个节点并对其进行哈希处理以创建父节点来创建的。通过以矩阵形式表示树，我们可以在数学上将其写为：

 

这使得树的根在tree [0] [0]可用

数据验证

数据验证是一种自下而上的方法，其中我们从数据开始，找到其哈希值并计算父级，然后继续进行直到找到根。在数学上，我们可以表示为：

 Patricia Tries

Patricia Tries是n元树，与默克尔树不同，它用于存储数据而不是进行验证。

简而言之，Patricia Tries是一种树型数据结构，其中所有数据都存储在叶节点中，其中每个非叶节点都是标识数据的唯一字符串的字符。使用唯一的字符串，我们浏览字符节点并最终到达数据。

Patricia Trie就像一个哈希表，但有一些细微的差异。

让我们看一个例子。请考虑以下单词：

Cat, Cats, Car, Dog, Dogs, Doggo, Ant

patricia trie存放这些物品看起来像这样：

值为END的节点表示到现在为止遍历的路径实际上是一个单词。那些没有END子节点的节点表示该单词不存在。

例如在上图中，由于END节点位于“ T”之后，所以单词ANT出现在trie中。类似地，对于CATS，END节点位于S之后，这使得它在trie中成为一个单词。有趣的是，如果像CAT那样在END节点之前放置两个节点，那么我们将在同一路径中存储两个单词，但是可以通过不遍历底部并检查END之间是否存在END来访问CAT。

DOG，DOGS和DOGGO也是这样。对于DOG，我们将只有一个返回值，因为它具有END节点。但是如果我们使用DOG作为前缀搜索贵族，则会得到三个返回值。基本上，这里使用深度优先搜索。

以太坊使用Patricia尝试将交易存储在区块，交易收据中并维护网络状态。

数据存储

为了存储数据对象，我们不需要像单词一样的前缀。由于我们的数据对象是事务或区块，并且我们将用于在特里中存储数据的所有“唯一字符串”将是事务散列或块散列，它们的长度始终相同，因此我们不必担心前缀。

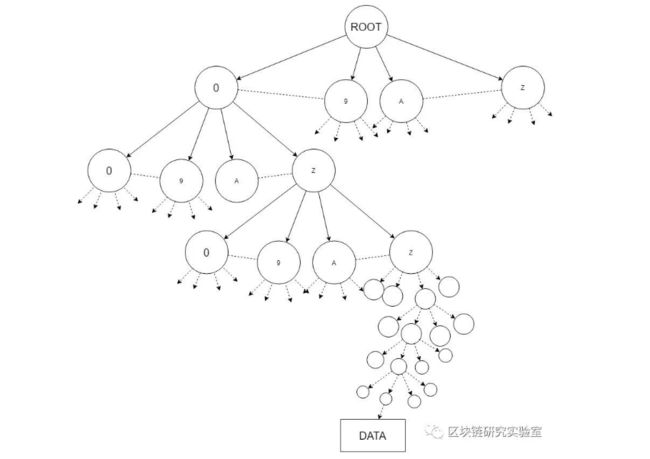
如果我们为事务创建Patricia trie，则它看起来应如下所示，尽管要大得多：

每个交易哈希将具有数字或字符字符（取决于算法）。对于sha256，我们将使用32个字符长的哈希。如果我们假设哈希仅由0–9和A_Z组成，则patricia trie中的每个节点将具有35个子节点。从根开始，我们向下遍历，同时将每个字符与节点值匹配，直到最后获得交易数据对象。

算    法

我们可以说trie中的每个节点本身就是一个哈希表，该哈希表将字符作为键进行哈希，将另一个哈希表作为值进行哈希。所有操作，插入，删除和访问都取O（h），其中h是本例中哈希的长度或树的深度。

通过使用此定义，我们可以编写以下算法在trie中存储数据：

在此算法中，我们创建一个空的键值对对象，遍历哈希的整个长度，并为每个字符设置该值作为新的empyt键值对对象。同样对于每个字符，我们将curr映射设置为下一个映射。最后当我们创建了整个分支时，我们在最后一个节点密钥的标签“ DATA”处设置数据。

在访问时，我们返回键“ DATA”的最后一个映射的值，在删除时，我们只删除给定哈希的叶节点。