LCS算法：最长公共子序列

LCS算法：最长公共子序列定义：
一个序列A任意删除若干个字符得到新序列B，则A叫做B的子序列
两个序列X和Y的公共子序列中，长度最长的那个，定义为X和Y的最长公共子序列
例如：

X={A,B,C,B,D,A,B}
Y={B,D,C,A,B,A}
则它们的lcs分别是
{B,C,B,A}
{B,D,A,B}。
求出一个即可。
LCS的

LCS算法符号表示：

 字符串X,长度m,从1开始计数
 字符串Y,长度n,从1开始计数
 Xi=...,xi>表示X序列的前i个字符(1<=i<=m)
 Yj=...,yj>表示Y序列的前j个字符(1<=j<=n)
 LCS(X,Y)为字符串X和Y的最长公共子序列
 其中的一个解为Z=
 注意:LCS(X,Y)其实为一个集合
 Z为一个解

用递归的思想去做的话，就从大到小从后往前推

            队列X=    A,B,C,B,D,A,B
            队列Y=      B,D,C,A,B,A
            栈A={}
共有两种情况：
1、最后一位相同：{
    ①、X尾去一位，再重新和Y比较
    ②、Y尾去一位，再重新和X比较
    }
2、最后一位相同：
    X、Y分别尾去一位（入栈，最后出栈就是答案），再重新X和Y比较

用动态规划的思想去做，从小到大从前往后推

规则：相同的取左上加1,不同取上和左中的最大值

推导结果如下：

最右下角的值就是答案；

代码实现：
/**
     * 计算最长公共子序列
     * @param strx
     * @param stry
     * @return 最长公共子序列的长度
     */
    public static int lcs(String strx,String stry){
        int row=strx.length()+1;
        int col=stry.length()+1;
        char[] cx=strx.toCharArray();
        char[] cy=stry.toCharArray();
        int[][] arrays=new int[row][col];
        //使用动态规划的方式填入数据
        for (int i = 1; i < arrays.length; i++) {
            for (int j = 1; j < arrays[i].length; j++) {
                int max=0;
                if(cx[i-1]!=cy[j-1]){
                    max=Math.max(arrays[i-1][j], arrays[i][j-1]);
                }else{
                    max=arrays[i-1][j-1]+1;
                }
                arrays[i][j]=max;
            }
        }
        //打印
        for (int i = 0; i < arrays.length; i++) {
            for (int j = 0; j < arrays[i].length; j++) {
                System.out.print(arrays[i][j]+" ");
            }
            System.out.println();
        }
        printLCS(cx,cy,arrays);
        return arrays[row-1][col-1];
    }
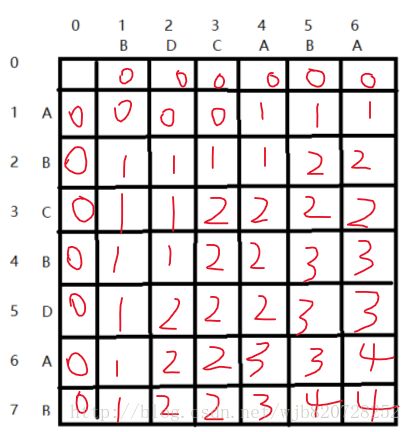
程序运行结果：

0   0   0   0   0   0   0   
0   0   0   0   1   1   1   
0   1   1   1   1   2   2   
0   1   1   2   2   2   2   
0   1   1   2   2   3   3   
0   1   2   2   2   3   3   
0   1   2   2   3   3   4   
0   1   2   2   3   4   4

打印答案的话需要回溯处理：
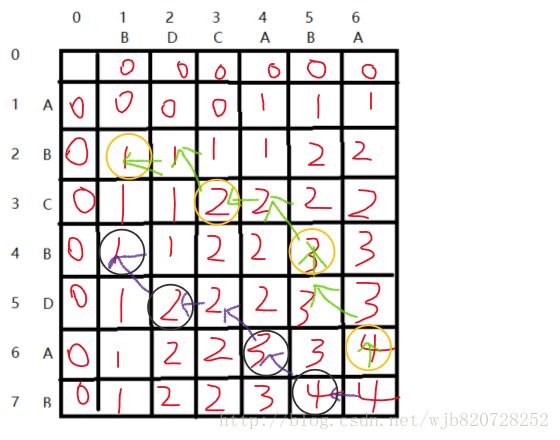
从最后一位回溯：

1、如果i和j 对于的char 不相同，则选上、中最大那个方向走
    如果都一样就代表有多个答案，每个方向就是一个答案，方向：i-1和j   或者  i和j -1

2、如果i和j 对于的char 相同，则就把相应的char入栈，方向：i和j 都分别减一

一直重复1、2操作到轮询结束，打印栈就是答案。


例如：i=7,j=6  value[i][j]=4，4的上、左最大为4，那么尝试从上走（绿色）·····
    栈={A,B,C,B}
    打印结果：
    B,C,B,A

    i=7,j=6  value[i][j]=4，4的上、左最大为4，那么尝试从左走（紫色）·····
    栈={B,A,D,B}
    打印结果：B,D,A,B

推导结果如下：

代码实现：
/**
     * 打印最长公共子序列
     * @param arrays
     */
    public static void printLCS(char[] cx,char[] cy,int[][] arrays){
        Stack stack =new Stack<>();
        int row=arrays.length-1;
        int col=arrays[0].length-1;
        while(row>0&&col>0){
            if(cx[row-1]!=cy[col-1]){
                if(arrays[row-1][col]>=arrays[row][col-1]){
                    row-=1;
                }else if(arrays[row-1][col]1]){
                    col-=1;
                }
            }else{
                stack.push(cx[row-1]+"");
                row-=1;
                col-=1;
            }
        }
        while(!stack.isEmpty()){
            System.out.print(stack.pop()+"  ");
        }
    }

    程序运行结果：

    B   C   B   A   

LCS的应用:
相似度的比较:计算生物学DNA对比(亲子验证)，百度云盘找非法数据(岛国片)
图形相似处理,媒体流的相似比较,百度知道,百度百科，WEB页面中找非法言论等