2.5 矩阵因式分解(第2章矩阵代数)
主要内容
本节首先讲解了LU分解的意义:用来简化线性方程组的计算过程。接着,根据LU分解的形式,得出了求解LU分解的算法。
LU分解的形式和意义
矩阵 A A A的因式分解是把 A A A表示为两个或更多个矩阵的乘积。矩阵乘法是数据的综合(把两个或更多个线性变换的作用结合成一个矩阵),矩阵因式分解是数据分解。在计算机科学中,将 A A A表示为矩阵的乘积对应于对 A A A中数据的预处理过程,把这些数据分成两个或更多个部分,这种结构可能更有用,或者更便于计算。
现实中,有可能会求解一系列系数矩阵 A A A相同,但 b \boldsymbol b b不相同的线性方程:
A x = b 1 , A x = b 2 , . . . , A x = b p A\boldsymbol x = \boldsymbol b_1, \quad A\boldsymbol x = \boldsymbol b_2, \quad ..., \quad A\boldsymbol x=\boldsymbol b_p Ax=b1,Ax=b2,...,Ax=bp
如果能将 A A A预处理为另一种形式,使得每次求解上述任意方程时的计算量减少,那么即使预处理会耗费一些精力,那也是值得的。LU分解就是这样一个预处理过程,通过LU分解,可以使得每一个形如 A x = b A\boldsymbol x = \boldsymbol b Ax=b的方程求解过程变得更为简单。
首先,设 A A A是 m × n m \times n m×n矩阵,它可以行化简为阶梯形而不必进行行对换(后面再考虑一般情形),则 A A A可写成形式 A = L U A=LU A=LU, L L L是 m × m m \times m m×m下三角矩阵,主对角线元素全是 1 1 1, U U U是 A A A的一个 m × n m \times n m×n阶梯形矩阵。 这样一个分解称为LU分解,矩阵 L L L是可逆的,称为单位下三角矩阵。
A = [ 1 0 0 0 ∗ 1 0 0 ∗ ∗ 1 0 ∗ ∗ ∗ 1 ] [ △ ∗ ∗ ∗ ∗ 0 △ ∗ ∗ ∗ 0 0 0 △ ∗ 0 0 0 0 0 ] A = \begin{bmatrix}1 & 0 & 0 & 0 \\* & 1 & 0 & 0 \\ * & * & 1 & 0 \\ * & * & * & 1\end{bmatrix}\begin{bmatrix}\triangle & * & * & * & * \\ 0 & \triangle & * & * & * \\ 0 & 0 & 0 & \triangle & * \\ 0 & 0 & 0 & 0 & 0\end{bmatrix} A=⎣⎢⎢⎡1∗∗∗01∗∗001∗0001⎦⎥⎥⎤⎣⎢⎢⎡△000∗△00∗∗00∗∗△0∗∗∗0⎦⎥⎥⎤
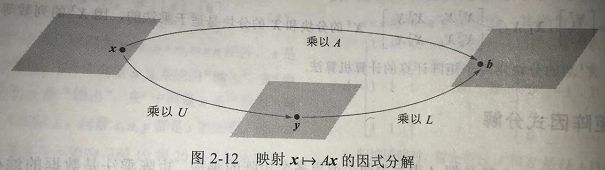
一旦矩阵 A A A可以写成 A = L U A=LU A=LU的形式,方程 A x = b A\boldsymbol x =\boldsymbol b Ax=b可写成 L ( U x ) = b L(U\boldsymbol x)=\boldsymbol b L(Ux)=b,把 U x U\boldsymbol x Ux写成 y \boldsymbol y y,可以解下面一堆方程来求解 x \boldsymbol x x:
L y = b U x = y \begin{aligned}L\boldsymbol y = \boldsymbol b \\ U\boldsymbol x=\boldsymbol y\end{aligned} Ly=bUx=y
首先解 L y = b L\boldsymbol y =\boldsymbol b Ly=b求得 y \boldsymbol y y,然后解 U x = y U\boldsymbol x =\boldsymbol y Ux=y求得 x \boldsymbol x x,由于 L L L和 U U U都是三角矩阵,因此每个方程都比较容易解。
例:
已知:
A = [ 3 − 7 − 2 2 − 3 5 1 0 6 − 4 0 − 5 − 9 5 − 5 − 12 ] = [ 1 0 0 0 − 1 1 0 0 2 − 5 1 0 − 3 8 3 1 ] [ 3 − 7 − 2 2 0 − 2 − 1 2 0 0 − 1 1 0 0 0 − 1 ] = L U A = \begin{bmatrix}3 & -7 & -2 & 2 \\ -3 & 5 & 1 & 0 \\ 6 & -4 & 0 & -5 \\-9 & 5 & -5 & -12\end{bmatrix}=\begin{bmatrix}1 & 0 & 0 & 0 \\-1 & 1 & 0 & 0 \\2 & -5 & 1 & 0 \\-3 & 8 & 3 & 1\end{bmatrix}\begin{bmatrix}3 & -7 & -2 & 2 \\ 0 & -2 & -1 & 2 \\0 & 0 & -1 & 1 \\ 0 & 0 & 0 & -1\end{bmatrix} = LU A=⎣⎢⎢⎡3−36−9−75−45−210−520−5−12⎦⎥⎥⎤=⎣⎢⎢⎡1−12−301−5800130001⎦⎥⎥⎤⎣⎢⎢⎡3000−7−200−2−1−10221−1⎦⎥⎥⎤=LU
应用 A A A的LU分解来解 A x = b A\boldsymbol x = \boldsymbol b Ax=b,其中 b = [ − 9 5 7 11 ] b = \begin{bmatrix}-9 \\ 5 \\7 \\ 11\end{bmatrix} b=⎣⎢⎢⎡−95711⎦⎥⎥⎤
解:
解 L y = b L\boldsymbol y = \boldsymbol b Ly=b仅需6次乘法和6次加法(利用倍乘变换,将第一行利用倍乘变换加到第二、三、四行上,使得第一列主元下的元素都为零,需要三次乘法和三次加法,同理可以计算出处理第二列和第三列主元的运算次数),因为这些运算仅需对第5列进行(在 L L L的每个主元下的零会在行变换的选取中自动产生)。
[ L b ] = [ 1 0 0 0 − 9 − 1 1 0 0 5 2 − 5 1 0 7 − 3 8 3 1 11 ] ∼ [ 1 0 0 0 − 9 0 1 0 0 − 4 0 0 1 0 5 0 0 0 1 1 ] = [ I y ] \begin{bmatrix}L & \boldsymbol b\end{bmatrix} = \begin{bmatrix}1 & 0 & 0 & 0 & -9 \\-1 & 1 & 0 & 0 & 5 \\2 & -5 & 1 & 0 & 7 \\ -3 & 8 & 3 & 1 & 11\end{bmatrix} \sim \begin{bmatrix}1 & 0 & 0 & 0 & -9 \\ 0 & 1 & 0 & 0 & -4 \\ 0 & 0 & 1 & 0 & 5 \\ 0 & 0 & 0 & 1 & 1\end{bmatrix} = \begin{bmatrix}\boldsymbol I & \boldsymbol y\end{bmatrix} [Lb]=⎣⎢⎢⎡1−12−301−5800130001−95711⎦⎥⎥⎤∼⎣⎢⎢⎡1000010000100001−9−451⎦⎥⎥⎤=[Iy]
对 U x = y U\boldsymbol x = \boldsymbol y Ux=y,行化简的向后步骤需要4次除法、6次乘法和6次加法(例如,把 [ U y ] \begin{bmatrix}U & \boldsymbol y\end{bmatrix} [Uy]的第四列变成零需要对第四行做一次除法以使主元变为1,再做三次乘法和加法,以使得第四列上面的元素都变为零)。
[ U y ] [ 3 − 7 − 2 2 − 9 0 − 2 − 1 2 − 4 0 0 − 1 1 5 0 0 0 − 1 1 ] ∼ [ 1 0 0 0 3 0 1 0 0 4 0 0 1 0 − 6 0 0 0 1 − 1 ] \begin{bmatrix}U & \boldsymbol y\end{bmatrix}\begin{bmatrix}3 & -7 & -2 & 2 & -9 \\ 0 & -2 & -1 & 2 & -4 \\ 0 & 0 & -1 & 1 & 5 \\ 0 & 0 & 0 & -1 & 1\end{bmatrix} \sim \begin{bmatrix}1 & 0 & 0 & 0 & 3 \\ 0 & 1 & 0 & 0 & 4 \\ 0 & 0 & 1 & 0 & -6 \\ 0 & 0 & 0 & 1 & -1\end{bmatrix} [Uy]⎣⎢⎢⎡3000−7−200−2−1−10221−1−9−451⎦⎥⎥⎤∼⎣⎢⎢⎡100001000010000134−6−1⎦⎥⎥⎤
因此, x = [ 3 4 − 6 − 1 ] \boldsymbol x = \begin{bmatrix}3 \\ 4 \\-6 \\ -1\end{bmatrix} x=⎣⎢⎢⎡34−6−1⎦⎥⎥⎤
为求 x \boldsymbol x x,需要28次算术运算,不包括求 L L L和 U U U的运算在内。相反, [ A b ] \begin{bmatrix}A & \boldsymbol b\end{bmatrix} [Ab]行化简为 [ I x ] \begin{bmatrix}\boldsymbol I & \boldsymbol x\end{bmatrix} [Ix]需要62次运算(由于存在大量非零元素需要参与运算)。
LU分解算法
设 A A A可以化为阶梯形 U U U,化简过程中仅用行倍加变换,即把一行的倍数加于它下面的另一行。这样,存在单位下三角初等矩阵 E 1 , ⋯ , E p E_1,\cdots,E_p E1,⋯,Ep,使得:
E p ⋯ E 1 A = U E_p \cdots E_1A = U Ep⋯E1A=U
于是,
A = ( E p ⋯ E 1 ) − 1 U = L U A=(Ep \cdots E_1)^{-1}U = LU A=(Ep⋯E1)−1U=LU
其中,
L = ( E p ⋯ E 1 ) − 1 L=(E_p \cdots E_1)^{-1} L=(Ep⋯E1)−1
注意上述过程中的行变换,它把 A A A化为 U U U,所以也把 L L L化为 I \boldsymbol I I,这是因为:
( E p ⋯ E 1 ) L = ( E p ⋯ E 1 ) ( E p ⋯ E 1 ) − 1 = I (E_p \cdots E_1)L = (E_p \cdots E_1)(E_p \cdots E_1)^{-1} = \boldsymbol I (Ep⋯E1)L=(Ep⋯E1)(Ep⋯E1)−1=I
这一点是构造 L L L的关键。
下面是LU分解的算法:
- 如果可能的话,用一系列的行倍加变换把 A A A化为阶梯形 U U U
- 填充 L L L的元素,使得相同的行变换把 L L L变为 I \boldsymbol I I
由于 ( E p ⋯ E 1 ) L = I (E_p \cdots E_1)L = \boldsymbol I (Ep⋯E1)L=I,于是,根据可逆矩阵定理, L L L是可逆的, ( E p ⋯ E 1 ) = L − 1 (Ep \cdots E_1)=L^{-1} (Ep⋯E1)=L−1
例:
求下列矩阵的LU分解:
A = [ 2 4 − 1 5 − 2 − 4 − 5 3 − 8 1 2 − 5 − 4 1 8 − 6 0 7 − 3 1 ] A=\begin{bmatrix}2 & 4 & -1 & 5 & -2 \\ -4 & -5 & 3 & -8 & 1 \\2 & -5 & -4 & 1 & 8 \\-6 & 0 & 7 & -3 & 1\end{bmatrix} A=⎣⎢⎢⎡2−42−64−5−50−13−475−81−3−2181⎦⎥⎥⎤
解:
因 A A A有4行,故 L L L应为 4 × 4 4 \times 4 4×4矩阵。 L L L的第一列应该是 A A A的第一列除以它的第一行主元元素:
L = [ 1 0 0 0 − 2 1 0 0 1 ∗ 1 0 − 3 ∗ ∗ 1 ] L = \begin{bmatrix}1 & 0 & 0 & 0 \\ -2 & 1 & 0 & 0 \\ 1 & * & 1 & 0 \\ -3 & * & * &1\end{bmatrix} L=⎣⎢⎢⎡1−21−301∗∗001∗0001⎦⎥⎥⎤
比较 A A A和 L L L的第一列。把 A A A的第一列的后三个元素变成零的行变换(这是将 A A A化为 U U U的第一阶段)同时也将 L L L的第一列的后三个元素变成0(根据定义, L L L的主对角线元素均为 1 1 1)。同样的道理对 L L L的其他各列也是成立的。因此,一旦知道了将 A A A化为 U U U的过程,再根据 L L L的主对角线元素均为 1 1 1,以及将 A A A化为 U U U的过程和将 L L L化为 I \boldsymbol I I的过程是一致的,自然就能够推算出 L L L中的各个元素。
下面是将 A A A行化简为 U U U的过程:
A = [ 2 4 − 1 5 − 2 − 4 − 5 3 − 8 1 2 − 5 − 4 1 8 − 6 0 7 − 3 1 ] ∼ [ 2 4 − 1 5 − 2 0 3 1 2 − 3 0 − 9 − 3 − 4 10 0 12 4 12 − 5 ] ∼ [ 2 4 − 1 5 − 2 0 3 1 2 − 3 0 0 0 2 1 0 0 0 4 7 ] ∼ [ 2 4 − 1 5 − 2 0 3 1 2 − 3 0 0 0 2 1 0 0 0 0 5 ] = U \begin{aligned}A &= \begin{bmatrix}\boldsymbol 2 & 4 & -1 & 5 & -2 \\ \boldsymbol {-4} & -5 & 3 & -8 & 1 \\ \boldsymbol 2 & -5 & -4 & 1 & 8 \\ \boldsymbol {-6} & 0 & 7 & -3 & 1\end{bmatrix} \\ &\sim \begin{bmatrix}2 & 4 & -1 & 5 & -2 \\ 0 & \boldsymbol 3 & 1 & 2 & -3 \\ 0 & \boldsymbol {-9} & -3 & -4 & 10 \\ 0 & \boldsymbol {12} & 4 & 12 & -5\end{bmatrix} \\ &\sim \begin{bmatrix}2 & 4 & -1 & 5 & -2 \\ 0 & 3 & 1 & 2 & -3 \\0 & 0&0 & \boldsymbol 2 & 1 \\ 0 & 0& 0 & \boldsymbol 4 & 7\end{bmatrix} \\&\sim\begin{bmatrix}2 & 4 & -1 & 5 & -2 \\ 0 & 3 & 1 & 2 & -3 \\ 0 & 0 & 0 & 2 & 1 \\0 & 0 & 0 & 0 & \boldsymbol 5\end{bmatrix} = U \end{aligned} A=⎣⎢⎢⎡2−42−64−5−50−13−475−81−3−2181⎦⎥⎥⎤∼⎣⎢⎢⎡200043−912−11−3452−412−2−310−5⎦⎥⎥⎤∼⎣⎢⎢⎡20004300−11005224−2−317⎦⎥⎥⎤∼⎣⎢⎢⎡20004300−11005220−2−315⎦⎥⎥⎤=U
上式中标出的元素确定了将 A A A化为 U U U的行化简。在每个主元列,把标出的元素除以主元后将结果放入 L L L:
L = [ 1 0 0 0 − 2 1 0 0 1 − 3 1 0 − 3 4 2 1 ] L = \begin{bmatrix}1 & 0 & 0 & 0 \\ -2 & 1 & 0 & 0 \\ 1 & -3 & 1 & 0 \\ -3 & 4 & 2 & 1\end{bmatrix} L=⎣⎢⎢⎡1−21−301−3400120001⎦⎥⎥⎤
上述只讨论了没有行对换参与的情况。实际应用中,肯定会使用到行对换,这是完全可以做到的,但这里略去不详述。