推荐算法_03_FM算法论文

Abstract—In this paper, we introduce Factorization Machines (FM) which are a new model class that combines the advantages of Support Vector Machines (SVM) with factorization models. Like SVMs, FMs are a general predictor working with any real valued feature vector. In contrast to SVMs, FMs model all interactions between variables using factorized parameters. Thus they are able to estimate interactions even in problems with huge sparsity (like recommender systems) where SVMs fail. We show that the model equation of FMs can be calculated in linear time and thus FMs can be optimized directly. So unlike nonlinear SVMs, a transformation in the dual form is not necessary and the model parameters can be estimated directly without the need of any support vector in the solution. We show the relationship to SVMs and the advantages of FMs for parameter estimation in sparse settings.
           在本文中，我们介绍了因子分解机（FM），它是一种新的模型类，它结合了支持向量机（SVM）和因式分解模型的优点。与SVM一样，FM是使用任何实值特征向量的能用预测器。与SVM相比，FM使用分解参数模拟变量之间的所有交互。因此，即使在SVM失败的巨大稀疏性（如推荐系统）的问题中，他们也能够估计相互作用。我们证明了FM的模型方程可以在线性时间内计算，因此FM可以直接优化。因此，与非线性SVM不同，不需要双重形式的变换，并且可以直接估计模型参数，而无需解决方案中的任何支持向量。我们展示了与SVM的关系以及FM在稀疏设置中进行参数估计的优势。

           On the other hand there are many different factorization models like matrix factorization, parallel factor analysis or specialized models like SVD++, PITF or FPMC. The drawback of these models is that they are not applicable for general prediction tasks but work only with special input data. Furthermore their model equations and optimization algorithms are derived individually for each task. We show that FMs can mimic these models just by specifying the input data (i.e. the feature vectors). This makes FMs easily applicable even for users without expert knowledge in factorization models.
           Index Terms—factorization machine; sparse data; tensor fac- torization; support vector machine
           另一方面，有许多不同的因子分解模型，如矩阵分解，并行因子分析或专用模型，如SVD ++，PITF或FPMC。这些模型的缺点是它们不适用于能用的预测任务，但仅适用于特殊输入数据。此外，他们的模型方程和优化算法是针对每个任务单独导出的。FM仅通过指定输入数据（即特征向量）就可以模拟这些模型。这使得即使对于没有分解模型专业知识的用户，FM也很容易适用。
          索引术语：分解机；稀疏数据；张量因子化；支持向量机

I. INTRODUCTION

        Support Vector Machines are one of the most popular predictors in machine learning and data mining. Nevertheless in settings like collaborative filtering, SVMs play no important role and the best models are either direct applications of standard matrix/ tensor factorization models like PARAFAC [1] or specialized models using factorized parameters [2], [3], [4]. In this paper, we show that the only reason why standard SVM predictors are not successful in these tasks is that they cannot learn reliable parameters (‘hyperplanes’) in complex (non-linear) kernel spaces under very sparse data. On the other hand, the drawback of tensor factorization models and even more for specialized factorization models is that (1) they are not applicable to standard prediction data (e.g. a real valued feature vector in Rn.) and (2) that specialized models are usually derived individually for a specific task requiring effort in modelling and design of a learning algorithm.
        支持向量机是机器学习和数据挖掘中最受欢迎的预测器之一。 然而，在协同过滤等环境中，SVM并不起重要作用，最好的模型要么是直接应用于标准矩阵/张量分解模型，如PARAFAC [1]，要么是使用分解参数[2]，[3]，[4]的专用模型。 在本文中，我们表明标准SVM预测器在这些任务中不成功的唯一原因，是它们无法在非常稀疏的数据下学习复杂（非线性）内核空间中的可靠参数（“超平面”）。 另一方面，张量因子分解模型，甚至专门分解模型的缺点是（1）它们不适用于标准预测数据（例如Rn中的实值特征向量）和（2）专用模型是 通常为需要在学习和设计学习算法方面付出努力的特定任务单独导出。

        In this paper, we introduce a new predictor, the Factorization Machine (FM), that is a general predictor like SVMs but is also able to estimate reliable parameters under very high sparsity. The factorization machine models all nested variable interactions (comparable to a polynomial kernel in SVM), but uses a factorized parametrization instead of a dense parametrization like in SVMs. We show that the model equation of FMs can be computed in linear time and that it depends only on a linear number of parameters. This allows direct optimization and storage of model parameters without the need of storing any training data (e.g. support vectors) for prediction. In contrast to this, non-linear SVMs are usually optimized in the dual form and computing a prediction (the model equation) depends on parts of the training data (the support vectors). We also show that FMs subsume many of the most successful approaches for the task of collaborative filtering including biased MF, SVD++ [2], PITF [3] and FPMC [4].
        在本文中，我们引入了一种新的预测器，即因子分解机（FM），它是像SVM一样的通用预测器，但也能够在非常高度的稀疏下估计可靠的参数。FM模拟所有嵌套变量交互（与SVM中的多项式内核相比），但使用分解参数化而不是像SVM中那样的密集参数化。我们证明了FM的模型方程可以在线性时间内计算O(kn)，并且它仅取决于线性数量的参数。这允许直接优化和存储模型参数，而无需存储任何用于预测的训练数据（例如，支持向量）。与此相反，非线性SVM通常以双重形式进行优化，并且计算预测（模型方程）取决于训练数据的部分（支持向量）。我们还表明，FM包含许多最成功的协同过滤任务方法，包括偏置MF，SVD ++ [2]，PITF [3]和FPMC [4]。

In total, the advantages of our proposed FM are:
1) FMs allow parameter estimation under very sparse data where SVMs fail.
2) FMs have linear complexity, can be optimized in the primal and do not rely on support vectors like SVMs. We show that FMs scale to large datasets like Netflix with 100 millions of training instances.
3) FMs are a general predictor that can work with any real valued feature vector. In contrast to this, other state-of- the-art factorization models work only on very restricted input data. We will show that just by defining the feature vectors of the input data, FMs can mimic state-of-the-art models like biased MF, SVD++, PITF or FPMC.
总的来讲，FM有如下优点：
1. FM在高度稀疏数据下参数估计表现良好，而SVM则不行；
2. FM具有线性时间复杂度O(kn)，可以在原始中进行优化，不用像SVM那样依赖支持向量。 我们展示了FM可以扩展到像Netflix这样拥有1亿个训练实例的大型数据集。
3. FM是一种可以与任何实值特征向量一起使用的通用预测器。 与此相反，其他最先进的分解模型仅适用于非常有限的输入数据。 我们将展示仅通过定义输入数据的特征向量，FM可以模拟最先进的模型，如偏置MF，SVD ++，PITF或FPMC。

FM三板斧：线性时间复杂度O(kn)、高度稀疏数据下表现良好、通用预测器

II. PREDICTION UNDER SPARSITY

        The most common prediction task is to estimate a function y: →T from a real valued feature vector x∈ to a target domain T (e.g. T = R for regression or T = {+, −} for classification). In supervised settings, it is assumed that there is a training dataset D = {, . . .} of examples for the target function y given. We also investigate the ranking task where the function y with target T = R can be used to score feature vectors x and sort them according to their score. Scoring functions can be learned with pairwise training data [5], where a feature tuple (, ) ∈ D means that  should be ranked higher than . As the pairwise ranking relation is antisymmetric, it is sufficient to use only positive training instances.
        最常见的预测任务是估计一个函数
                                             y： → T
该函数将一个n维的实值特征向量，映射到一个目标域。（例如，对于回归问题，对于分类问题 T = {+, -}）
在监督学习场景中，通常有一个带标签的训练数据集：

                                             

其中 表示输入数据，对应样本的特征向量， 是标签，n是样本数目。
我们还研究了排名任务，其中具有目标T = R的函数y可用于对特征向量x进行评分，并根据其得分对它们进行排序。 评分函数可以用成对训练数据[5]学习，其中特征元组表示应该排名高于。 由于成对排序关系是反对称的，因此仅使用积极的训练实例就足够了。

        In this paper, we deal with problems where x is highly sparse, i.e. almost all of the elements xi of a vector x are zero. Let m(x) be the number of non-zero elements in the feature vector x and mD be the average number of non-zero elements m(x) of all vectors x ∈ D. Huge sparsity (mD ≪ n) appears in many real-world data like feature vectors of event transactions (e.g. purchases in recommender systems) or text analysis (e.g. bag of word approach). One reason for huge sparsity is that the underlying problem deals with large categorical variable domains.
        在本文中，我们处理的特征向量是高度稀疏的，即向量的几乎所有元素都为零。 设是特征向量中的非零元素的数量，是向量x∈D中所有非零元素的平均数。高度稀疏性（ « n）出现在许多中 现实世界数据，如事件交易的特征向量（例如，推荐系统中的购买）或文本分析（例如，词汇方法）。巨大稀疏性的一个原因是潜在的问题涉及大的分类变量域。

Example 1 Assume we have the transaction data of a movie review system. The system records which user u ∈ U rates a movie (item) i ∈ I at a certain time t ∈ R with a rating r ∈ {1, 2, 3, 4, 5}. Let the users U and items I be:
                                U = {Alice (A), Bob (B), Charlie (C), . . .}
                                 I = {Titanic (TI), Notting Hill (NH), Star Wars (SW), Star Trek (ST), . . .}
Let the observed data S be:
                               S = {(A, TI, 2010-1, 5),(A, NH, 2010-2, 3),(A, SW, 2010-4, 1), (B, SW, 2009-5, 4),(B, ST, 2009-8, 5), (C, TI, 2009-9, 1),(C, SW, 2009-12, 5)}
An example for a prediction task using this data, is to estimate a function yˆ that predicts the rating behaviour of a user for an item at a certain point in time.
        在这里，我们以电影评分系统为例，举一个高度稀疏数据的例子。
        在电影评分系统中，记录着用户，在某个时间，对某个电影，做出评分。假设用户集U和电影集I分别如下：
                           U = {Alice (A), Bob (B), Charlie (C), . . .}
                           I = {Titanic (TI), Notting Hill (NH), Star Wars (SW), Star Trek (ST), . . .}
设观测到的数据集S如下：
                           S = { (A, TI, 2010-1, 5),  //表示Alice在2010年1月，对电影Titanic评分5分
                                   (A, NH, 2010-2, 3),
                                   (A, SW, 2010-4, 1),
                                   (B, SW, 2009-5, 4),
                                   (B, ST, 2009-8, 5),
                                   (C, TI, 2009-9, 1),
                                   (C, SW, 2009-12, 5)}
利用观测数据集S，来进行预测任务的一个实例是：估计一个函数，来预测某个用户在某个时间，对某部电影的打分行为。

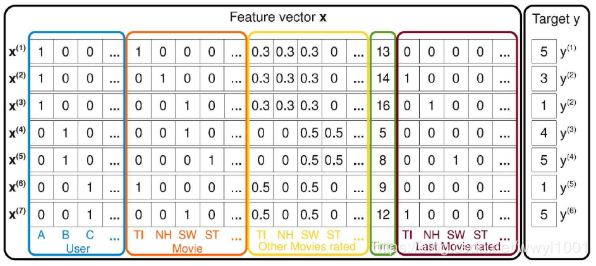
Figure 1 shows one example of how feature vectors can be created from S for this task. Here, first there are |U| binary indicator variables (blue) that represent the active user of a transaction – there is always exactly one active user in each transaction (u, i, t, r) ∈ S, e.g. user Alice in the first one (x (1) A = 1). The next |I| binary indicator variables (red) hold the active item – again there is always exactly one active item (e.g. x (1) TI = 1). The feature vectors in figure 1 also contain indicator variables (yellow) for all the other movies the user has ever rated. For each user, the variables are normalized such that they sum up to 1. E.g. Alice has rated Titanic, Notting Hill and Star Wars. Additionally the example contains a variable (green) holding the time in months starting from January, 2009. And finally the vector contains information of the last movie (brown) the user has rated before (s)he rated the active one – e.g. for x (2) , Alice rated Titanic before she rated Notting Hill. In section V, we show how factorization machines using such feature vectors as input data are related to specialized state-of-the-art factorization models.
We will use this example data throughout the paper for illustration. However please note that FMs are general predictors like SVMs and thus are applicable to any real valued feature vectors and are not restricted to recommender systems.
        上图是由观测集S构造的特征向量和标签的例子，如第一条观测记录中，Alice对Titanic的评分是5。特征向量由五个部分组成：

1. 蓝色方框：表示评分用户信息，维度是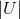，在该部分分量中，当前电影评分用户所在位置为1，其它为0。例如，在第一条观测记录中，有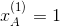，表示当前评分用户是Alice。
2. 橙色方框：表示被评分电影信息，维度是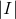，在该部分分量中，当前被评分的电影所在位置为1，其它为0。例如，在第一条观测记录中，有 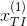= 1，表示当前被评分电影是Titanic。
3. 黄色方框：表示当前评分用户评分过的所有电影信息，维度是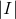，在该部分分量中，被当前用户评分过的所有电影的位置为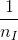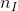（是所有评分过的电影数目），其它为0。例如，Alice评分过电影TI，NH和SW，那么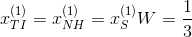
4. 绿色方框：表示评分日期信息，维度是1。基数是2009年1月，以后每增加1个月就加1，例如2009年5月可表示为5。
5. 棕色方框：表示当前评分用户最近评分过的一部电影信息，维度是。

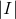在第五节中，我们展示了使用这些特征向量作为输入数据的分解机器如何与专门的现有分解模型相关联。我们将在整篇论文中使用此示例数据进行说明。 但请注意，同SVM一样，FM是一般预测器，因此适用于任何实值特征向量，不限于推荐系统。

III. FACTORIZATION MACHINES (FM)
        本节将介绍FM模型。我们详细的讨论模型方程，并且简单介绍FM在一些预测任务上的应用。

1. FM模型
1.1 模型方程：
FM二阶表达式如下：
               
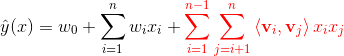
其中，， (n维向量)，
 (n*k的矩阵)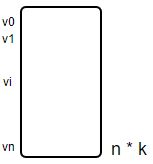，，k是超参数，表示分解的维度。

而，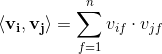
FM的二阶模型，能够表达特征变量的独自和两两间的交互相系。
是全局偏置
是第i个特征变量的权重
模拟了特征变量与的交互，而不是直接用一个简单的实数表示权重。

1.2 表达能力
有定理指出“当k足够大时，对于任意一个正定矩阵，均存在矩阵，使得”。理论分析中，参数k要足够大，但是在高度稀疏数据场景中，由于没有足够的样本来估计复杂的交互矩阵，通常k取得很小。对参数k（即FM的表达能力）的限制，可以得到更好的泛化能力。

1.3 稀疏下的参数估计
在稀疏场景中，通常没有足够多的数据直接独立的来评估特征变量间的交互性。但是FM可以应付这种场景，它是通过分解的方式。举例：在测试集S中，没有Alice对电影Star Trek的评分记录，如果要直接估计Alice和Star Trek之间（即和）的相互关系，显然得到系数。但是在FM中，用分解的交互参数可以评估

1.4 计算
在1.1中公式中，FM方程式的时间复杂度是，可以通过公式优化把时间复杂度降低为

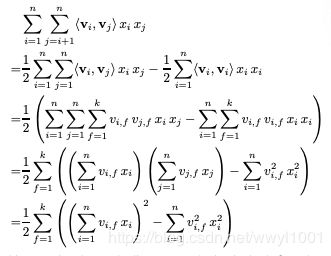
2. FM在预测任务中的应用

• 回归问题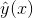：可以直接做为预测值，优化目标是最小化损失函数，如最小化圴方误差。
• 二分类问题：损失函数通常用hinge lost或logit loss
• 排序问题：

通常，我们要在损失函数中加上正则项，目的是为了防止过拟合。（正则项的通俗理解是：是为了保证参数波动小，不会出现部分参数特别大，部分参数特别小的情况）

3. 学习算法
 

参考：
FM算法解析

推荐系统召回四模型之：全能的FM模型