RecastNavigation-NavMesh生成原理
本文翻译自CritterAI的文档:http://critterai.org/projects/cainav/doc/html/e72bd1ee-04b0-4bbb-a21d-d8d7ecaa11af.htm
RecastNavigation是一款非常强大的寻路系统,被广泛的应用于各大游戏引擎中。如Unreal,Unity等。我之前也尝试看过部分RecastNavigation源码,添加了一些注释,放到了我自己的github上(https://github.com/youlanhai/recastnavigation-learn)。
CritterAI是基于RecastNavigation原理开发的一套寻路系统,因此理解了CritterAI也就相当于理解了RecastNavigation。因为RecastNavigation的学习资料比较少,当我看到这篇文章的时候,觉得能够帮助我们去深入理解RecastNavigation,所以就翻译下来跟大家分享,有翻译不当的地方尽请指正。以下是原文翻译:
概述
本篇文章介绍了NMGen的核心处理流程。NMGen用于生成多边形数据,代表了导航网格的表面。有很多种网格生成方式,但是他们都包含了下面的一些步骤。
大体流程如下:
1. 体素化。从源几何体构造实心的高度场,用来表示不可行走的空间。
2. 生成地区。将实心高度场的上表面中连续的区间合并为地区。
3. 生成轮廓。检测地区的轮廓,并构造成简单多边形。
4. 生成多边形网格。将轮廓分割成凸多边形。
5. 生成高度细节。将多边形网格三角化,得到高度细节。
体素化(Voxelization)
核心类:Heightfield
在体素1化阶段,源几何体被转换成高度场,用来表示不可行走的空间。一些不可走的表面在这个阶段会被剔除掉2。
对于源几何体上的每个三角形,使用“保守体素化算法”(Conservative Voxelization)分割成体素,并加入到高度场中。保守体素化算法确保了每个三角形面,都会被生成的体素完全包围。
体素化阶段后,实心高度场(solid heightfield)包含了很多的区间(span),覆盖了源几何体上的所有面。
生成地区(Region Generation)
核心类:CompactHeightfield
这一阶段的目标是,近一步定义实体表面上哪部分是可以行走的,以及将这些可行走的部分划分成连续的地区,这些地区可以最终构成简单多边形。
首先,将实心的高度场,转换成一个开放的高度场(open heightfield),用来表示实体表面上那些可以行走的部分。一个开放的高度场,表示位于实体空间表面的地表部分。
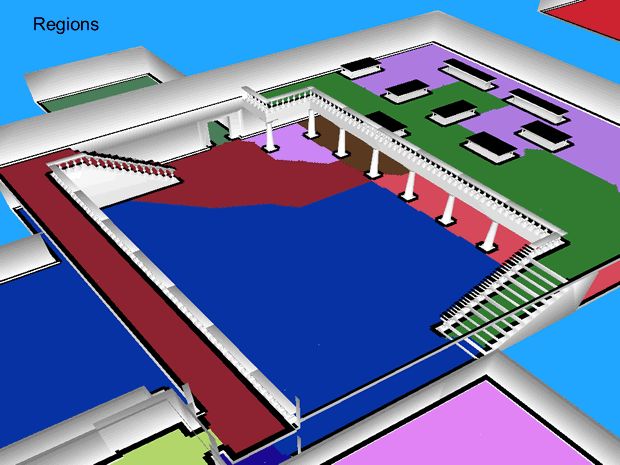
在下图中,绿色部分代表开放区间(span)中的地表。这相当于是实心高度场上所有可行走的上表面。注意那些墙,桌子下面的区域,以及走廊扶手上那些比较窄的区域,已经在实心高度场生成的时候被剔除掉了。一些不可行走的区域,比如桌面3,楼梯扶手,墙边较窄的位置,目前仍然显示为可行走的。
然后,进一步剔除掉不可行走的区域。在计算完成的时候,开放区间中那些认为可以行走的部分,应该通过下面的测试:
+ 该区域不能紧挨着障碍物(如,墙,家具等)(使用WalkableRadius作为距离阀值)
+ 该区域在表面之上没有足够的开放空间(非碰撞区域)。(人在不碰撞到其他物体的情况下,能够合法的移动)(使用WalkableHeight作为高度阀值)
为剩下的所有区间生成邻接信息,用于把他们合并成一个大的面片。该算法使用一个最大垂直步长(WalkableStep4)来决定哪些区间是可以连在一起的。这允许一些特殊的结构能够被考虑进来,比如楼梯,路边,桌面等。例如,构成阶梯的区间能够当做邻居被连接在一起,而桌面上的区间就不能和地板连接在一起。
下图显示的是地区。注意看阶梯上的那些地区,尽管构成的区间并没有直接相连。也需要注意那些桌子上,楼梯扶手,以及所有其他实心高度场上不可走的面,在这个阶段后已经被成功剔除了(黑色表示被剔除的区间)。
在该阶段后,这些相连的地区代表了可行走的面。
生成轮廓(Contour Generation)
核心类:ContourSet
轮廓就是沿着地区边缘“行走”,构成简单多边形。这是从体素空间转换回向量空间的第一步处理。
首先,从地区生成非常精细的多边形。
然后,使用多种算法来完成下面的步骤:
+ 简化相邻多边形的边缘(地区之间的部分)
+ 简化边界(边界是没有邻接或邻接了障碍物的轮廓)(EdgeMaxDeviation)
+ 优化边界的长度。(边界如果太长,不能得到最优的三角形)
下图展示了执行此算法后的轮廓
在该阶段结尾,简单多边形代表了可行走的表面。
生成凸多边形(Convex Polygon Generation)
核心类:PolyMesh
许多算法只能用于凸多边形。因此,这一步需要把轮廓构成的简单多边形转换成凸多边形网格。
注意:许多寻路算法都使用这个网格
下图中,你可以看到由轮廓形成的凸多边形。
在该阶段的结尾,一个凸多边形网格代表了可以行走的表面。
生成高度细节(Height Detail Generation)
核心类:PolyMeshDetail
在这最后的阶段,凸多边形网格会被Delaunay三角化算法三角化,于是可以增加高度的细节。在多边形的内部或者边缘添加顶点,来确保网格与原始几何体表面等价。(DetailSampleDistance和DetailMaxDeviation)
注意:从技术上讲,这一步是可缺省的。细节网格在寻路中不是必须的,但是存在细节网格的情况下,某些查询会返回更加精确的数据。
- 译注:体素是空间中的一个有大小的点,实际上就是一个AABB。 ↩
- 译注:比如坡度过大的面 ↩
- 译注:这里应该是指比较矮的桌子,高度介于MaxClampHeight和WalkableHieght之间。 ↩
- 译注:recastnavigation代码中用的是walkableClimb变量。 ↩