数据分析中缺失值处理~R语言

最近接到了一些真实的数据，数据中包含着许多缺失值，如何对缺失值处理，能更好的为我们做数据分析，更高效率的建模，缩小在测试集上预测分析的偏差，当然这个偏差越小我们肯定越高兴的。

数据准备

我用的是一份地理样本数据，里面有坐标，各种物质成分（Ca，N，P等）

对于缺失数据的检验，有多个方法。

第一种：

library(VIM)

aggr(env,prop=T,numbers=T)

函数用法，可以在控制台加载完包后help()或者?函数

一看这数据还不算崩溃，但是缺失还是比较严重的，

第二种方法：

用mice包中的md.pattern（data）

怎么解读这个呢，其实最后一行返回的就是缺失数目，98为一共有多少缺失值。

缺失值的处理方法有哪些呢？我主要是做笔记

1、删除缺失值

 其实这种方法只有在自己拥有大量的数据进行模型训练才可以选择删除，比如用na.omit()或者

在建模时设置na.action=na.omit。当然，实际业务在过手的时候，数据量不大的情况下，或者你删除

缺失值后，建立的模型不能很好的解释业务，可以考虑缺失值的重新认定。

2、删除个别变量

 对于有些确实很严重的数据，比如缺失值的数量超过了你在业务上认定的比例，那么可以删除这个变量。但是我最近接到的数据居然是长这样的，就是这个变量对于要建立的模型很重要，在不能

删除这个变量，我们需要考量变量在模型中的地位以及训练和测试的数量上做一抉择。

3、用普通的方法进行插值

 为什么我要说普通的方法呢？使用我稍后举例的方法进行插值，这种方法略显粗糙，我并不否定

这些方法，每一种方法都有其存在的应用场景。

library(Hmisc)

impute(env$Ca,mean)        ####平均值
impute(env$K,median)       ####中位数
impute(env$P,zs)          ####众  数 这里的zs<-MS(env$P)
impute(env$N,"random")      ####随  机

当然在e1071里面也有这函数。还有

众数是需要自己计算的

MS <- function(x){ return(as.numeric(names(table(x))[table(x) == max(table(x))]))}

当然你要直接采用这种方法进行插补数据，

env$Ca<-impute(env$Ca,mean)       ####平均值，适用于接近正态分布
env$K<-impute(env$K,median)       ####中位数，偏态不是很严重
env$P<-impute(env$P,zs)         ####众  数
env$N<-impute(env$N,"random")     ####随  机

这样就将数据生成一个完整的数据集了。分析的事情就可以继续走了。祝好运！

当然不管怎样，这样的数据生成的是否合理？怎么去检验我插补的数据是否客观呢或者近乎合理呢？

此时，我们需要计算插值的精度。我们需要引进DMwR包install.packages("DMwR")，library(DMwR)

提到这个包，里面有manyNAs(data,0.2)这么个函数返回的是找出缺失值大于列数20%的行，这个0.2是可

以调的。

在计算插补效果需要用到DMwR包的regr.eval（）函数

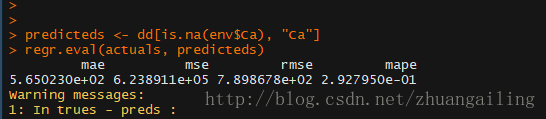
4、在DMwR包里有centralImputation（）这个函数是利用数据的中心趋势值来填补缺失值。

看下和原始数据的差距，这儿我用的是PerformanceAnalytics包的chart.Correlation（）函数

上图是用centralImputation（）函数插补后的分布，看一下插补效果

mape值比前面普通方法还大了，看来效果不咋的啊

再看一下源数据

总的来讲，没有影响到相关性，还有大致的分布。

5、K最近邻法

在DMwR包中的knnImputation（）函数是基于欧氏距离找到K个与其最近的观测数值，然后对这K个近邻的数据利用距离逆加权得到插补的值，然后替代了源数据中的缺失值。

knnoutput <- knnImputation(env) 

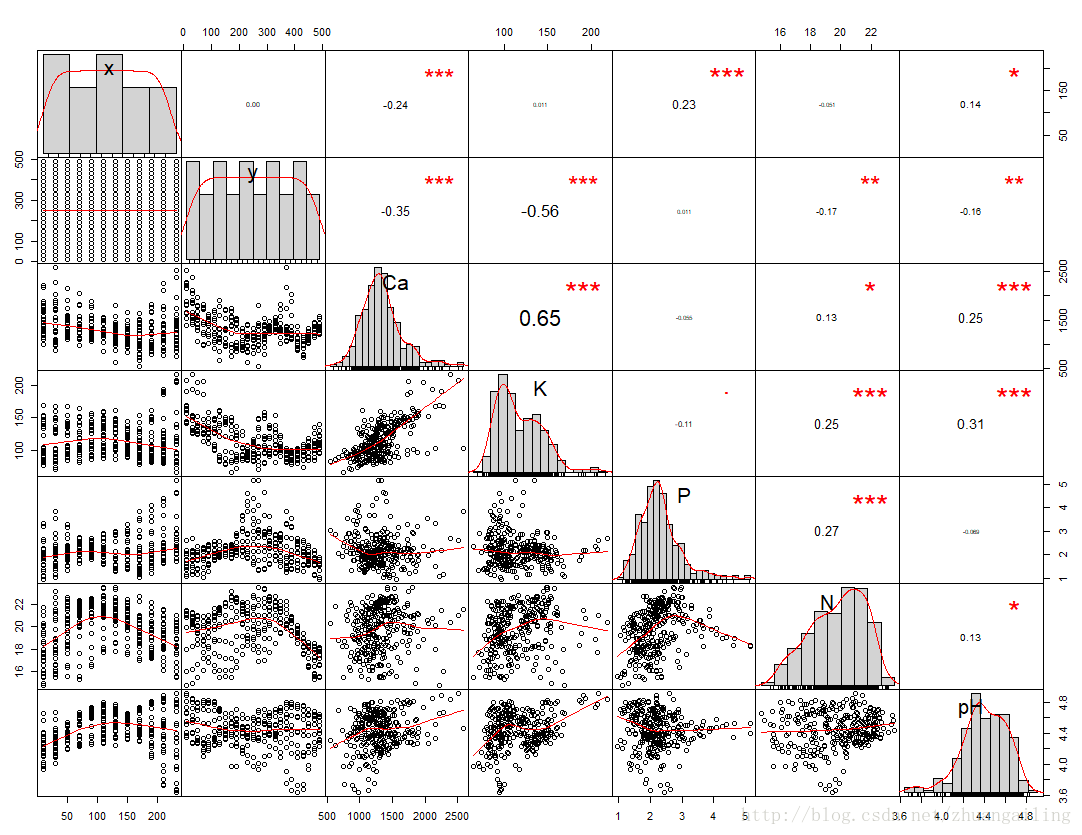
这下显得略有可怕的地方，只是轻微改变了相关系数的值，有的还没有被改变，而且变量的相关性仅仅有细微的差别。

我们看mape值是下降了的，看来插补效果是实在的在提升啊。

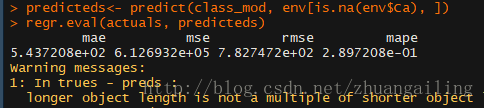
6、rpart

使用决策树来预测缺失值，它相对于前面的优点是能够对因子类变量进行插补，centralImputation（）函数也是可以的，

不过对于名义型变量它采取的是众数。

使用rpart（）函数对于数值型变量（method=anova），因子型变量（method=class）。需要注意method的使用方法

看了下，效果没有K最邻近法好啊。

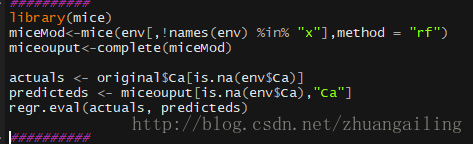
7、mice

这个主要是利用mice（）函数进行建模，利用complete（）函数再生成完整的数据

看到代码，mice在建模的时候用的是随机森林。最后计算了下插补效果，不行呐。

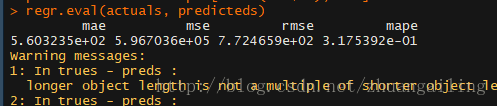
然后我把method的参数改成method="norm"(正态分布）

然后我计算了一下插补效果，大不如人意啊，因为我们从源数据的分布看缺失指标并不

成正态分布，所以我能理解。

对mice（）换个用法，继续

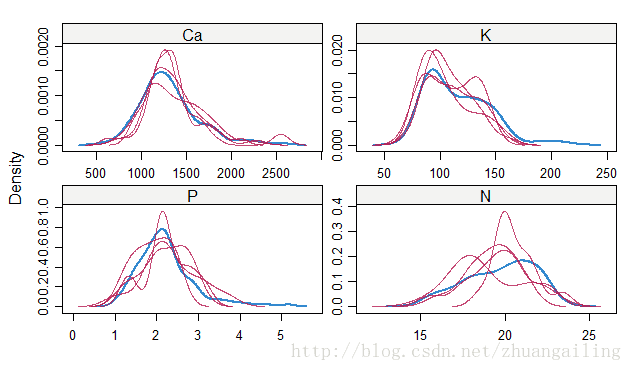
我看看我的插补效果，此时我比较喜欢lattice包中的densityplot()函数

看了下，对N的预测还不是很好，但趋势预测还是蛮可以的。其他变量的缺失预测分析还是不错。

8、还有的包和方法

包	大致描述
Hmisc	对多种函数，支持简单插补、多重插补和典型变量插补
longitudinalData	对时间序列缺失值进行插补的一系列函数
pan	多元面板数据或着聚类的多重插补
kmi	处理生存分析缺失值的Kaplan-Meier的多重插补
cat	在对数线性模型中带有多元类别型变量的多重插补
mvnmle	对多元正态颁数据中缺失值的最大似然估计
。。。	。。。

这是目前本人接触过的，部分我已经用过的，再继续补充。

9、回到问题的本身

对缺失值处理，不同的数据源和不同的业务要求，采用的方法肯定是不一样的，当然需要我们在对缺失值处理的过程中保持客观的判断，加油。