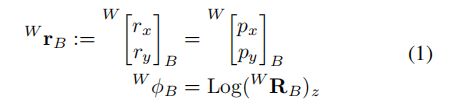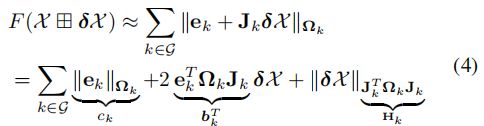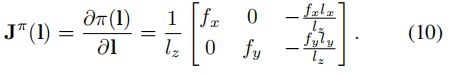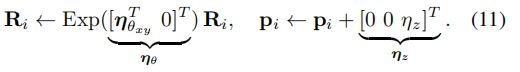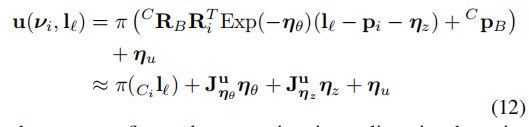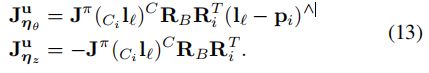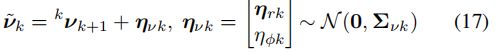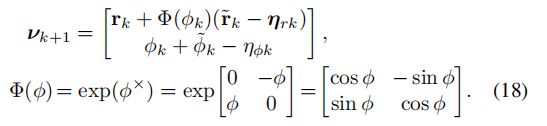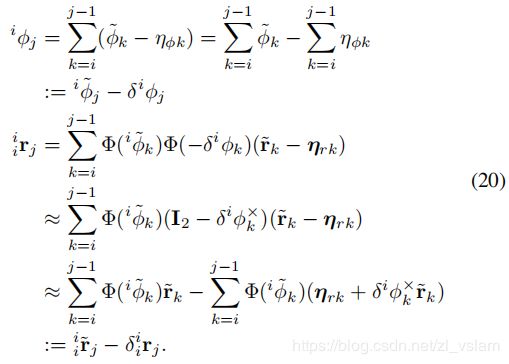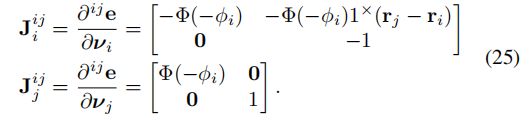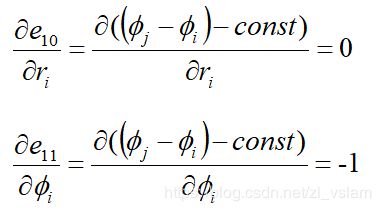视觉融合里程计SLAM算法SE2Lam解析-论文篇

解析论文名称是：Visual-Odometric Localization and Mapping for Ground Vehicles Using SE(2)-XYZ Constraints

代码的github地址是：https://github.com/izhengfan/se2lam

时隔多年，其实也没几年，决定开始写第二篇博客，选择该主题的原因是，在研究IMU预积分的时候，很多地方都存在疑问，但是轮式odometry不一样，首先从应用就可以得知，是二维平面约束，二维形式非常简单，里程计的噪声及残差公式也极容易理解，可以为imu预积分理论提供非常好的参考意义。另外，本文不是翻译论文，觉得纯翻译没有意义，所以某些地方就用个人理解来表达。言归正传，正式开始解析。（注：该文章参考了很多ORB-SLAM2的技巧，感觉像个非常精简版的ORB-SLAM2）

第一部分：基础知识以及定义

A.坐标系和基本定义

图中定义的也比较清楚，L1, L2....表示的应该是世界坐标系下路标点的位置，论文中没说，但是从公式

可看出，其中cl为摄像机坐标系下的坐标，方便算重投影误差吧。分别表示在Body坐标系下的旋转平移在世界坐标系world下的表示，即B到W，再通俗点就是当前body在world下的位姿。表示向量对应的SE2位姿， 即

代表了3维向量的成员。表示旋转向量与旋转矩阵的转换，即李群对应的李代数。逆变换如下：由于我们主要关注的是Body系关于world系下的表示，因此直接简写为如下形式：

B. 非线性图优化

最小化代价函数如下：

X中的元素代表了图节点和边，ek(x)表示误差函数，为信息矩阵（协方差矩阵的逆），可以简单理解为误差函数的权重。线性化增量方程，代价函数（非线性）可近似为：

ek的雅克比为

可参考视觉SLAM十四讲，将状态变量，雅克比，误差函数构造高斯牛顿增量方程（根据选取的优化方法不同，形式略微差别）

因此更新状态直到收敛，其中

第二部分：SE2-XYZ 约束的图优化

该部分的讲解，还是按照论文中的方式，关于前端跟踪，关键帧的插入，后端关键帧剔除，窗口优化以及回环检测，Global Ba等放入下一篇代码篇进行详细解析。另外论文中，提示为保证实时性以及过滤地面不平，剧烈运动等情况，所以只对关键帧做优化， 下一讲代码中可以看到，前端没有任何优化的部分。位姿图优化如下所示：

A.基于特征的SE2约束

考虑关键帧i，观测到了某个路标点l，测量模型可以写为

 其中表示body和camera之间的旋转和平移，通过提前标定获得（已知量）。代表特征测量噪声服从高斯分布，该噪声项在orb-slam2中根据金字塔层数不同取为n个1.2 相乘，表示的含义也很清楚明白，就是当前检测到的特征点根据图像分辨率不同，大小不同，例如在第0层的时候，不确定为1.2，也就是说，以当前像素为圆心，1.2为半径画个圆，真正的特征可能落在该圆内任意位置，好吧，没有画图，详细大家都能理解，说的不对的地方，请大家指正。再来细看下，公式（7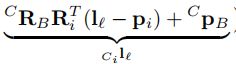），表示的是camera系下，该路标点的3D坐标，表示的是投影矩阵，将camera坐标系转换到像素坐标。论文中指出的具体公式

 的SE2表示

这个公式表示非常简单，不展开了

（fx, fy）表示焦距，（cx, cy）表示主点。

投影矩阵的雅可比很简单，将（9）式展开直接关于路标点求就好了，直接给出论文中的结论 

现在可以合并扰动噪声项到公式（7）假设纵向平移噪声为，旋转噪声扰动为

因此，扰动位姿为

测量模型（7）变为

使用一阶近似，线性化噪声项，u关于​​​​的雅可比如下：

（13）式的雅可比推导也比较简单，先看第一个式子，接下来的推导中，开口向下的尖表示反对称矩阵

开口向上的尖，表示向量

再来看式（13）第二个式子：同上

导数知道了，接下来就是协方差矩阵的传播了，这个传播的推导以后再说吧，这里直接给出论文中的结果。记0均值的噪声项为

 因此，协方差矩阵为

其中是相互独立的，ei是3x3的单位矩阵I3中第i列.

由检测到的特征，与预测特征之间构建SE2-XYZ约束残差

信息矩阵为协方差的逆，关于的雅可比矩阵如下：

如果在省略掉,，则​​​​​统一写为

式（16）的几个雅可比均不需要推导，前两个多出来的部分是因为二维的位姿，省略无关项而已，最后一个推导可参考（13）-2

B. 预积分里程计约束

此处里程计不区分运动学模型，无论差分还是全向模型均可适用，提供k和k+1两个连续帧之间的里程计测量

且SE2上的状态传播

注意传播的依赖于旋转状态为了产生不依赖的两个关键帧i,j之间的测量模块，在(18)式关于rk的那个方程左右同时乘以

因此，关键帧i和j之间的预积分测量和噪声项可表示为：

为了传播积分的噪声项，其迭代过程如下所示：

将（21）写为更紧凑的形式

因此，两时刻的噪声协方差传播公式如下所示：

初始时刻设置为0

此时，两个关键帧之间的里程计约束残差项定义为：

值得说明的是，上式中计算带~的为估计值，不带的为测量值，即假设i时刻轮式里程计输出的结果为(x，y, theta)，估计值应该为（x * uncertain + noise , y * uncertain + noise, theta * uncertain + noise）,这里理解的可能有问题，作为开放问题讨论下吧。

根据式（19）-（23）残差的信息矩阵为，雅克比矩阵求解如下：

这个雅可比推导很简单，再来推导下，（25）中第一个式子的倒数为分别对式（24）残差项中的状态量求雅可比，即

先对i时刻状态求雅可比

至此，论文中的关于雅可比的导数均已推导，目前可能还存在编辑上的错误，请大家谅解，打字编辑公式不容易啊，好了，希望对大家有所帮助吧