高频电阻电容电感

---

---

目录

高频电阻

高频电容

高频电感

---

高频电阻

在低频电子学中，最普通的电路元件是电阻,它的用途是通过将一些电能转换成热产生电压降。现在存在的几种类型的电阻：

高密度介质小颗粒的碳素电阻

采用镍或其他柔性金属丝的线绕电阻

温度稳定材料的的金属膜电阻

采用铝或铍基材料的薄膜贴片式电阻

目前在射频和微波电路中应用的主要是薄膜贴片式电阻。

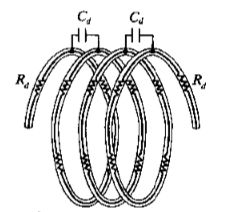
在高频电路下即使是一根直导线也具有电感。而标称值为R的高频电阻的等效电路模型比较复杂，必须根据其引线长度和寄生电容进行修正。

高频电阻等效电路模型

 

在上图中，两个电感L模拟引线，电容用于等效实际的引线布局；电容用于模拟电荷分离效应；用于模拟内部引线电容。相对于标称电阻R，引线电阻常常被忽略。内部引线电阻通常小于线圈的寄生电容，在许多情况下完全可以忽略。

对于线绕电阻，其模型更加复杂，除了引线电感和接触电容，必须引入电阻线圈的电感,以及线圈的寄生电容,而内部引线电容通常被忽略。

高频线绕电阻等效电路模型

例：长2.5cm，AWG26铜线(半径0.2032mm)连接的2K金属薄膜电阻的高频阻抗特性，其中寄生电容为5pF，铜的电导率。

直导线高频近似电感

                                                                

其中(单根导线长度)，对应于两条引线。该是只适用于高频，即。

整个电路的阻抗：

                                                                     

---

高频电容

当平板的尺度大于其间隔时，常规电路分析理论对平行板电容器的电容定义如下：

                                                                             

其中A是平行板的表面积，d代表平行板的间隔。理想情况下，平板间没有电流。然而，在高频时，电介质变得似乎有损耗了。所以电阻器的阻抗必须表示成电导和电纳的并联组合:

                                                                             

在这个表达式中，直流电起源于电导,其中是介质的电导率。目前习惯与引入损耗角正切(loss tangent),带入表达式得

                                                          

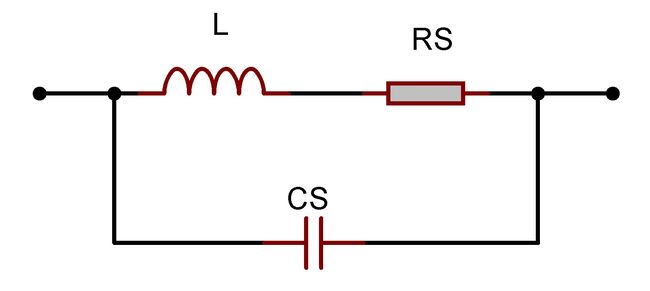
考虑到寄生引线电感L、对于引线欧姆损耗的串联电阻,以及介质损耗电阻的等效电路如图

高频电容的等效电路

例：计算一个47pF电容器的高频阻抗，电容器的电介质为,其损耗角正切为(假定与频率无关)。电容引线是AWG26铜线，长1.25cm。

引线电感

                                                              

其中，对应于两条引线。

引线串联电阻

                                                 

                                                        

泄露电阻

                                                        

则等效电容阻抗

                                                                 

计算旁路电容时假设，假设损耗角正切与频率无关。事实上这个系数与工作频率密切相关。通常情况下手册中的损耗角正切只适用于低频，该数值不能正确反映其射频性能。

损耗角正切也能定义为等效串联电阻(equaivalent series resistance,ESR)与电容的电抗之比，因此很多技术手册上给出的是等效串联电阻，其值由下面公式确定

                                                                                    

电容量与温度也有关，其特性可定量表示为

                                                                           

其中，是标称的电容量，是温度系数，可正可负。

---

高频电感

高频电路中，电感的等效模型如下图，并联寄生电容和串联电阻分别代表电容和电阻的综合效应。

电感线圈中的分布电容和串联电阻

高频电感器的等效电路

例：已知射频扼流圈(电感)直径为1.27mm(空气芯)，N=3.5匝，由AWG36铜线绕成，假设线圈的长度是1.27mm，并联寄生电容约为0.3pF。求射频扼流圈的射频响应。

空气芯线圈电感器结构尺寸示意图

当时，可以采用下面的公式估算电感

                                                                               

但这里不满足，采用下面公式估算电感

                                                                                

 

得

根据导线支流电阻，在忽略趋肤效应的条件下，计算串联电阻

                                                               

射频扼流圈的频率响应如图

假如串联电阻为零，那么谐振是的总阻抗将趋于无穷大，但是由于不为零，所以总阻抗最大值是有限的。通常采用品质因数Q描述线圈串联电阻的影响。

                                                                                     

其中,X是电抗，是线圈的串联电阻。这个品质因数的定义只有对纯粹的集中参数元件电路才是精确的。