一般迭代法（二）| 迭代法的收敛速度（收敛阶）+收敛过程的加速（Aitken加速法）

1. 迭代法的收敛速度

迭代过程的收敛速度，是指迭代误差的下降速度。迭代法的收敛速度一般用收敛阶来描述。

定义2：对于收敛的迭代法$x_{k+1}=\phi (x_k),(k=1,2,\cdots )$，如果存在常数$p\ge 1,c>0$，使得
$$li{m}_{k\to \infty }\frac{e_{k+1}}{e_k^p}=C$$
成立（其中$e_k=|x_k-x^{\ast }|$），则称该迭代法时p阶（次）收敛的。特别地，当$p=1$时称为线性收敛，$p=2$时称为平方收敛。

例2：讨论一般迭代法$x_{k+1}=\phi (x_k),(k=1,2,\cdots )$的收敛速度。

解：令$x^{\ast }=\phi (x^{\ast })$，所以$x_{k+1}-x^{\ast }=\phi (x_k)-\phi (x^{\ast })$。根据中值定理，有
$$x_{k+1}-x^{\ast }=\phi (x_k)-\phi (x^{\ast })={\phi }^{\prime }(\xi )(x_k-x^{\ast })$$
$\xi$为$x_k$与$x^{\ast }$之间的某一点。

因为$e_{k+1}=x_{x+1}-x^{\ast },e_k=x_k-x^{\ast }$，所以当$x_k$在根$x^{\ast }$附近时，有$e_{k+1}={\phi }^{\prime }(x^{\ast })e_k$。

可见，当$\phi (x^{\ast })\ne 0$时，一般迭代法$x_{k+1}=\phi (x_k),(k=1,2,\cdots )$，具有线性收敛性。

定理3：对于迭代过程$x_{k+1}=\phi (x_k)$，如果迭代函数$\phi (x)$在所求根$x^{\ast }$的邻近有连续二阶导数，且$|{\phi }^{\prime }(x^{\ast })<1|$，则有：

（1）当${\phi }^{\prime }(x^{\ast })\ne 0$时，迭代过程为线性收敛；

（2）当${\phi }^{\prime }(x^{\ast })=0$，而${\phi }^{\prime \prime }(x^{\ast })\ne 0$时，迭代过程为平方收敛。

一般迭代法的收敛速度还可以是p阶收敛的。设$\phi (x)$在$x=\phi (x)$的根$x^{\ast }$附近有连续的p阶导数，且${\phi }^{\prime }(x^{\ast })={\phi }^{\prime \prime }(x^{\ast })=\cdots ={\phi }^{(p-1)}(x^{\ast })=0,{\phi }^{(p)}(x^{\ast })\ne 0$，则迭代过程$x_{k+1}=\phi (x_k)$是p阶收敛的。

在用迭代法求解方程的根时，可以先判断迭代函数的收敛速度，然后再具体计算。

2. 收敛过程的加速

一个收敛的迭代过程，只要迭代次数足够多，就可以使计算结果达到任意指定的精度。但是，如果收敛过程过于缓慢、计算工作量过大，则在实际计算过程往往要考虑加速收敛过程的问题。

1. 迭代公式的改进

设${\hat{x}}_{k+1}$表示由$x_k$经过一次迭代后所得到的结果${\hat{x}}_{k+1}=\phi (x_k)$，有微分中值定理，有
$$x^{\ast }-{\hat{x}}_{k+1}=\phi (x^{\ast })-\phi (x_k)={\phi }^{\prime }(\xi )(x^{\ast }-x_k)$$
其中，$\xi$为$x_k$与$x^{\ast }$之间的某一点。假设${\xi }^{\prime }(x)$在求根范围内变化不大，可以近似地看成某个定值q，根据迭代法的收敛条件，有$|q|<1$。于是有：
$$x^{\ast }-{\hat{x}}_{k+1}\approx q(x^{\ast }-x_k)$$
从而
$$x^{\ast }\approx \frac{1}{1-q}{\hat{x}}_{k+1}-\frac{q}{1-q}{x}_k$$
故
$$x_{k+1}={\hat{x}}_{k+1}+(x^{\ast }-{\hat{x}}_{k+1})=\frac{1}{1-q}{\hat{x}}_{k+1}-\frac{q}{1-q}{x}_k\text{\hspace{1em}(3)}$$
$x_{k+1}$比${\hat{x}}_{k+1}$更接近根$x^{\ast }$。因此，迭代收敛的过程得到了加速。

构造一般迭代法加速公式的具体方法如下：

（1）${\hat{x}}_{k+1}=\phi (x_k)$；

（2）$x_{k+1}={\hat{x}}_{k+1}+\frac{q}{1-q}({\hat{x}}_{k+1}-x_k)$，其中$|q|<1$。

2. Aitken（埃特金）加速法

在公式（3）中确定q时，需要计算迭代函数的导数${\phi }^{\prime }(x)$。这在实际计算中是不太方便的，因此可以作进一步改进。由于在上面已有：
$${\hat{x}}_{k+1}=\phi (x_k),x^{\ast }-{\hat{x}}_{k+1}=q(x^{\ast }-x_k)$$
故将迭代值${\hat{x}}_{k+1}$再进行一次迭代计算，得：
$${\overline{x}}_{k+1}=\phi ({\hat{x}}_{k+1}),x^{\ast }-{\overline{x}}_{k+1}=q(x^{\ast }-{\hat{x}}_{k+1})$$
所以
$$\frac{x^{\ast }-{\hat{x}}_{k+1}}{x^{\ast }-{\overline{x}}_{k+1}}=\frac{(x^{\ast }-x_k)}{(x^{\ast }-{\hat{x}}_{k+1})}$$
解得
$$x^{\ast }\approx {\overline{x}}_{k+1}-\frac{({\overline{x}}_{k+1}-{\hat{x}}_{k+1}{)}^2}{{\hat{x}}_{k+1}-2{\hat{x}}_{k+1}+x_k}$$
于是，就有如下迭代公式：
$$(1){\hat{x}}_{k+1}=\phi (x_k)(2){\overline{x}}_{k+1}=\phi ({\hat{x}}_{k+1})(3)x_{k+1}={\overline{x}}_{k+1}-\frac{({\overline{x}}_{k+1}-{\hat{x}}_{k+1}{)}^2}{{\hat{x}}_{k+1}-2{\hat{x}}_{k+1}+x_k}$$
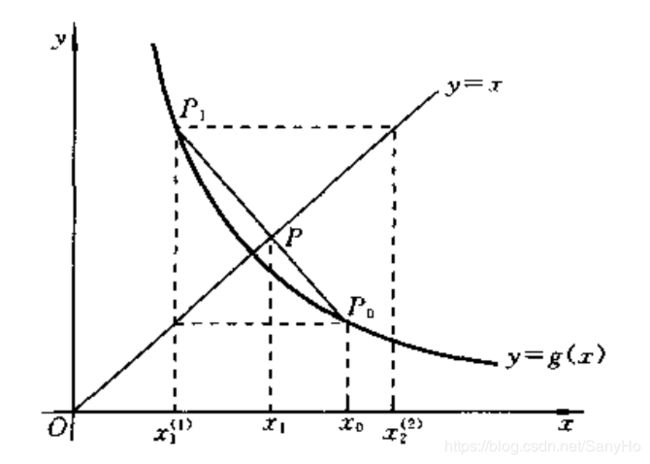
Aitken加速法的几何解释如下图所示。假设$x_0$为方程$x=g(x)$的一个近似根，由$x_1^{(1)}=g(x_0)$和$x_1^{(2)}=g(x_1^{(1)})$，在曲线上$y=g(x)$上可以定出两点$p_0(x_0,x_1^{(1)})$和$p_1(x_1^{(1)},x_1^{(2)})$，作弦线$\overline{p_0{p}_1}$与直线$y=x$交于p。则p点坐标$x_1$满足：
$$x_1=x_1^{(1)}+\frac{x_1^{(2)}-x_1^{(1)}}{x_1^{(1)}-x_0}(x_1-x_1^{(1)})$$
解出$x_1$，即得Aitken加速公式。