《Digital Integrated Circuit》读后笔记 (三)

本文仅为个人娱乐分享，请勿用作其他用途

chapter six Static CMOS Design

1. combinational logic

sequential logic a combinational logic portion and a module that holds the state

2. Static CMOS Design

static complementary CMOS output is either $V_{DD}$ or $V_{SS}$ through a low-resistance path.

dynamic circuit class relies on temporary storage of signal values on the capacitance of high-impedance circuit nodes. simpler and faster sensitive to noise

• complementary CMOS
• ratioed logic(pseudo-NMOS and DCVSL)
• pass-transistor logic

3. Complementary CMOS

pull-up network PUN PMOS

pull-down network PDN NMOS

series devices and parallel devices duality principle

N-input logic gate is 2N

sub-nets(SN)

---

Static properties: (Noise Margin)

• A=B=0->1: a strong pull-up
• A=1, B=0->1: $V_{Tn1}=V_{tn0}$
• A=0->1, B=0: $V_{Tn2}=V_{tn0}+\gamma ((\sqrt{|2{\varphi }_T+V_{int}|}-\sqrt{2{\varphi }_T}))$

---

Propagation Delay:

depends upon the input patterns

$t_{pLH}=0.69R_p{C}_L$

$t_{pHL}=0.69(2R_N{C}_L)$

To make the same delay, NMOS devices must be made twice as wide. PMOS remain unchanged.

High-to-low propagation delay depends on the state of the internal nodes.

PMOS devices have a lower mobility relative to NMOS devices, stacking devices in series must be avoided as much as possible.

NAND is better than NOR.

---

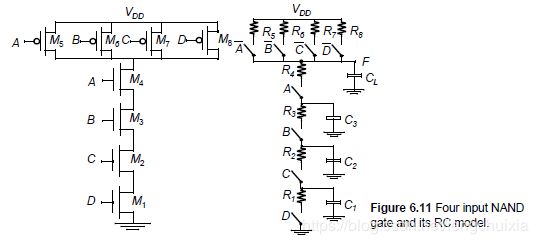
$$t_{pHL}=0.69(R_1{C}_1+(R_1+R_2)C_2+(R_1+R_2+R_3)C_3+(R_1+R_2+R_3+R_4)C_L)$$

$$=0.69R_N(C_1+2C_2+3C_3+4C_L)$$

---

Conclusion:

• Significant implementation area. 2N gate
• propagation delay is a function of the fan-in.
• $t_p=a_{1}FI+a_{2}F{I}^2+a_{3}FO$

---

Solution:

• Transistor Sizing be used with caution

• Progressive Transistor Sizing：$M_1>M_2>M_3>M_4$ not simple in a real layout

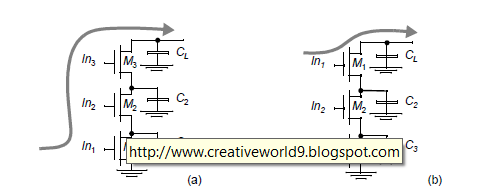
• Input Re-Ordering: critical path

  

• Logic Restructuring

---

$t_p=t_{p0}(1+\frac{C_{ext}}{\gamma C_g})=t_{p0}(1+f/\gamma )$

Modify: $t_p=t_{p0}(p+gf/\gamma )$

$f$ :electrical effort

$p$: the ratio of the intrinstic delays of the complex gate and the simple inverter

$g$: logic effort

$h$: gate effort

Make $t_p$ minimal: $f_1{g}_1=f_2{g}_2=f_3{g}_3=...=f_N{g}_N$

$F=f_1{f}_2{f}_3{f}_4..f_N=C_L/C_{g1}$ $G=g_1{g}_2...g_N$ $H=FG$

$h=\sqrt[N]{FG}=\sqrt[N]{H}$

---

Power Consumption:

dynamic power dissipation: ${\alpha }_{0->1}{C}_L{V}_{DD}^{2}f$ switching activity

Logic function: ${\alpha }_{0->1}=p_0{p}_1=p_0(1-p_0)$

Assuming the inputs are independent and uniformly distributed

${\alpha }_{0->1}=\frac{N_0}{2^N}\frac{N_1}{2^N}$

• a conditional probability
• glitches/dynamic hazards long chains of gates

Solutions: To reduce the switching factor

• Logic Restructuring

  • Chain structure
  • Tree structure

• Input ordering

  postpone the introduction of signals with a high transition rate

• Time-multiplexing resources

  can minimize the implementation area. Very few transitions

• Glitch Reduction by balancing signal paths

  Make every gate change simultaneously Redesigning the network

4. Ratioed Logic

reduce robustness and extra power dissipation reduce number of gates $N+1$

pseudo-NMOS gate nominal low output is not 0V

ratioed: voltage swing on the output and the overall functionality of the gate depends upon the ratio between the NMOS and PMOS sizes.

$V_{OL}\approx \frac{{\mu }_p{W}_p}{{\mu }_n{W}_n}|V_{DSAT}|$ To make $V_{OL}$ smaller, PMOS needs to be sized much smaller, however, it is bad to propagation delay.

static power: $P_{low}=V_{DD}{I}_{low}$

---

differential logic and positive feedback:

DCVSL differetial cascode voltage switch logic

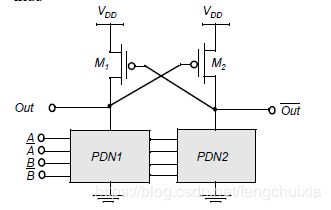
have rail-to-rail swing static power dissipation is eliminated

Of course, short circuit path still exists.

5. Pass-transistor logic

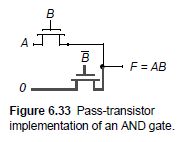
Reduced number of devices low capacitance

high output is $V_{DD}-V_{Tn}$ low switching energy

pass-transistor gates cannot be cascaded by connecting the output of a pass gate to the gate input of another pass transistor.

may cosume static power when the output is high. insufficient to turn off the PMOS transistor of CMOS

---

Differential Pass Transistor Logic:

CPL DPL

• complex gates such as XORs can be realized with a small number of transistors
• CPL is static gates

---

Solutions:

• Level restoration:

  level restorer

  

can eliminates any static power dissipation in the inverter.

the resistance of $M_n$ and $M_r$ must be such that the voltage at node $X$ drops below the threshold of the inverter.

The rise time of the gate is further negatively affected, since, the level-restoring transistor $M_r$ fights the decrease in voltage at node $X$

---

swing-restored pass transistor logic

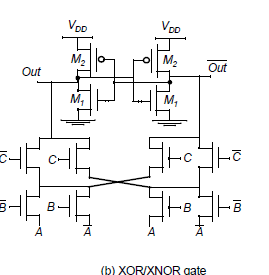
• Multiple-threshold transistors:

  zero-threshold transistor can make the subthreshold currents

• Transmission gate logic:

  

NMOS devices pass a strong 0 but a weak 1, while PMOS transistor pass a strong 1 but a weak 0.

rail-to-rail swing

can realize multiplexer and XOR gate using less transistors.

$R_{eq}$ is relatively constant.

---

$t_p=0.69\sum _{k=0}^{n}C{R}_{eq}k=0.69C{R}_{eq}\frac{n(n+1)}{2}$

solution:

break the chain and insert buffers every $n$ switches.

$t_p=0.69[\frac{n}{m}C{R}_{eq}\frac{m(m+1)}{2}]+(\frac{n}{m}-1)t_{buf}$

$m_{opt}=1.7\sqrt{\frac{t_{pbuf}}{C{R}_{eq}}}\approx 3$

6. Dynamic CMOS Design

to avoid the static power dissipation

precharge and evaluation phases determined by the signal $CLK$.

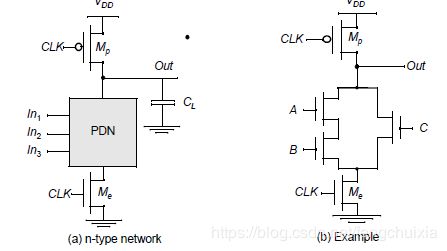
$CLK=1$: evaluation phase

$CLK=0$: precharge phase

During evaluation phase, the output can make at most one transition.

• number of transistors: $N+2$ numbers

• non-ratioed

• only consumes dynamic power

• faster switching speeds

---

Speed and Power dissipation of dynamic logic

• $t_{pLH}=0$
• no glitches only one transition
• a higher switching activity: ${\alpha }_{0->1}=p_0$

---

Problems:

• charge leakage:

Source 1 and 2: reverse-biased diode and sub-threshold leakage

require a minimal clock rate

solution: adding a bleeder transistor

• charge sharing:

  share capacitor $C_L$ and $C_a$

  we need to keep the value of $\Delta V_{out}$ below $|V_{tp}|$

  solution:

  precharge critical internal nodes

• Capacitive coupling：

  back-gate coupling

  example: a dynamic two-input NAND gate drives a static NAND gate

• clock-feedthrough:

  causes the output of the dynamic node to rise above $V_{DD}$ on the low-to-high transition of the clock.

  may cause forward-biased.

Cascading Dynamic gates:

the inputs can only make a single 0->1 transition during the evaluation period.

---

Domino Logic:

consist of an n-type dynamic logic block followed by a static inverter.

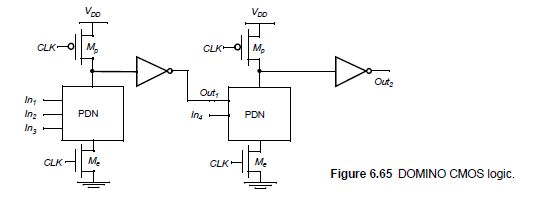
• pure Domino design has become rare.

• high speed only a rising edge delay exists.

Dual-rail Domino

$np$-CMOS