LeetCode 115. 不同的子序列 从暴力递归到动态规划，从动态规划到优化

在 LeetCode 上刷题刷到了一道 Hard 的题 115. 不同的子序列 ，用暴力递归的话，逻辑其实很好写，就是复杂度太高，测试用例复杂一些就直接GG，我就采用了牛客左程云左神的思想，将暴力递归改成动态规划，并通过评论区大神的思路将正向的动态规划进行优化变成逆向的动态规划。记录一下，进一步加深对动态规划的理解。

-------------------------------------------------------------------------------------------------------------------------------------------------------------

题目描述

115. 不同的子序列

给定一个字符串 S 和一个字符串 T，计算在 S 的子序列中 T 出现的个数。
一个字符串的一个子序列是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。
（例如，"ACE" 是 "ABCDE" 的一个子序列，而 "AEC" 不是）

示例 1:   输入: S = "rabbbit", T = "rabbit"     输出: 3
解释:  有 3 种可以从 S 中得到 "rabbit" 的方案。

示例 2:   输入: S = "babgbag", T = "bag"    输出: 5
解释:  有 5 种可以从 S 中得到 "bag" 的方案。

--------------------------------------------------------------------------------------------------------------------------------------------------------------

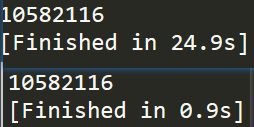
这一题，我的第一想法就是暴力递归，代码如下。通过记录当前走到的下标 i 和 j 来判断是否相等，若 s[ j ] == t[ i ]， 则可以将 目标字符串的下标加一然后继续匹配（即选中当前字符）。其中，无论 s[ j ] 是否等于 t[ i ] 都需要不选择当前字符，然后继续进行递归。递归的终止条件为字符串  s 或  t  的下标走到最后的位置，当字符串 t 走到最终位置时，发生了一次匹配， res++ 。代码比较简单，测试用例一下过，提交完直接超时，最后的测试用例为 "aabdbaabeeadcbbdedacbbeecbabebaeeecaeabaedadcbdbcdaabebdadbbaeabdadeaabbabbecebbebcaddaacccebeaeedababedeacdeaaaeeaecbe"   "bddabdcae"  结果应该为 10582116。 在我本地的运行时间为 24.9s ，太慢了，暴力递归虽简单，时间复杂度也是相当高的。

class Solution {
public:
    int numDistinct(string s, string t) {
        int res = 0;
        dfs(res, s, t, 0, 0);
        return res;
    }
    void dfs(int& res, string s, string t, int i, int j){
        if(i==t.size()){
            res++;
            return ;
        }
        if(j==s.size()) return ;
        // 是否相等都要走这一步
        dfs(res, s, t, i, j+1);
        // 发生匹配时，字符串 t 的下标 +1 然后进行匹配
        if(s[j]==t[i]) dfs(res, s, t, i+1, j+1);
    }
};

于是，我根据暴力递归的版本改出了一个基本的动态规划，根据暴力递归的下标值的范围可以确定dp矩阵的范围，从0到字符串的长度，即需要一个  dp[ t.size()+1 ] [ s.size()+1 ]  的矩阵。其中，dp[ i ][ j ] 代表当字符串 s 走到 j 位置，字符串 t 走到 i 位置， 有多少次匹配。其中暴力递归中  dfs(res, s, t, i, j+1)  对应  dp[ i ][ j ] = dp[ i ][ j+1 ]， dfs(res, s, t, i+1, j+1)  对应  dp[ i ][ j ] = dp[ i+1 ][ j+1 ]。 初始化第一行的意义是字符串 s 匹配空字符串的结果， 结果为 1 。

S = "babgbag", T = "bag" 时的 dp矩阵

*    *    b    a    b    g    b    a    g

*    0    1    1    1    1    1    1    1

b    0    1    1    2    2    3    3    3

a    0    0    1    1    1    1    4    4

g    0    0    0    0    1    1    1    5

class Solution {
public:
    int numDistinct(string s, string t){
        vector> dp(t.size()+1, vector(s.size()+1, 0));
        // 初始化最后一行，相当于 匹配空字符串
        for(int j=0; j<=s.size(); ++j) dp[t.size()][j] = 1;
        for(int i=t.size()-1; i>=0; i--)
            for(int j=s.size()-1; j>=0; j--){
                // 是否相等都要加上前面的值
                dp[i][j] = dp[i][j+1];
                // 相等时加上，上一个字符匹配得出的结果
                if(s[j] == t[i]) dp[i][j] += dp[i+1][j+1];
            }
        return dp[0][0];
    }
};

优化的动态规划，首先，再空间复杂度上，可以把解法从 O（M×N）优化为 O(N) ，N 为字符串 s  的长度，代码如下,

class Solution {
public:
    // 降低空间复杂度的动态规划
    int numDistinct(string s, string t){
        // 初始化第一行
        vector dp(s.size()+1, 1);
        // 记录上一个保存的值
        int pre = 1;
        for(int i=1; i<=t.size(); ++i)
            for(int j=0; j<=s.size(); ++j){
                int tem = dp[j];
                if(j==0) dp[j] = 0;
                else {
                    // 是否相等都要加上前面的值
                    dp[j] = dp[j-1];
                    // 相等时加上，上一个字符匹配得出的结果
                    if(s[j-1] == t[i-1]) dp[j] += pre;
                }
                pre = tem;
            }

        return dp[s.size()];
    }
};

进一步优化，列主序，把空间复杂度优化为 O（M），M 为字符串 t 的长度，代码如下：

其中， dp [ i ] 代表字符串 s 匹配到  字符串 t  从 0 到下标 i 的结果个数

当S = "babgbag", T = "bag"  dp矩阵的变化情况为
b: 1 1 0 0  -->  a: 1 1 1 0  -->  b: 1 2 1 0 --> g: 1 2 1 1
b: 1 3 1 1  -->  a: 1 3 4 1  -->  g: 1 3 4 5

class Solution {
public:
    // 倒序计算，不用保存pre
    // 列主序，进一步降低空间复杂度的动态规划
    int numDistinct(string s, string t){
        // 初始化第一行
        vector dp(t.size()+1, 0);
        // 代表当字符串 s 匹配空字符串时的结果
        dp[0] = 1;
        for(int i=0; i=0; --j)
                if(s[i] == t[j]) dp[j+1] += dp[j];

        return dp[t.size()];
    }
}

进一步优化，列主序，对字符串 t 构造字典，优化时间复杂度， 代码如下：

当S = "babgbag", T = "baga" 时
next数组为 -1  -1  -1  1    hash[a] = 3   hash[b] = 0   hash[g] = 2 
dp矩阵的变化情况为
b: 1 1 0 0 0 -->  a: 1 1 1 0 0 -->  b: 1 2 1 0 0 --> g: 1 2 1 1 0
b: 1 3 1 1 0 -->  a: 1 3 4 1 1 -->  g: 1 3 4 5 1

class Solution {
public:
    // 列主序，通过构造 t 的字典，进一步降低时间复杂度的动态规划
    // 倒序计算，不用保存pre
    int numDistinct(string s, string t){
        // 初始化第一行
        vector dp(t.size()+1, 0);
        // 代表当字符串 s 匹配空字符串时的结果
        dp[0] = 1;

        // 构造 t 的字典，当字符串的字符重复时，通过 next 数组访问下一个
        vector hash(128, -1);
        vector next(t.size(), -1);
        for(int i=0; i=0; j = next[j])
                dp[j+1] += dp[j];

        return dp[t.size()];
    }
};

最后贴一张暴力递归和动态规划的时间对比