SOM神经网络、LVQ神经网络、CPN神经网络与Python实现

竞争型学习神经网络

简述

最近对神经网络比较感兴趣，因此花了两三天时间对整个领域进行了简单的调研，梳理和学习。其中深度学习，尤其以我们熟悉的如今大火的深度网络模型,如CNN, RNN, GAN和AE及它们的子类等；是在本世纪初，硬件性能达到了一个新的高度后才能有如此巨大的发展的。事实上在21世纪之前，各种各样的神经网络模型已经被发明并应用。那时候由于硬件性能的限制，以及由通信网络不发达导致的数据量匮乏，并没有人敢去思考如何用巨大的算力去挖掘大数据。那时的网络一般是借助设计网络结构的技巧取胜(比如很多网络不借助编程，而是直接用硬件实现)，其中很多网络在今天，其设计理念也是值得借鉴的。
为此，我在两三天的时间里，学习了一些从上世纪60年代，到本世纪初出现的一些经典的神经网络模型，并在此整理并给出代码。

竞争层

我们本篇主要介绍竞争型的神经网络，即在网络中出现竞争层的网络。竞争层比起我们熟悉的全连接层要朴素很多；
首先，竞争层会接受一个向量样本，每个竞争层中的神经元都自带一个和该样本维度相同的向量，称作"权向量"。然后，用每个权向量和输入向量按照一定规则进行比较，相似程度最高的那个称作获胜神经元。
然后在输出时，只有获胜神经元会输出1，其他神经元输出0，也就是胜者通吃的法则。这一特点也就决定了，在使用反向传播算法训练这种网络时，只有获胜神经元会受到训练。
讲到这里大家可能会发现，这种训练方法有点类似聚类中的K-means算法。通过比较中心向量和样本的相似程度，调整中心向量。的确，两者理念是相同的。而这一特点也就决定了竞争型网络既可以用于监督学习，也可以用于无监督学习。

SOM神经网络简述

首先，我们来介绍Self-Organizing feature Map，自组织特征映射网络，som是一种自组织的网络结构，常用于数据的聚类和降维。网络的结构非常简单，只有一层竞争层，接受输入向量并进行比较后，直接输出结果。

其主要特点是网络内部的拓扑结构，为什么它叫"自组织"网络？因为SOM在执行基本的竞争层工作的同时，不止是调整获胜神经元，还会调整获胜神经元附近的神经元。为什么要进行这样的操作呢？我们可以想象，在我们的训练过程中，相似的样本会在向量空间中相对接近，形成一个独立的簇状。如果让相邻的神经元也去靠近同样的样本，则很大概率会让训练出的网络的相邻神经元，在向量空间中也越接近，表征这相同的类别。WIKI上的一张图就很形象。

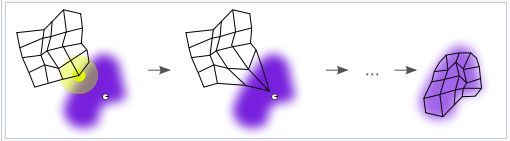
其训练分为：

1. 初始化每个节点的权重。权重设置为标准化小型随机值。
2. 从训练集中随机选择一个向量并呈现给网格。
3. 检查每个节点来计算哪一个的权重最像输入向量。这会让你获得最佳匹配单元（BMU）。我们通过迭代所有节点并计算每个节点的权重与当前输入向量之间的欧几里德距离来计算BMU。权重向量和输入向量最接近的节点则被标记为BMU。
4. 计算BMU邻域的半径。在半径范围内找到的节点则认为处于BMU邻域内。
5. 调整在步骤4中发现的节点的权重，让它们更像输入向量。节点和BMU越近，权重调整的越多。重复步骤2，迭代N次。
   评估相似度可以使用单纯的向量欧拉距离，也可以借助度量学习或者归一化等方法帮助训练。

这种方法是一种聚类方法，而又有不同于聚类的地方；因为网络能自组织地学习特征向量空间中的分布，并把相似的分布烙印在自己的网络拓扑结构上，它同时还具备了特征间聚类和可视化的能力。

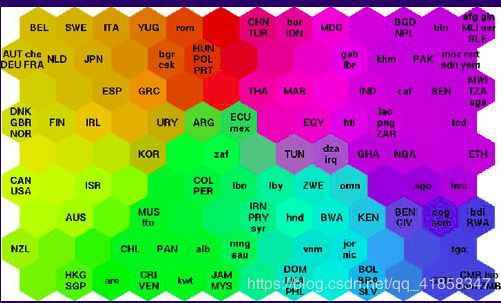
如图，在特征上接近的数据会被聚集在网络拓扑结构相同的区域内。

SOM神经网络实战

TIPS：有关训练的小技巧
第一，SOM和BP网不同，它的学习速度很大程度取决于样本，而不取决于网络当前的学习情况。所以如果想让网络有效训练，一种方法是使用随迭代次数下降的学习率。
第二：在进行自组织训练时，调动周边神经元的一个方法是先计算神经元在网络拓扑上的距离，再根据该距离计算出一个衰减因子。常用的衰减函数有高斯分布、门函数等。
前面说了，SOM网络能用作聚类、降维等工作上。这里我们就分别体验一下它的功能。
考虑这样的一项任务，对一个色彩比较多样的图片，我们想要让它进行简单压缩，让每个像素点的色彩种类限制在几种。即在图片所有像素组成的三维向量空间内寻找到最能表征图片的n种颜色。
这个任务很适合SOM，因为SOM进行的就是向量的竞争，而且最后得到的权值向量就可以直接被用于表征图片的颜色。

首先我们调一下包，常用的numpy和matplotlib等

import numpy as np
import random
from copy import deepcopy
import matplotlib
from matplotlib import pyplot as plt

然后我们设计一个SOM类，以及配套的距离估算函数等。

def gaussian(x, sigma):
    """Returns a Gaussian centered in c."""
    d = (2*np.pi)**0.5*sigma
    return np.exp(-(x**2)/2/(sigma**2))/d

def Manhattan(x1,x2):
    return abs(x1[0]-x2[0])+abs(x1[1]-x2[1])
     

   
class node:
    def __init__(self,input_len,weight):
        self.w = np.ones(input_len)*weight
        self.x = None
        self.y = None
        
    def forward(self, x):
        self.x = x
        vec = (x-self.w).reshape(1,-1)
        self.y = np.dot(vec,vec.T)
        return self.y
    
    def backward(self):
        return (self.x-self.w)
        

class SOM:
    def __init__(self,x,y,input_len,sigma,weight,lr=0.2):
        '''
        输入参数
        x，y：输出层的长宽
        input_len：输入向量的size
        sigma：高斯衰落函数的标准差
        '''
        self.x = x;self.y = y;
        self.nodes = [[node(input_len,weight) for _ in range(y)] for _ in range(x)]
        self.sigma = sigma
        self.lr = lr
        
    def fit(self, data, iter_num=10000):
        for t in range(iter_num):
            lr = self.lr*np.exp(-t/iter_num)
            x = random.choice(data)
            winner = (0,0)
            dist = float("inf")
            for i in range(self.x):
                for j in range(self.y):
                    node = self.nodes[i][j]
                    d = node.forward(x)
                    if d<dist:
                        winner = (i,j)
                        dist = d
            
            i,j = winner
            dw = self.nodes[i][j].backward()
            for m in range(self.x):
                for n in range(self.y):
                    node = self.nodes[m][n]
                    manh = Manhattan((m,n),(i,j))
                    node.w += lr*gaussian(manh,self.sigma)*dw
        
    def predict(self, x):
        res = None
        dist = float("inf")
        for i in range(self.x):
            for j in range(self.y):
                node = self.nodes[i][j]
                d = node.forward(x)
                if d<dist:
                    res = node.w
                    dist = d
        return res
    
    
    def weights(self):
        return [[self.nodes[i][j].w for j in range(self.y)] 
                for i in range(self.x)]

导入一张图片用作训练，这里我用的是我的微信头像’kokoro’

img = plt.imread('kokoro.jpg')
pixels = img.reshape(-1,3).copy()
plt.imshow(pixels.reshape(img.shape))

然后就可以初始化一个网络并且训练了，我们设计的是2*2的矩阵型拓扑结构，可以看到训练后得到的几个权向量如下

som = SOM(2,2,3,0.1,155,0.2)
som.fit(pixels,10000)
som.weights()

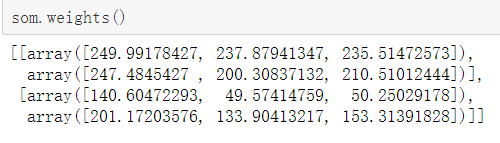
我们把SOM的predict方法用在原图片上，就可以看见被4色化的图片了

zipped = np.zeros(pixels.shape).astype("uint8")
for i in range(len(pixels)):
    x = som.predict(pixels[i])
    zipped[i] = x.astype("uint8")

img_zip = zipped.reshape(img.shape)
plt.subplot(121)
plt.imshow(img_zip)
plt.subplot(122)
plt.imshow(img)

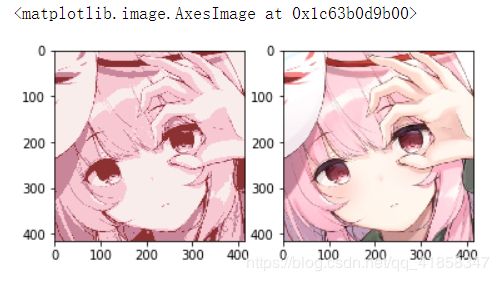
保真度还是相当高的
我们再来体验一下基于SOM的聚类，理论上SOM的聚类效果不应该很好。一是因为它是根据输入向量和权向量间距离直接分类的，效果上肯定比不上高斯混合聚类这种概率模型。二是我这里使用的是简单的欧拉距离，并不能很好的表征一般的特征距离。但我们还是姑且一试

首先导入经典的聚类数据集鸢尾花

from sklearn.datasets import load_iris
iris = load_iris()
descr = iris['DESCR']
data = iris['data']
feature_names = iris['feature_names']
target = iris['target']
target_names = iris['target_names']

初始化网络并训练

som = SOM(2,2,4,0.1,3,0.2)
som.fit(data,10000)
labels = np.zeros(len(data))
dic = {}
cnt = 0
for i in range(len(data)):
    vec = tuple(som.predict(data[i]))
    if not dic.get(vec):
        dic[vec]=cnt
        cnt+=1
    labels[i] = dic[vec]

plt.figure(figsize=(10,4), dpi=80)
plt.subplot(1,2,1)
plt.scatter(data[:,2].reshape(-1), data[:,3].reshape(-1),edgecolors='black',
            c=target)
plt.xlabel('petal length (cm)')
plt.ylabel('petal width (cm)')
plt.title('Iris original distribution')
plt.subplot(1,2,2)
plt.scatter(data[:,2].reshape(-1), data[:,3].reshape(-1),edgecolors='black',
            c=labels)
plt.xlabel('petal length (cm)')
plt.ylabel('petal width (cm)')
plt.title('Distribution by SOM network')

在两个特征上的2Dplot如下，可以看见效果的确一般。

LVQ神经网络简述

下一个，我们来介绍LVQ网络。LVQ学习向量量化算法是一种有监督的聚类算法，目标是在数据分布中找到一组能表征几种数据簇的原型向量。
学习向量量化的算法很简单，就是随机采样一个数据点，并比较该数据点的标签和原型向量自己的标签是否一致。一致则把原型向量向该数据点的方向拉，不一致则把原型向量推走。
网络使用了LVQ的思想，但是在此之上又添加了更多细节。

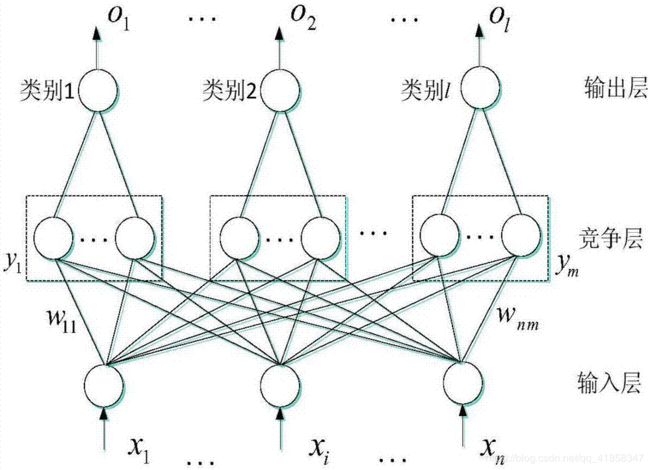
1、使用one-hot的输出形式，每次网络会进行竞争让某个神经元获胜，和同为one-hot的label对比计算误差，如果分类错误就能一次更新两个神经元的权值。
2、对竞争层进行分组，比如竞争层有3M个神经元，而输出层只有M个神经元，每3个神经元以1的连接权重和一个输出层神经元相连接。这样最终结果只有M个分类。尽管整个竞争层只有一个神经元会获胜，但这样的结构保证了一个分类对应的不只是一个向量中心，提高了分类的可靠性。
容易理解的是，网络的思想是很朴素的。就是使用LVQ的思想学习为一个类别学习出几个原型向量，并用这些原型向量分类其他数据。一般来说，它的学习效率和鲁棒性都更好。

LVQ神经网络实战

我们来解决一个纯粹的向量模型分类问题

首先还是先设计一个网络类

class LVQnet:
    def __init__(self, input_sz, output_sz, groups):
        '''
        初始化，给出输入向量的维度和输出的种类数
        groups是竞争层的分组状况，如[1,2,3,2]
        意为竞争层共有8个神经元，4组输出
        '''
        assert len(groups)==output_sz
        self.groups = groups
        self.hidden_sz = sum(groups)
        #随机初始化神经元的原型向量
        self.prototype = np.random.rand(self.hidden_sz,input_sz)*0.01
        self.hidden2out = np.zeros((output_sz,self.hidden_sz))
        cnt = 0
        for i in range(len(groups)):
            for j in range(groups[i]):
                self.hidden2out[i][cnt] = 1
                cnt+=1
        
    def fit(self, X, Y, lr = 0.5, iterations = 1000):
        N = len(X)
        for t in range(iterations):
            gamma = lr*(1-t/iterations)
            idx = random.randint(0,N-1)
            x = X[idx]
            out = self.predict(x)
            y = Y[idx]
            delta = abs(out-y)
            sign = int(np.sum(delta)==0)*2-1
            #根据delta修正获胜神经元的原型向量
            self.prototype[self.winner] += gamma*sign*self.v[self.winner]
    
    def predict(self,x):
        x = np.tile(x,(self.hidden_sz,1))
        v = x-self.prototype
        self.v = v
        distance = np.sum(v**2,axis = 1).reshape(-1)
        winner = np.argmin(distance)
        self.winner = winner
        out = np.zeros((self.hidden_sz,1))
        out[winner][0] = 1
        out = self.hidden2out.dot(out).reshape(-1)
        return out

不需要太多花里胡哨，就是简单的竞争逻辑和原型向量更新规则。
我们把上述的向量丢进网络里训练。

X = np.array(
[
    [-6,0],
    [-4,2],
    [-2,-2],
    [0,1],
    [0,2],
    [0,-2],
    [0,1],
    [2,2],
    [4,-2],
    [6,0]
])
Y = np.array(
[
    [1,0],
    [1,0],
    [1,0],
    [0,1],
    [0,1],
    [0,1],
    [0,1],
    [1,0],
    [1,0],
    [1,0]
])#one-hot形式的编码
network = LVQnet(2,2,[4,2])
network.fit(X,Y,lr = 0.1, iterations=2000)
x = [0 for _ in range(10)]
y = [0 for _ in range(10)]
u = list(X[:,0].reshape(-1))
v = list(X[:,1].reshape(-1))
for i in range(10):
    if np.argmax(Y[i])==0:
        plt.quiver(x[i],y[i],u[i],v[i],color='r',angles='xy', scale_units='xy', scale=1)
    else:
        plt.quiver(x[i],y[i],u[i],v[i],color='g',angles='xy', scale_units='xy', scale=1)

prototype = network.prototype
for i in range(len(prototype)):
    plt.quiver(x[i],y[i],prototype[i][0],prototype[i][1],color='yellow',angles='xy', scale_units='xy', scale=1)
plt.xlim([-6,6])
# Set the y-axis limits
plt.ylim([-6,6])
# Show the plot
plt.show()

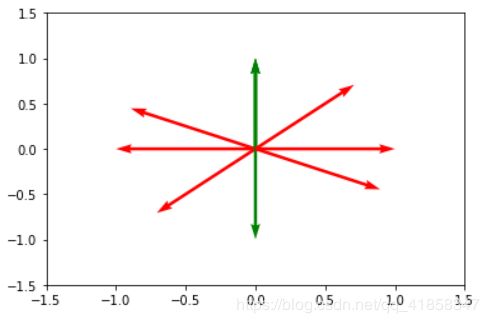
给出的向量样本如图所示

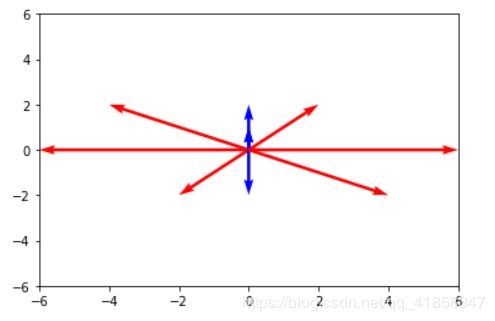
分类得到的原型向量如下图的黄色箭头所示

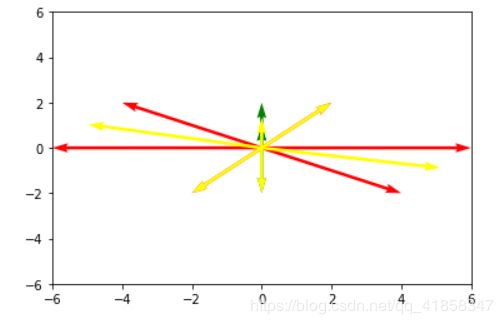
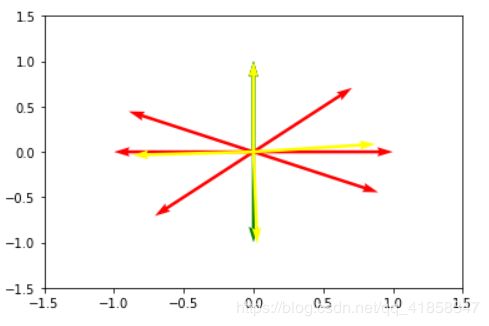
表征两个类需要6个原型向量，如果归一化向量，则可以使用更少。

X = X/np.sqrt((np.tile(np.sum(X**2,axis=1),(2,1)).T))
u = list(X[:,0].reshape(-1))
v = list(X[:,1].reshape(-1))
for i in range(10):
    if np.argmax(Y[i])==0:
        plt.quiver(x[i],y[i],u[i],v[i],color='r',angles='xy', scale_units='xy', scale=1)
    else:
        plt.quiver(x[i],y[i],u[i],v[i],color='g',angles='xy', scale_units='xy', scale=1)
plt.xlim([-1.5,1.5])
# Set the y-axis limits
plt.ylim([-1.5,1.5])
# Show the plot
plt.show()

network = LVQnet(2,2,[2,2])
network.fit(X,Y,lr = 0.1, iterations=2000)

for i in range(10):
    if np.argmax(Y[i])==0:
        plt.quiver(x[i],y[i],u[i],v[i],color='r',angles='xy', scale_units='xy', scale=1)
    else:
        plt.quiver(x[i],y[i],u[i],v[i],color='g',angles='xy', scale_units='xy', scale=1)

prototype = network.prototype
for i in range(len(prototype)):
    plt.quiver(x[i],y[i],prototype[i][0],prototype[i][1],color='yellow',angles='xy', scale_units='xy', scale=1)
plt.xlim([-1.5,1.5])
# Set the y-axis limits
plt.ylim([-1.5,1.5])
# Show the plot
plt.show()

CPN神经网络简述

CPN网络是一种拓扑结构类似三层前馈网络的网络，但是它的训练和使用更为简单。实际上CPN是由一层竞争层和一层全连接层组合而成。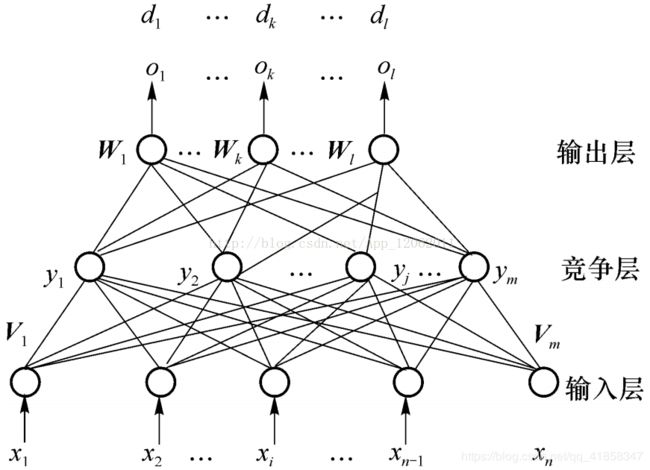
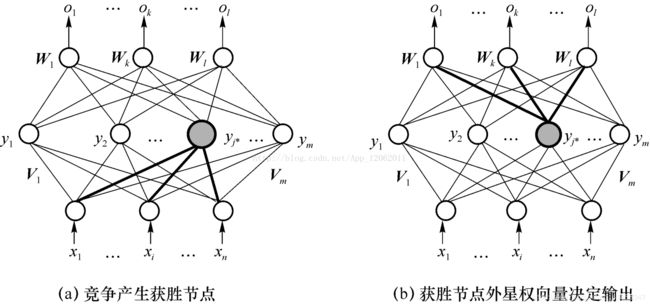
它是一种混合了SOM网络和BP网络的监督聚类方法，首先设置一层竞争层进行简单聚类，这里一般不需要进行自组织。然后再通过全连接层把获胜神经元的y_i=1用权值矩阵传到输出层，并用label反向传播调整权值矩阵。随着算法的演变，权值矩阵将被编码为期望输出的形式。
训练的过程应该不用太多解释，主要是要把训练分为两部分

1. 训练竞争层，让竞争层的权向量收敛到数据分布的聚类中心。训练方法参考上面的SOM的训练，不过一般不用让网络自组织。
2. 训练全连接层，使用简单的反向传播算法。每次输入一个向量后，竞争层有一个神经元被激活，它的输出为1，其他输出为0.这样，整个网络的输出也就是该神经元对应的全连接层的连接权。然后通过对比该连接权和真实输出，确定权向量的正确取值。

竞争层的部分有时需要进行向量的归一化处理。很容易看出，CPN比起SOM就是多做了一个编码的工作。让聚类的无标签形式变成监督情形的有标签形式。
CPN的缺点依然很明显，如果竞争层的聚类效果不好，就有很大概率在进行权值矩阵编码时发生震荡，致使网络不收敛。

CPN神经网络实战

我们来实践一下，解决下面的这个模式分类问题

定义网络

class CPNnet:
    def __init__(self, input_sz, hidden_sz, output_sz):
        '''
        初始化，给出输入向量的维度和输出的种类数
        此外还需要给出隐层数目，也就是中心向量的数目
        '''
        self.values = np.random.rand(hidden_sz,input_sz)
        self.sz = hidden_sz
        self.W = np.zeros((hidden_sz,output_sz))
        
        
    def fit(self, X, Y, lr = 1, iterations = 1000):
        #首先把value向量调整到适应X的情况
        #rand生成的是 [0,1]的均匀分布，计算X各维度的均值并做归一化
        means = np.tile(np.mean(X,axis=0),(self.sz,1))
        self.values *= 2*means
        N = len(X)
        #阶段1，对隐层向量进行训练
        for t in range(iterations):
            gamma = lr*(1-t/iterations)
            idx = random.randint(0,N-1)
            x = X[idx]
            out = self.predict(x)
            self.values[self.winner] += gamma*(x-self.values[self.winner])
        #阶段2，对权值矩阵进行训练
        for t in range(iterations//10):
            gamma = lr*(1-t/iterations)
            idx = random.randint(0,N-1)
            x = X[idx]
            y = Y[idx]
            out = self.predict(x)
            delta = out-y
            self.W[self.winner] -= gamma*delta
    
    def predict(self,x0):
        x = deepcopy(x0)
        minus = self.values-np.tile(x,(len(self.values),1))
        dist = np.sum(minus**2,axis=1).reshape(-1)
        winner = np.argmin(dist)
        self.winner = winner
        out = self.W[winner]
        return out

首先我们来看看网络能否收敛到目标的几个向量上

X0 = np.array([
    [0.0,0.0],
    [0.5,0.0],
    [0.0,0.5],
    [1.0,1.0],
    [0.5,1.0],
    [1.0,0.5]
])
Y0 = np.array([
    [1,0,0,0,0],
    [1,0,0,0,0],
    [0,1,0,0,0],
    [0,0,1,0,0],
    [0,0,0,1,0],
    [0,0,0,0,1]
])
X = deepcopy(X0)
Y = deepcopy(Y0)
cpn = CPNnet(2,6,5)
cpn.fit(X,Y)
for x in X:
    print(cpn.predict(x))

可以看见，网络找到了对应的权向量，而且对它们进行了正确编码。
我们尝试一下预测任务

x = np.array([0.2,1])
print(cpn.predict(x))
x = np.array([1,0.2])
print(cpn.predict(x))
x = np.array([0.7,0.6])
print(cpn.predict(x))

再来尝试一下鸢尾花聚类任务

iris = load_iris()
descr = iris['DESCR']
data = iris['data']
feature_names = iris['feature_names']
target = iris['target']
target_names = iris['target_names']

X = deepcopy(data)
# 把target进行独热编码
Y = np.zeros((len(target),3))
for i in range(len(target)):
    Y[i][target[i]] = 1
cpn = CPNnet(4,10,3)
cpn.fit(X,Y)
labels = [np.argmax(cpn.predict(x)) for x in X]
plt.figure(figsize=(10,4), dpi=80)
plt.subplot(1,2,1)
plt.scatter(data[:,0].reshape(-1), data[:,1].reshape(-1),edgecolors='black',
            c=target)
plt.xlabel('sepal length (cm)')
plt.ylabel('sepal width (cm)')
plt.title('Iris original distribution')
plt.subplot(1,2,2)
plt.scatter(data[:,0].reshape(-1), data[:,1].reshape(-1),edgecolors='black',
            c=labels)
plt.xlabel('sepal length (cm)')
plt.ylabel('sepal width (cm)')
plt.title('Distribution by CPN')

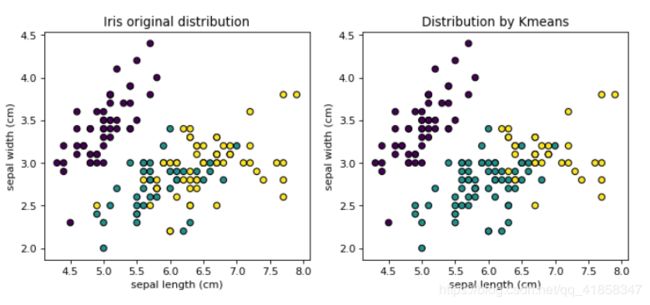
网络为数据打上了正确的标签，但是仍然没能克服竞争层存在的泛化能力差的固有问题。

小结

简单总结下，竞争型网络一般用于聚类和数据降维任务，可以有监督学习，也可以无监督学习。由于竞争层只会激活一个神经元，在训练时也只需要修改该神经元对应的一组权值，因此训练十分高效。但是竞争层也有其固有的缺点，即分类正确率比较低，在有各种强大的非线性分类模型和机器学习算法的当今，把它用于分类任务并不明智。不过这种网络结构在计算资源匮乏的20世纪仍然是具有创造性的。