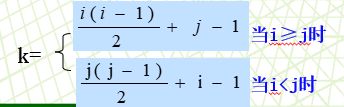数据结构(C语言)第二版 第四章课后答案

数据结构(C语言)第二版 第四章课后答案

1~5 B B C A B
6~10 B B C B B
11~15 A B D (C,B) C

1．选择题

（1）串是一种特殊的线性表，其特殊性体现在（B） 。
A．可以顺序存储 B．数据元素是单个字符
C．可以链式存储 D．数据元素可以是多个字符若

字符串简称串，是一种特殊的线性表，它的数据元素仅由一个字符组成。

（2）串下面关于串的的叙述中，（B）是不正确的。
A．串是字符的有限序列
B．空串是由空格构成的串
C．模式匹配是串的一种重要运算
D ．串既可以采用顺序存储，也可以采用链式存储

零个字符的串称为空串，其长度为零。
空格是串的字符集合中的一个元素。

（3）串“ ababaaababaa ”的 next 数组为（C） 。
A ． 012345678999 B． 012121111212
C． 011234223456 D． 0123012322345

计算字符串的next函数值,可以参考"KMP模式匹配算法".
计算过程:
下标 j : 1 2 3 4 5 6 7 8 9 10 11 12
字符串: a b a b a a a b a b a a
next[ j ] 0 1 1 2 3 4 2 2 3 4 5 6
1)当j=1时,固定就是next[1]=0;
2)当j=2时,由1到j-1的字符串是"a",属于其他情况,固定就是next[2]=1;
3)当j=3时,由1到j-1的字符串是"ab",前缀字符"a"与后缀字符"b"不相等, 属于其他情况,所以,next[3]=1;
4)当j=4时,由1到j-1的字符串是"aba",前缀字符"a"与后缀字符"a"相等, 也就是有1个字符相等,所以,next[4]=1+1=2;
5)当j=5时,由1到j-1的字符串是"abab",前缀字符"ab"与后缀字符"ab"相等,也就是有2个字符相等,所以,next[5]=2+1=3;
6)当j=6时,由1到j-1的字符串是"ababa",前缀字符"aba"与后缀字符"aba"相等,也就是有3个字符相等,所以,next[6]=3+1=4;
7)当j=7时,由1到j-1的字符串是"ababaa",前缀字符"a"与后缀字符"a"相等,也就是有1个字符相等,所以,next[7]=1+1=2;
8)当j=8时,由1到j-1的字符串是"ababaaa",前缀字符"a"与后缀字符"a"相等,也就是有1个字符相等,所以,next[8]=1+1=2;
9)当j=9时,由1到j-1的字符串是"ababaaab",前缀字符"ab"与后缀字符"ab"相等,也就是有2个字符相等,所以,next[9]=2+1=3;
10)当j=10时,由1到j-1的字符串是"ababaaaba",前缀字符"aba"与后缀字符"aba"相等, 也就是有3个字符相等,所以,next[10]=3+1=4;
11)当j=11时,由1到j-1的字符串是"ababaaabab",前缀字符"abab"与后缀字符"abab"相等,也就是有4个字符相等,所以,next[11]=4+1=5;
12)当j=12时,由1到j-1的字符串是"ababaaababa",前缀字符"ababa"与后缀字符"ababa"相等,也就是有5个字符相等,所以,next[12]=5+1=6;

（4）串“ ababaabab ”的nextval 为（A）。
A ． 010104101 B． 010102101
C ． 010100011 D ． 010101011

下标 i : 1 2 3 4 5 6 7 8 9
字符串s: a b a b a a b a b
next [ i ]: 0 1 1 2 3 4 2 3 4
nextval[i]: 0 1 0 1 0 4 1 0 1
先计算前缀next[i]的值：
计算字符串的next函数值,可以参考"KMP模式匹配算法".
next [ i ]: 0 1 1 2 3 4 2 3 4
接下来计算nextval[i]的值：
第一位的nextval 值必定为0，第二位如果于第一位相同则为0，如果不同则为1。
第三位的next 值为1，那么将第三位和第一位进行比较，均为a，相同，则第三位的nextval 值为0。
第四位的next 值为2，那么将第四位和第二位进行比较，相同，第二位的next 值为1，则继续将第二位与第一位进行比较，不同，则第四位的nextval 值为第二位的next 值，为1。
第五位的next 值为3，那么将第五位和第三位进行比较，相同，第三位的next 值为1，则继续将第三位与第一位进行比较，相同，则第五位的nextval 值为第一位的next 值，为0。
第六位的next 值为4，那么将第六位和第四位进行比较，不同，则第六位的nextval 值为其next 值，为4。
第七位的next 值为2，那么将第七位和第二位进行比较，相同，第二位的next 值为1，则继续将第二位与第一位进行比较，不同，则第七位的nextval 值为第二位的next 值，为1。
第八位的next 值为3，那么将第八位和第三位进行比较，相同，第三位的next 值为1，则继续将第三位与第一位进行比较，相同，则第八位的nextval 值为第一位的next 值，为0。
第九位的next 值为4，那么将第九位和第四位进行比较，相同，第四位的next 值为2，则继续将第四位与第二位进行比较，相同，则第八位的nextval 值为第二位的next 值，为1。
nextval为0,1,0,1,0,4,1,0,1

（5）串的长度是指（B） 。
A ．串中所含不同字母的个数
B ．串中所含字符的个数
C．串中所含不同字符的个数
D ．串中所含非空格字符的个数

串中字符的数目称为串的长度。

（6）假设以行序为主序存储二维数组A=array[1…100,1…100] ，设每个数据元素占2 个存储单元，基地址为10，则LOC[5,5]= （B）。
A． 808 B． 818 C． 1010 D ． 1020

LOC ( i , j ) = 基地址 + ( ( i - 1 ) * m + j ) * L (L为每个元素占的存储单元)
以行序为主，则LOC[5,5]=[ （ 5-1 ） *100+ （ 5-1 ） ]*2+10=818 。

（ 7）设有数组A[i,j] ，数组的每个元素长度为3 字节， i 的值为1 ~ 8，j 的值为1 ~ 10，数组从内存首地址BA 开始顺序存放， 当用以列为主存放时， 元素A[5,8] 的存储首地址为（B）。
A． BA+141 B ． BA+180
C． BA+222 D． BA+225

LOC ( i , j ) = 基地址 + ( ( j - 1 ) * m + i ) * L (L为每个元素占的存储单元)
以列序为主，则LOC[5,8]=[ （ 8-1 ） *8+ （ 5-1 ） ]*3+BA=BA+180 。

（8）设有一个10 阶的对称矩阵A ，采用压缩存储方式，以行序为主存储， a11 为第一元素，其存储地址为1，每个元素占一个地址空间，则a85 的地址为（C） 。
A． 13 B． 32 C． 33 D． 40

这个是从k=0，1…开始计算的，题中储存的第一个元素a11的地址为1，所以将所得的结果加1

（9）若对n 阶对称矩阵 A 以行序为主序方式将其下三角形的元素(包括主对角线上所有元素) 依次存放于一维数组B[1…(n(n+1))/2] 中， 则在B 中确定aij（ iB）。
A． i*(i-1)/2+j B． j*(j-1)/2+i
C． i*(i+1)/2+j D． j*(j+1)/2+i

题中：依次存放于一维数组B[1…(n(n+1))/2] 中，可知k从1开始，故将下列公式的结果加1，又因为i

（10）二维数组A 的每个元素是由10 个字符组成的串，其行下标i=0,1, , ,8, 列下标j=1,2, , ,10 。若A 按行先存储，元素A[8,5] 的起始地址与当A 按列先存储时的元素（B）的起始地址相同。设每个字符占一个字节。
A． A[8,5] B． A[3,10] C. A[5,8] D． A[0,9]

设数组从内存首地址M 开始顺序存放，若数组按行先存储，元素A[8,5] 的起始地址为： M+[ （ 8-0 ） *10+ （ 5-1 ） ]*1=M+84 ；若数组按列先存储，易计算出元素A[3,10] 的起始地址为： M+[ （ 10-1 ） *9+( 3-0 ) ]*1=M+84 。

（11）设二维数组A[1… m ， 1… n] （即m 行n 列）按行存储在数组B[1… m*n] 中，则二维数组元素A[i,j] 在一维数组B 中的下标为（A） 。
A ． (i-1)n+j B． (i-1)n+j-1 C． i(j-1) D ． jm+i-1

按行存储, 一共有( i - 1) 行存满，再加 j 个元素就是了。

（12）数组A[0…4,-1…-3,5…7] 中含有元素的个数（B） 。
A． 55 B ． 45 C． 36 D． 16

三维数组，共有533=45 个元素。

（13）广义表A=(a,b,(c,d),(e,(f,g))) ，则Head(Tail(Head(Tail(Tail(A))))) 的值为（D） 。
A． (g) B ． (d) C． c D． d

Tail(A)=(b,(c,d),(e,(f,g))) ； Tail(Tail(A))=( (c,d),(e,(f,g))) ； Head(Tail(Tail(A)))=(c,d) ； Tail(Head(Tail(Tail(A))))=(d) ； Head(Tail(Head(Tail(Tail(A)))))=d 。

（14）广义表((a,b,c,d)) 的表头是（C） ，表尾是（B） 。
A． a B ． ( ) C ． (a,b,c,d) D ． (b,c,d)

表头为非空广义表的第一个元素，可以是一个单原子，也可以是一个子表，((a,b,c,d)) 的表头为一个子表(a,b,c,d) ；表尾为除去表头之外，由其余元素构成的表，表为一定是个广义表， ((a,b,c,d)) 的表尾为空表( ) 。

（15）设广义表L=((a,b,c)) ，则L 的长度和深度分别为（C） 。
A． 1 和1 B． 1 和3 C． 1 和2 D． 2 和3

广义表的深度是指广义表中展开后所含括号的层数，广义表的长度是指广义表中所含元素的个数。根据定义易知L 的长度为1，深度为2。

2．应用题

（1）已知模式串t=‘ abcaabbabcab ’写出用KMP法求得的每个字符对应的next 和nextval函数值。

/*
模式串t 的next 和nextval 值如下：
下标j       1 2 3 4 5 6 7 8 9 10 11 12
模式串t	    a b c a a b b a b c   a  b
next[j]		0 1 1 1 2 2 3 1 2 3   4  5
nextval[j]  0 1 1 0 2 1 3 0 1 1   0  5
*/

（2）设目标为t= “ abcaabbabcabaacbacba ” , 模式为p= “ abcabaa ”
①计算模式p 的naxtval 函数值；
②不写出算法, 只画出利用KMP算法进行模式匹配时每一趟的匹配过程。

/*
1.p 的nextval 函数值为0110132 (p 的next 函数值为0111232)
2.利用KMP(改进的nextval) 算法，每趟匹配过程如下
第一趟匹配： abcaabbabcabaacbacba
abcab(i=5,j=5)
第二趟匹配： abcaabbabcabaacbacba
abc(i=7,j=3)
第三趟匹配： abcaabbabcabaacbacba
a(i=7,j=1)
第四趟匹配： abcaabbabcabaac bacba
( 成功) abcabaa(i=15,j=8)
*/

（3）数组A 中，每个元素A[i,j] 的长度均为32 个二进位, 行下标从-1 到9，列下标从1到11 ，从首地址S 开始连续存放主存储器中，主存储器字长为16 位。求：
①存放该数组所需多少单元？
②存放数组第4 列所有元素至少需多少单元？
③数组按行存放时，元素A[7,4] 的起始地址是多少？
④数组按列存放时，元素A[4,7] 的起始地址是多少？

每个元素32 个二进制位，主存字长16 位，故每个元素占2 个字长，行下标可平移至1到11 。
（ 1） 242 （ 2）22 （ 3） s+182 （ 4） s+142

(4) 请将香蕉banana 用工具 H( ) — Head( ) ， T( ) — Tail( ) 从L 中取出。
L=(apple,(orange,(strawberry,(banana)),peach),pear)
答案： H（ H（ T（ H（ T（ H（ T（ L）））））））

3．算法设计题

（1）写一个算法统计在输入字符串中各个不同字符出现的频度并将结果存入文件（字符串中的合法字符为A-Z 这26 个字母和0-9 这10 个数字）。
[ 题目分析]

由于字母共26 个，加上数字符号10 个共36 个，所以设一长36 的整型数组，前10 个分量存放数字字符出现的次数， 余下存放字母出现的次数。从字符串中读出数字字符时，字符的ASCII 代码值减去数字字符‘0’的ASCII 代码值，得出其数值(0…9) ，字母的ASCII 代码值减去字符‘ A’的ASCII 代码值加上10 ，存入其数组的对应下标分量中。遇其它符号不作处理，直至输入字符串结束。

[ 算法描述]

void Count (){	// 统计输入字符串中数字字符和字母字符的个数。
	int i, num[36];
	char ch ;
	for ( i ＝ 0; i<36 ; i++ ) num[i] ＝0; // 初始化
	while ((ch ＝ getchar()) != '#'){ 	// ‘ # ’表示输入字符串结束。
		if ('0'<=ch<=' 9'){ i=ch － 48;num[i]++ ;} // 数字字符
		else if ('A' <=ch<= 'Z'){ i=ch-65+10;num[i]++;} // 字母字符
	}
	for (i=0 ; i<10 ;i++ ) // 输出数字字符的个数
		cout<<"数字" <<i<< "的个数="<<num[i]<<endl;
	for (i ＝ 10; i<36 ; i++ )		// 求出字母字符的个数
		cout<<"字母字符" <<i+55<< "的个数="<<num[i]<<endl;
}

（2）写一个递归算法来实现字符串逆序存储，要求不另设串存储空间。
[ 题目分析]

实现字符串的逆置并不难，但本题“要求不另设串存储空间”来实现字符串逆序存储，即第一个输入的字符最后存储，最后输入的字符先存储，使用递归可容易做到。

[ 算法描述]

void InvertStore( char A[]){	// 字符串逆序存储的递归算法。
	char ch;
	static int i = 0;		// 需要使用静态变量
	cin>>ch;
	if (ch!= '.') {			// 规定'.' 是字符串输入结束标志
		InvertStore(A);
		A[i++] = ch;		// 字符串逆序存储
	}
	A[i] = '\0'; 			// 字符串结尾标记
}

（3）编写算法，实现下面函数的功能。函数void insert(chars,chart,int pos) 将字符串t 插入到字符串s 中，插入位置为pos 。假设分配给字符串s 的空间足够让字符串t插入。（说明：不得使用任何库函数）
[ 题目分析]

本题是字符串的插入问题，要求在字符串s 的pos 位置，插入字符串t 。首先应查找字符串s 的pos 位置，将第pos 个字符到字符串s 尾的子串向后移动字符串t 的长度，然后将字符串t 复制到字符串s 的第pos 位置后。
对插入位置pos 要验证其合法性，小于1 或大于串s 的长度均为非法，因题目假设给字符串s 的空间足够大，故对插入不必判溢出。

[ 算法描述]

void insert(char *s,char *t,int pos){	
// 将字符串t 插入字符串s 的第pos 个位置。
	int i=1,x=0; 
	//p ， q 分别为字符串s 和t 的工作指针
	char *p=s,*q=t; 
	if(pos<1) {cout<< "pos 参数位置非法" <<endl;exit(0);}
	while(*p!= '0'&&i<pos) {p++;i++;} 		// 查pos 位置
	// 若pos 小于串s 长度，则查到pos 位置时， i=pos 。
	if(*p == '/0') {cout<<pos<<" 位置大于字符串s 的长度";exit(0);}
	else 			// 查找字符串的尾
		while(*p!= '/0') {p++; i++;} // 查到尾时， i 为字符‘ \0 ’的下标， p 也指向‘ \0 ’。
	while(*q!= '\0') {q++; x++; } // 查找字符串t 的长度x，循环结束时q 指向'\0' 。
	for(j=i;j>=pos ;j--){*(p+x)=*p; p--;}// 串s 的pos 后的子串右移，空出串t 的位置。
	q--;	 // 指针q 回退到串t 的最后一个字符
	for(j=1;j<=x;j++) *p--=*q--; 	// 将t 串插入到s 的pos 位置上
}

（4）已知字符串S1 中存放一段英文，写出算法format(s1,s2,s3,n), 将其按给定的长度n 格式化成两端对齐的字符串S2, 其多余的字符送S3。
[ 题目分析]

本题要求字符串s1 拆分成字符串s2 和字符串s3 ，要求字符串s2“按给定长
度n 格式化成两端对齐的字符串” ，即长度为n 且首尾字符不得为空格字符。算法从左到右扫描字符串s1 ，找到第一个非空格字符，计数到n ，第n 个拷入字符串s2 的字符不得为空格，然后将余下字符复制到字符串s3 中。

[ 算法描述]

void format (char *s1,*s2,*s3){
// 将字符串s1 拆分成字符串s2 和字符串s3 ，要求字符串s2 是长n 且两端对齐
	char *p=s1, *q=s2;
	int i=0;
	while(*p!= '\0' && *p== ' ') p++;// 滤掉s1 左端空格
	if(*p== '\0') {cout<<" 字符串s1 为空串或空格串"<<endl;exit(0); }
	while( *p!='\0' && i<n){*q=*p; q++; p++; i++;}
	// 字符串s1 向字符串s2 中复制
	if(*p =='\0'){cout<<" 字符串s1 没有"<<n<<" 个有效字符"<<endl; exit(0);}
	if(*(--q)==' ' ){ // 若最后一个字符为空格，则需向后找到第一个非空格字符
		p-- ; //p 指针也后退
		while(*p==' '&&*p!='\0') p++;// 往后查找一个非空格字符作串s2 的尾字符
		if(*p=='\0'){cout<<"s1 串没有"<<n<<" 个两端对齐的字符串"<<endl; exit(0);}
		*q=*p; // 字符串s2 最后一个非空字符
		*(++q)='\0'; // 置s2 字符串结束标记
	}
	*q=s3;p++; // 将s1 串其余部分送字符串s3 。
	while (*p!= '\0') {*q=*p; q++; p++;}
	*q='\0'; // 置串s3 结束标记
}

（5）设二维数组a[1…m, 1…n] 含有m*n 个整数。
①写一个算法判断a 中所有元素是否互不相同?输出相关信息(yes/no) ；
②试分析算法的时间复杂度。
[ 题目分析]

判断二维数组中元素是否互不相同， 只有逐个比较, 找到一对相等的元素， 就可结论为不是互不相同。如何达到每个元素同其它元素比较一次且只一次？在当前行，每个元素要同本行后面的元素比较一次（下面第一个循环控制变量p 的for 循环） ，然后同第i+1行及以后各行元素比较一次，这就是循环控制变量k 和p 的二层for 循环。

[ 算法描述]

int JudgEqual(ing a[m][n],int m,n){
// 判断二维数组中所有元素是否互不相同，如是，返回1；否则，返回0。
	for(i=0;i<m;i++){
		for(j=0;j<n-1;j++){
			for(p=j+1;p<n;p++) 		// 和同行其它元素比较
				if(a[i][j]==a[i][p]) {cout<< "no" ; return(0); }
				// 只要有一个相同的，就结论不是互不相同
				for(k=i+1;k<m;k++) // 和第i+1 行及以后元素比较
					for(p=0;p<n;p++)
						if(a[i][j]==a[k][p]) {cout<<"no" ; return(0); }
		}
	}
	cout<< "yes" ; 
	return(1); // 元素互不相同
}

二维数组中的每一个元素同其它元素都比较一次，数组中共mn 个元素，第1 个元素同其它mn-1 个元素比较，第2 个元素同其它mn-2 个元素比较， , ，第mn-1 个元素同最后一个元素(mn) 比较一次, 所以在元素互不相等时总的比较次数为 (mn-1)+(mn-2)+ ,+2+1=（ mn）(mn-1)/2 。在有相同元素时, 可能第一次比较就相同, 也可能最后一次比较时相同, 设在(mn-1) 个位置上均可能相同, 这时的平均比较次数约为（ mn ）(mn-1)/4 ，总的时间
复杂度是O(n 4) 。

(6) 设任意n 个整数存放于数组A(1:n) 中，试编写算法，将所有正数排在所有负数前面（要求算法复杂度为0(n) ）。
[ 题目分析]

本题属于排序问题，只是排出正负，不排出大小。可在数组首尾设两个指针i 和j ，i 自小至大搜索到负数停止， j 自大至小搜索到正数停止。然后i 和j 所指数据交换，继续以上过程，直到 i=j 为止。

[ 算法描述]

void Arrange(int A[],int n){
//n 个整数存于数组A 中，本算法将数组中所有正数排在所有负数的前面
	int i=0,j=n-1,x; 	
	while(i<j){
		while(i<j && A[i]>0) i++;
		while(i<j && A[j]<0) j--;
		if(i<j) {x=A[i]; A[i++]=A[j]; A[j--]=x; }	// 交换A[i] 与A[j]
	}
}