2020年春季学期 计算机学院《软件构造》课程——Lab1总结

1 实验目标概述

本次实验通过求解三个问题,训练基本 Java编程技能，能够利用 Java OO开发基本的功能模块，能够阅读理解已有代码框架并根据功能需求补全代码，能够为所开发的代码编写基本的测试程序并完成测试，初步保证所开发代码的正确性。 另一方面 ，利用 Git作为代码配置管理的工具，学会 Git的基本使用方法。
1基本的 Java OO编程
2基于 Eclipse IDE进行 Java编程
3基于 JUnit的测试
4基于 Git的代码配置管理

2 实验环境配置

2.1实验环境的配置方法与过程

(1) 阅读 http://web.mit.edu/6.031/www/fa19/getting-started/ ，按该 页面列出
的指南，在本地机器安装相应的开发环境（ JDK、 Eclipse、 Git）并熟练
掌握它们的配置过程。
(2) 可以从 http://web.mit.edu/6.031/www/sp17/getting-started/eclipse-faq/ 获取更多的 Eclipse帮助。
(3) 阅读 http://web.mit.edu/6.031/www/fa19/classes/02-basic-java/ 了解 Java的基本 编程 特性。
(4) 关于 Git的学习手册：https://git-scm.com/book/en/v2 、 https://git-scm.com/book/zh/v2可使用 https://www.shiyanlou.com/courses/4 提供的在线实验环境进行 Git练习。
(5) 阅读 http://web.mit.edu/6.005/www/fa16/psets/ps0/#unit_testing ，了解 单元测试和 JUnit工具 。
(6) 阅读 https://github.com/junit-team/junit4/wiki/Download-and-Install 并 在 自己的 Eclipse IDE中安装配置 JUnit。
(7) 阅读 https://github.com/junit-team/junit4/wiki/Getting-started 了解如何 使用 JUnit为 Java程序编写测试代码 并执行测试 。

2.2实验环境配置过程中遇到的问题和困难

2.2.1.java环境的配置

由于我们实验采用java作为开发的语言，java不同于之前我们所用到的c语言java是一种面向对象的语言，其原理主要在于Java的虚拟机JVM，而且想要使用java开发我们需要安装并配置java环境，即JDK，我们采用JDK1.8版本作为开发工具。但是我们所提供的有关MIT的实验指导全英版本，首先理解并按照步骤操作成为我的第一个问题。
其次在下载并安装jdk1.8之后，需要在本地设置一些环境变量，开始时我按照教程以及一些经验来操作但发现并不能运行Java环境，在老师的指导下发现了自己的问题并成功配置环境变量之后，运行javac。下面是环境配置的三个变量以及截图：


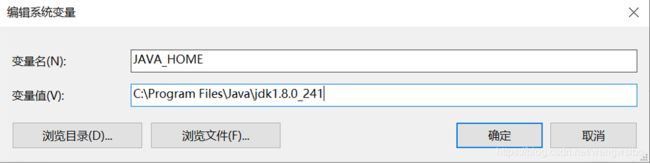
但是遇到了环境变量JAVA在电脑关机重启后就会失效的问题，在CSDN上
找到了解决方案，参考文章：https://blog.csdn.net/zhijingmu/article/details/80647174 把PATH变量分成数行加入后问题解决。到此java环境配置完成。

2.2.2.eclipse的安装与配置

在java的环境配置完成之后eclipse的安装与配置就十分顺畅，在这里我并没有选择从MIT的课程界面上的网址下载eclipse，而是到官网下载并安装，当我们的java环境在电脑上正常运行时候，直接安装并运行eclipse，这里没有出现较大的问题，这里有一个小技巧可以打开eclipse.ini并根据计算机的内存适当修改Xms与XMx可以加快运行速度。

2.2.3.Git及Git bash的安装与使用

1.https://git-scm.com/ 在官网中下载git并安装

2.配置path：在环境变量中配置

3.配置git：用户名和邮箱
在桌面上右键选择git-Bash here
输入以下内容
git config --global user.name "xxxxx”
git config --global user.email xxxxxxx
4.配置git与远程库连接：ssh
为了在本地和远程仓库之间进行 免密钥登录，可以配置ssh。
配置ssh:先在本地配置，再发送给远程
先查看是否有.ssh文件输入命令：cd ~/.ssh 并在如下所示的路径下找到这个id_rsa.pub文件。

发送给远程：
打开：https://github.com/settings/keys


此时git已经配置好了，下面可以将一个工程设置为一个git所管理的仓库了，在终端控制本地与远程之间的交互，不断提交自己程序的各个版本。

3 实验过程

3.1 Magic Squares

实验任务理解：检验矩阵是否是幻方矩阵。首先要检验文本中输入数据是否满足规范（包括是否构成方阵、是否按要求将数据以制表符隔开、是否包含小数和负数、是否有非法字符等），在满足规范的前提下，检验该方阵是否每行、每列和每条对角线上的元素相加都相等。最后，根据给出的参数生成一个新的矩阵存入第六个文本中并检验它。
任务考察点：Java基本语法，文件读写，判断输入的合法性，简单的异常处理

3.1.1 isLegalMagicSquare()

3.1.1.1 处理输入文件并分割

我们选择通过FileReader类的readline方法来实现从文本读取字符串，并且每次读取一行就对其进行非法字符的检查如图所示，如果不是以‘\t’或’\n’来分割字符则会打印提示信息并退出，同时如果检测到代表小数的’.’和代表负数的’-’同样会打印提示信息退出，并且同时记录所读入的行数。此阶段完成之后满足条件的输入文件会被组织成一个长字符串保存在inputdata中。

之后我们用String的spilt方法先对长字符串以’\n’来分割，得到一个字符串数组每一个记录里输入的一行，下面我们循环这个字符串数组，即逐行解析输入文件，每行用spilt方法以’\t’来分割之后立即转换成整数存在我们所建立的整形数组的相应位置，随着行数的增加我们检查每一行所分割得到的数字的个数（程序中的colnum），分为linenum>colnum和linenum
值得一提的是，由于我们是用了文件的读写方法，这里有可能会抛出异常，找不到文件等异常，因此我们对整个isLegalMagicSquare()采用try…catch结构来处理抛出的异常。

3.1.1.2 幻方条件判断

在得出整形矩阵之后判断幻方变得十分简单，只需要将行之和，列之和。对角线之和分别计算并存在三个数组中，判断这三个数组的所有元素都相等才可以，思路很简单不再赘述。

3.1.1.3 5个txt的结果显示

在main方法中分别调用isLegalMagicSquare()函数五次每次以一个文件的路径作为参数得出五个结果，并提示打印即可，下面是对实验所提供的五个文件的结果的展示，1,2是一个幻方，第3个文件在19行出存在数据不整齐，不能构成矩阵的情况，第4个文件第三行存在不满足要求的数字出现，第5个文件在121行存在不以’\t’分割字符串的问题。

3.1.2 generateMagicSquare()

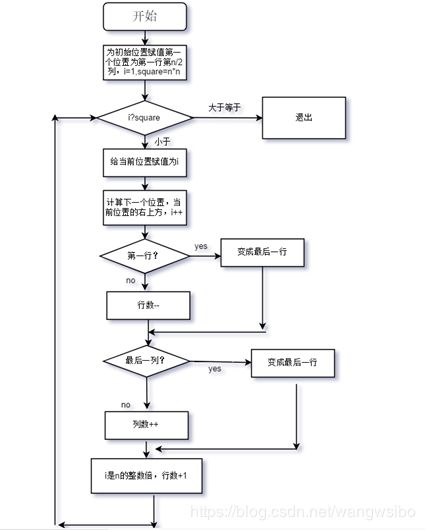
3.1.2.1 程序的流程图解释

3.1.2.2 对该函数做扩展

产生这个错误的原因为：代码第17行出现了一个数组下标越界的错误，产生的异常原因时函数在处理的时候没有考虑到n为偶数的情况，magic[row][col]=I;在n递增之后会超过数组的大小，产生越界访问。

此异常的含义是数组的大小非法，产生原因时，当n为负数时，创建二维数组的时候会尝试创建负维度的矩阵，此时是非法的。
对给出函数的扩展局部代码如下：

3.1.2.3 产生一个新的幻方矩阵并用第一个函数检验

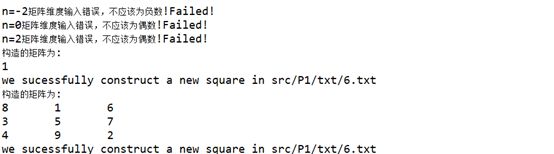
在上述扩展的函数基础上实现将生成的矩阵写入文件6.txt，实现起来较为简单，加入如下操作就可以实现，检验的工作我放在了main函数中实现。

在main中测试所要求的5个txt之后我们执行一个循环来对generateMagicSquare在n分别为-2 、0 、2 、1 、3 、13对函数进行测试，具体代码以及在控制台上得到的结果如下图，最后存放在6.txt中的矩阵是n=13时的矩阵。

3.2 Turtle Graphics

人物理解：该任务要根据代码注释提示补全代码从而实现一个完整的绘制工具Trurtle Graphics。主要考察：计算几何基础知识，正多边形的内角外角，java函数调用绘制多边形，计算向量之间的夹角，计算凸包，并使用Junit进行单元测试。

3.2.1 Problem 1: Clone and import

从本地创建git仓库：
1.git init初始化本地仓库
2.git remote add origin 添加远程库源
3.在远程仓库创建master分支
4.git pull origin master将远程仓库同步到本地
5.git add-> git commit-> git push 将本地文件加入本地仓库，将本地仓库同步到远程仓库。

3.2.2 Problem 3: Turtle graphics and drawSquare

这个任务非常简单，用于熟悉turtle的一些基本操作，包括直线行走以及旋转，重复四次前进转弯90就行了。结果如下图：

3.2.3 Problem 5: Drawing polygons

这个任务考察多边形角与边的关系，根据我们的数学知识：
正多边形的内角和 = 180°×（n-2) (n为正整数且大于2,n是正多边形的边数)=n× x
而x就是我们要求的角度。写成表达式即可：

而drawRegularPolygon函数主要调用上一个函数来计算每次转动的角度，循环sides即可，具体函数如下：

在main()中调用此方法效果图：

3.2.4 Problem 6: Calculating Bearings

注意到这个函数的规约中可以从中得到提示，我们阅读java中Math库中的atan2方法：
atan2() 方法用于将矩形坐标 (x, y) 转换成极坐标 (r, theta)，返回所得角 theta。该方法通过计算 y/x 的反正切值来计算相角 theta，范围为从 -pi 到 pi。
因此我们根据几何关系可以很简单得得到所要旋转的弧度为：
(Math.atan2((targetY-currentY),(targetX-currentX))
再调用math.todegrees方法转为角度值。
注意到我们所旋转的角度在currentBearing较大时可能为负值不符合要求，因此需要在计算结束后加以判断，+360。函数如下：

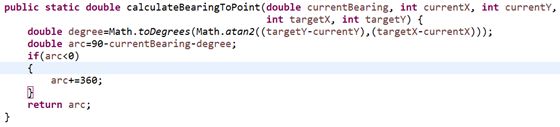
在得到calculateBearingToPoint之后，calculateBearings变得十分简单，首先这个函数的参数是一个Point 的List，因此我们需要每次重新计算一个currentBearing，这个角度是由上一次的currentBearing和上一次所转动的角度所共同决定，只需要再循环时加以更新计算即可，代码如下：

3.2.5 Problem 7: Convex Hulls

总体来说这个任务是我认为的Lab1中最难的任务，在设计完前面的方法时候算法并不算太难理解，但是实现过程中仍然出现许多问题，其中一个原因就是对java中的collection不怎么熟悉，而且第一次设计时未注意到一条边上的两个点的取舍。
首先我们看一看凸包的定义：
凸包（Convex Hull）是一个计算几何（图形学）中的概念。在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称为X的凸包。X的凸包可以用X内所有点(X1，…Xn)的凸组合来构造.在二维欧几里得空间中，凸包可想象为一条刚好包著所有点的橡皮圈。用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边形，它能包含点集中所有的点。–百度百科

在MIT的作业指导书中有提示我们使用的方法是礼品包装的方法，经过阅读以及查阅一些资料，发现凸包问题是算法竞赛常见的一个问题，解决的方法也很多，而在这个实验中这个方法确实是最方便的，因为他用到了我们所设计的函数calculateBearingToPoint。
礼品包装法原理：
卷包裹法的原理比较简单：先找一个最边缘的点（一般位于最下方，如果有多个点，则选择最左方的点），假设有一条绳子，以该点为端点向右边逆时针旋转直到碰到另一个点为止，此时找出凸包的一条边；然后再用新找到的点作为端点，继续旋转绳子，找到下一个端点；重复这一步骤直至围成一个凸多边形，即可得到这个点集的凸包。卷包裹法的时间复杂度为O（n^2）。而这个思想在实现中正用到了calculateBearingToPoint，我们从一个点开始计算到各个其他点的旋转角度，选择最小的角度的点作为下一个基准点，重复以上动作指导回到最初点。
所以主要分为下面三个步骤：
1.根据各个点的坐标计算出当前所有点中最左下角的点。
2.从这个点开始执行循环，每次循环找到calculateBearingToPoint最小的点，add到返回set中
3.结束循环，set中为所有点集合
注意TIPS：
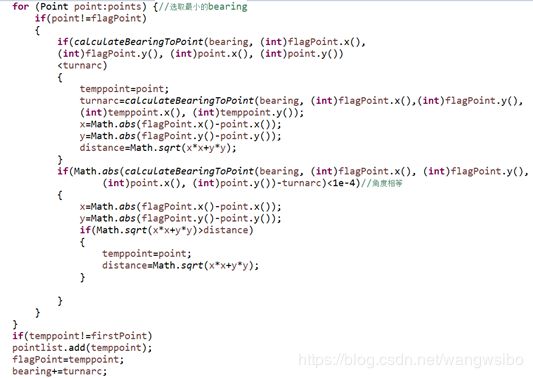
其中注意点是相同转向角额点的取舍，在循环中设置一个distance变量记录当前目标点的距离，如果之后出现了新的目标点，就用distance和计算得到的当前点的距离distance来比较进行取舍。我们选择离基准点远的点加入集合。
下面是实现的代码的一些重要部分：

3.2.6 Problem 8: Personal art

主要想法是把之前编写的drawRegularPolygon（画多边形）函数，和改变颜色的功能利用起来，采用数组+随机数的方法进行颜色的随机变化，总体为四个车轮，每个车轮的构造方法也较为简单，循环画三角形，只是每次有一些偏差即可。代码如下：

3.2.7 Submitting

如何通过Git提交当前版本到GitHub上你的Lab1仓库。
git add-> git commit-> git push 将本地文件加入本地仓库，将本地仓库同步到远程仓库。演示图如下：

3.3 Social Network

任务理解：实现Person和FriendshipGraph两个类，模拟社交网络，提供添加节点（人），节点之间添加边（社交关系），通过BFS计算两节点之间最短路的功能。
主要考点：java类的实现，java基本数据结构，BFS求最短路。

3.3.1 设计/实现FriendshipGraph类

3.3.1.1addVertex方法

首先建立一个list存储已经加入图中的各个节点，构造一个get函数来访问它。
接着设计addVertex方法，这个方法较为简单，主要在于对与不合理情况的判断，当加入的person是已经加入过的，就不再加入打印提示信息返回。当加入了另一个person但是他的名字与我们list中的一个person名字相同，此时与实验要求的spec所违背，这时需要打印提示信息并返回false且直接退出exit(-1)。其余情况就在listofpersons中加入新的点即可。

3.3.1.2addEdge方法

1.判断所加入的两点是否都在listofpersons中，不是则打印提示信息返回false
2.在personA的朋友列表中寻找是否已经添加过该关系，如果已经存在此关系，打印提示信息并返回false。
3.如果personA==personB，打印提示信息“不能添加到自身的边”，返回false
4.其他情况在A的friends中加入B即可

3.3.1.3getDistance方法

思路与步骤
1.将图中的person及其朋友的list抽取出来构建一个邻接矩阵所表示的图
2.由于图中边的权重均为1，因此不必使用我们在数据结构中所学到的迪杰斯特拉算法，使用BST广度优先搜索就可以，在找到另一个点时算法结束，否则结束时返回-1，需要注意的是在搜索时记录搜索的层数作为路径长度
3使用java中collection中的Queue queue=new LinkedList();//创建队列，这样会比自己手动构建队列方便并且安全性高
4.返回路径长度即可
注：BST算法在数据结构中属于较为简单算法，这里不再赘述，主要思想就是从头开始进队列，每当队首的元素要出栈时，将它所连接的所有点入队。
主要代码如下：

3.3.2 设计/实现Person类

首先分析Person类的功能与职责。

1. private String name存放当前Person的名字
2. private List friendsofperson存放当前节点为起始点的所有出边的另一端的Person。
   3.加入friend。具体实现如下：
   

3.3.3 设计/实现客户端代码main()

由于实验指导书中已经给出一个简单的main()客户端的例子，这里main仅仅是一个简单的示例就不做过多的更改与扩展，采用指导书中所给出的的main()方法作为客户端，并会在test中对整个程序进行更加完备的测试。
在这里回答所提出的两个问题，并已经在程序中做出相应的扩展
1.运行的结果理论应该是：-1 -1 0 -1 运行代码所得结果与期望一致
2.我们修改addVertex函数，在对加入的person进行检查，如果这个person的name与之前我们加入过的点相同，并且不是同一个点重复加入，则判定为违反了Each person has a unique name，会打印提示信息并exit(-1)

3.3.4 设计/实现测试用例

在这个测试用例中主要实现对三个方法的测试。

1. public void addVertextest()
   这里测试包括了：
   a.正常地加入一个点 b.重复加入同一个点 c.加入一个重名的点（未测试）： 会导致程序退出 d.继续加入其他点并检查之前的点是否有影响
   测试方式：assertTrue(graph.listofpersons.contain(……))

2. public void addEdge()
这里测试包括了：
a. 测试与未加入的点连线 b. 添加自身到自身 c.正常加入两个关系
d. 加入已存在的关系 e. 加入ab之后再加入ba
测试方法：assertFalse(graph.addEdge(aPerson, dPerson))//用addEdge的返回值测试

3.public void getDistancetest()
这里测试所构建的图为：

测试方法为：assertEquals(expected distance, graph.getDistance(aPerson, aPerson))//用断言assertEquals将期望的距离与实际距离比较。
主要代码如下：

4 实验过程中遇到的困难与解决途径

6 实验过程中收获的经验、教训、感想

6.1 实验过程中收获的经验和教训

首先本次实验主要是一个熟悉与入门地位的实验，通过本次实验帮助我们快速适应java编程模式，最主要的问题还是对java语言的不熟悉，从面想过程的编程到面向对象的编程的主编没有那么快的适应，设计一个类的时候思维常常会混乱。
经验：这次实验比较大的一个经验就是java中的类库功能非常强大，面对一个问题常常有时不需要自己动手写非常繁杂的代码，由于java强大的可移植性以及接口，经常阅读相关类库的API使我们解决问题变得简单，经常查阅这类资料以及其他人的经验可以是我们的效率得到很大的提升。其次，经常测试自己的代码，想到一个bug及时修复不要因为一个小小的问题而不愿意做出大量的修改，可能这个小小的错误会导致十分严重的后果。
总的来说，软件构造的实验任务较重，需要分散一定的工作量，每天完成一些，并养成很好的git习惯，经常性提交自己的程序，通过实验的实践提升课堂上所学的内容。

6.2 针对以下方面的感受

1.Java编程语言是否对你的口味？
java编程是面向对象的编程语言，方法调用，类的设计等等都十分的方便，但是对于我来说从c语言到java的转变没有那么容易，需要不断练习，熟悉java编程特点才能更好地使用，面向对象使得抽象出来的类更加具有广泛的应用，移植性好可扩展性好，这也正是软件构造时的十分重要的质量目标，对于初学者来说需要对对查阅相关的API才能更高效的使用java。
2.关于Eclipse IDE
Eclipse功能十分强大，界面友好，特别是在调用方法时有自动补全的功能，在报错时也会给出建议的修改方案，总是是一款使用起来很方便的IDE，容易debug并且集成了一些有用的插件、框架等：junit ……
3.关于Git和GitHub
Github是基于Git的一个云端server，Git是一个分布式版本管理系统，操作简单功能强大，可以灵活看到不同的变化，回退版本，而且使用上手较为容易对于初学者来说掌握基本的版本管理的方法容易，很好的实现本地与云端的关联。当我们进行工程的时候，有了自己的代码仓库，可以很好地了解记录自己的编程进度，对于更大的工程以及软件开发项目来说，这种方便的版本配置工具尤为重要。
4.关于CMU和MIT的作业
CMU和HIT的作业做题来说实现难度并不是特别大，适合作为一个熟悉以及入门的一个实验，通过阅读英文材料以及英文的要求可以提高自己的英语理解水平，而且语言也用到java很适合这门软件构造课程。
5.关于本实验的工作量、难度、deadline
工作量月ddl较为匹配，总体来说三个任务任务量较为适中，没有感觉到特别繁忙而且三周的期限也给了我们许多发挥空间、修改时间以及宽限，主要用来熟悉以及适应java语言。
6.关于初接触“软件构造”课程
课程初期所讲的内容更多的是偏为宏观与整体，是对后面章节的总领与概述的作用，但是难面会觉得有些枯燥，概念性的内容较多，这时和其他编程语言课不同的地方，而且这门课开设的目的就是尽量脱离出语言来讲解软件构造开发的中心思想，相信经过这门课的学习我们可以对软件的一系列理论问题有一个整体初步的认识，这些知识也一定会成为以后我们进行更大的开发工作时的一个指导以及正规的道路、