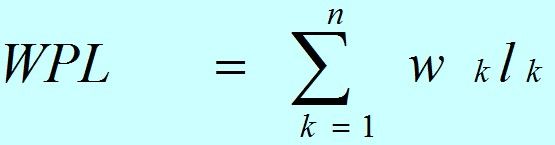转自:https://blog.csdn.net/shuangde800/article/details/7341289
一、哈夫曼树的概念和定义
什么是哈夫曼树?
让我们先举一个样例。
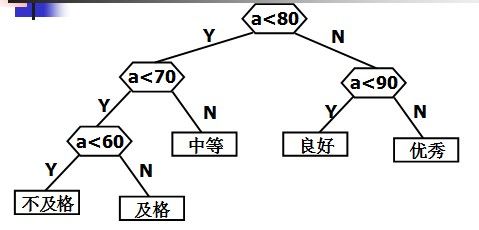
判定树:
if(score<60)
cout<<"Bad"<定义哈夫曼树之前先说明几个与哈夫曼树有关的概念:
路径:
树中一个结点到还有一个结点之间的分支构成这两个结点之间的路径。
路径长度:
路径上的分枝数目称作路径长度。
树的路径长度:
从树根到每个结点的路径长度之和。
结点的带权路径长度:
在一棵树中,假设其结点上附带有一个权值,通常把该结点的路径长度与该结点上的权值之积,称为该结点的带权路径长度(weighted path length, WPL)
什么是权值?
计算机领域中(数据结构)
权值就是定义的路径上面的值。能够这样理解为节点间的距离。通常指字符相应的二进制编码出现的概率。
至于霍夫曼树中的权值能够理解为:权值大表明出现概率大!
一个结点的权值实际上就是这个结点子树在整个树中所占的比例.
abcd四个叶子结点的权值为7,5,2,4. 这个7,5,2,4是依据实际情况得到的,比方说从一段文本中统计出abcd四个字母出现的次数分别为7,5,2,4. 说a结点的权值为7,意思是说a结点在系统中占有7这个份量.实际上也能够化为百分比来表示,但反而麻烦,实际上是一样的.
树的带权路径长度:
假设树中每一个叶子上都带有一个权值,则把树中全部叶子的带权路径长度之和称为树的带权路径长度。
设某二叉树有n个带权值的叶子结点,则该二叉树的带权路径长度记为:
公式中,wk为第k个叶子结点的权值;lk为该结点的路径长度。
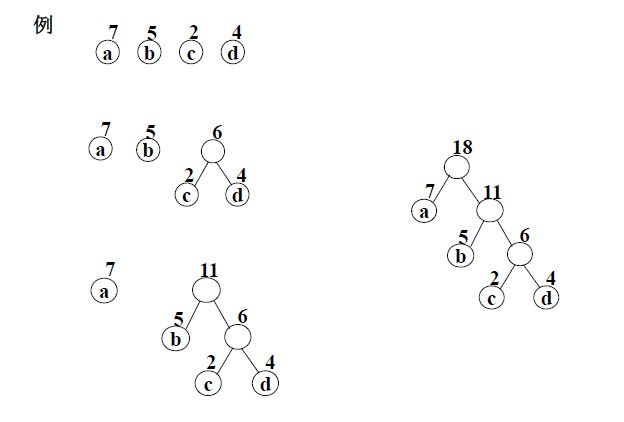
演示样例:
它们的带权路径长度分别为:
图a: WPL=5*2+7*2+2*2+13*2=54
图b: WPL=5*3+2*3+7*2+13*1=48
可见,图b的带权路径长度较小,我们可以证明图b就是哈夫曼树(也称为最优二叉树)。