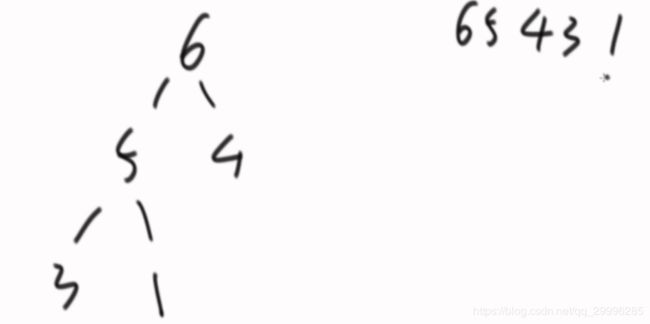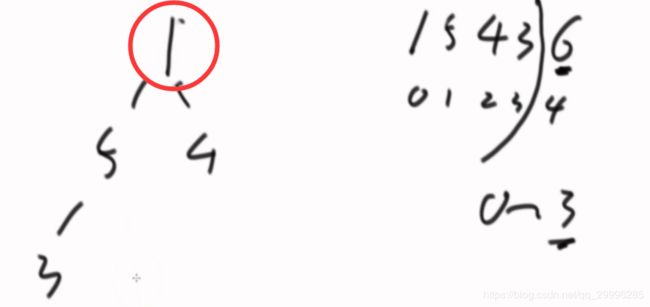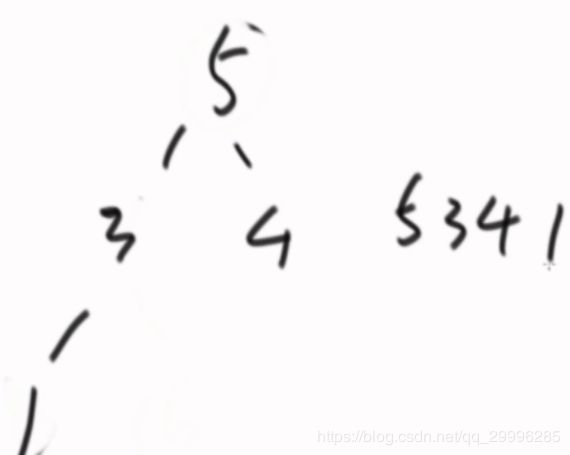左神初级班（一）

1、小和问题

换个思路，就是找一个数，他右侧有几个比他大的数，有几个，就把他乘以几。

用merge，统一用数量分批的方式去处理

类似于归并排序的思想。

为了防止溢出，所以取中值用下面的方式

归并排序之所以快，就是因为他不浪费比较。他是成组成批的比较

2、荷兰国旗问题

前置铺垫：

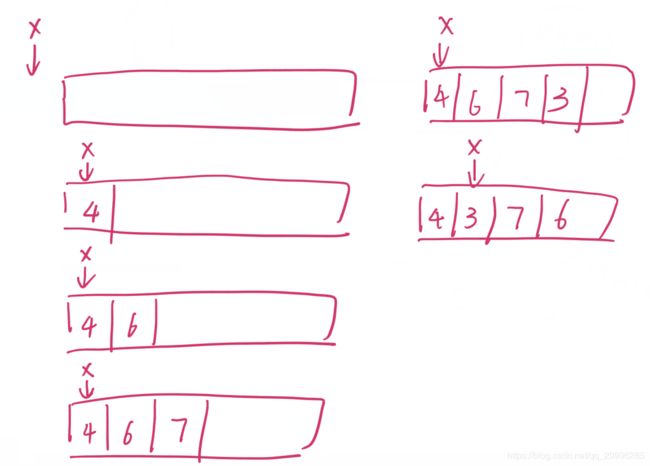
例如：输入 4,6,7,3 num的值为5.

一开始，使得x指向索引位置为-1的位置，将4放入0的位置，将4与5做比较，4小于5，则将x所指区域有一个位置的元素的值与4所在的位置进行交换，即索引位置为0的元素（因为x指向-1，他下一个元素指向的位置为0）与索引位置为0的元素（4本身的索引位置）进行交换，因此4的位置固定在了索引位置为0的地方，x指向0；

将6放入数组索引位置为1的区域，将6与5做比较，6大于5，则不进行交换；

将7放入索引位置为2的区域，由于7大于5，因此不进行交换；

将3放入索引位置为3的区域中，由于3小于5，则将3与x所指位置的下一个位置的元素（即6）进行交换，则3放在了索引位置为1的区域，6放在了索引位置为3的区域。。。整个过程如下图所示：

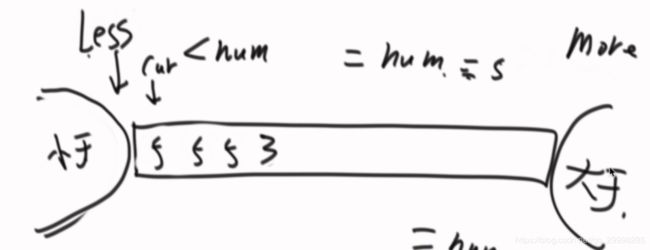
荷兰国旗问题需要两个空间，一个是小于num，一个是大于num的区域，如下图：

大于区域不用 i++，因为小于区域是推着等于区域在向右跑，因此小于的情况，i需要加加操作；如果当前值等于num，则继续向后考察；如果当前的数小于num，则将小的数发货到 less 的后面。

// 荷兰国旗.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//

#include "pch.h"
#include 
using namespace std;

void calculate(int container[], int num, int len) {
	if (container == nullptr) return;

	int less = -1, more = len;
	for (int i = 0; i < more; ) {
		if (container[i] < num) {
			less++;
			container[i]=container[less] + container[i];
			container[less] = container[i] - container[less];
			container[i] = container[i] - container[less];
			i++;
		}
		else if (container[i] > num) {
			//此时没有进行i++，使得下一轮比较的时候，i位置的元素可以与num进行比较
			//否则位置为i的元素的缺少了一次与num的比较
			more--;
			container[i] = container[more] + container[i];
			container[more] = container[i] - container[more];
			container[i] = container[i] - container[more];
		}
		else {
			i++;
		}
	}
}

int main()
{
	int container[] = { 3,4,5,0,2 };
	int num = 3;
	int len = sizeof(container) / sizeof(int);
	calculate(container, num, len);
	return 0;
}

3、经典快排

#include 
 
void quick_sort(int a[], int l, int r) {
	if (l >= r) return;
	int low = l, high=r;
	int key = a[low];
	while (low < high) {
		//从右往左找，如果该值小于key，则左移到low所指的位置
		for (;; high--) {
			if (high <= low) break;
			if (a[high] < key) {
				a[low] = a[high];
				break;
			}
		}
		//从左往右找，如果该值大于key，则右移到high所指的位置
		for (;; low++) {
			if (high <= low)break;
			if (a[low] > key) {
				a[high] = a[low];
				break;
			}
		}
	}
	//把key放在low和high重合的位置（即key应该在数组中的最终位置）
	if (low == high) a[low] = key;
 
	//分而治之
	quick_sort(a, l, low - 1);
	quick_sort(a, low+1, r);
 
}
int main()
{
	int a[10] = {2,6,3,8,9,0,1,4,7,5};
	//递归
	quick_sort(a, 0,9);
	return 0;
 
}

4、改进后的快排

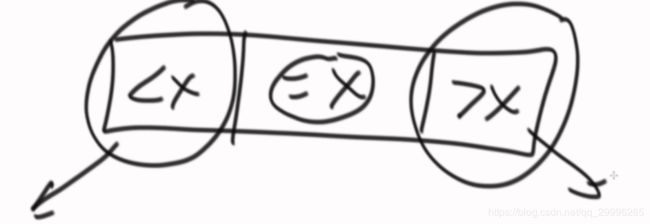
分成三个区域，小于x，等于x和大于x。然后递归排序小于x的区域和大于x的区域，而等于x的区域就不需要去动了。经典快排每次都确定一个元素的位置，而改进后的快排每次都确定所有等于x的位置。

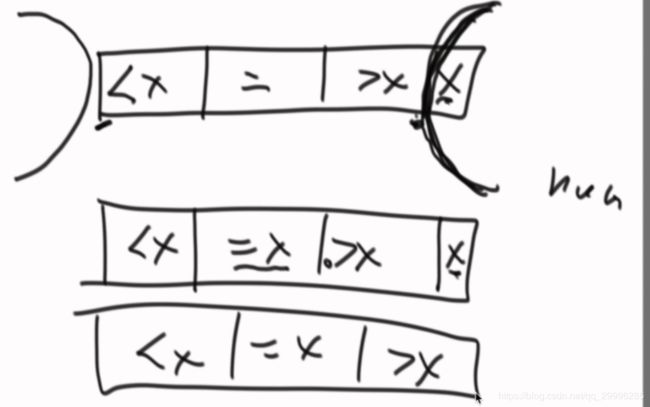
先认为的设定x为对比数据，然后将数组划分为四块（小于x，等于x，大于x和x），之后将x与大于x的第一个元素进行交换，这样就把数组分成了我们想要的上图所示的三块了。

#include 
using namespace std;

//交换arr[i]和arr[j]的值
void swap(int arr[],int i, int j) {
	int temp = 0;
	temp = arr[i];
	arr[i] = arr[j];
	arr[j] = temp;
}

//每次的对比标杆为arr[r]，即图中的x
void calculate(int arr[], int l, int r) {
	if (l >= r) return;

	int less = l - 1, more = r;
	while (l < more) {
		//当前值小于对比值（挪到less的右侧）
		if (arr[l] < arr[r]) {
			swap(arr, ++less, l++);
		}
		//当前值大于对比值（挪到more的位置）
		else if (arr[l] > arr[r]) {
			swap(arr, --more, l);
		}
		//指针向后移动
		else {
			l++;
		}
	}
	//将arr[r]移动到等于x的区域
	swap(arr, more, r);
	calculate(arr, l,less);
	calculate(arr, more+1, r);
}

int main()
{
	int container[] = { 3,0,5,0,2 };
	int len = sizeof(container) / sizeof(int);
	calculate(container, 0, len-1);
	return 0;
}

经典快排的问题——你划分出的小于区域和大于区域，有可能是偏的。如果输入的是倒序，则快排的时间复杂度就会降到O(n*n)。

5、对比归并排序和快排

1）归并排序比快速排序输你需要去准备数组，还要有数组的拷贝。merge sort输在常数项上了，merge sort的额外空间复杂度是O(n)

快排，一个while搞定

merge sort需要几个while，最后还要用一个for去拷贝过去

随机快排的空间复杂度O(logN)

快排的空间用在了记录每一次的划分点上——因为每次都要划分两块区域，需要一个空间去记录划分的那个值是多少，因此在最好情况下，你需要logN那么大的空间去记录，最差情况下是O(N)那么大的空间去进行记录。

6、堆排序

堆是一个完全二叉树（满二叉树的每个非叶子节点都有两个孩子节点，完全二叉树是前几层都是满的，左后一层叶子节点从左到右依次连续的，例如：）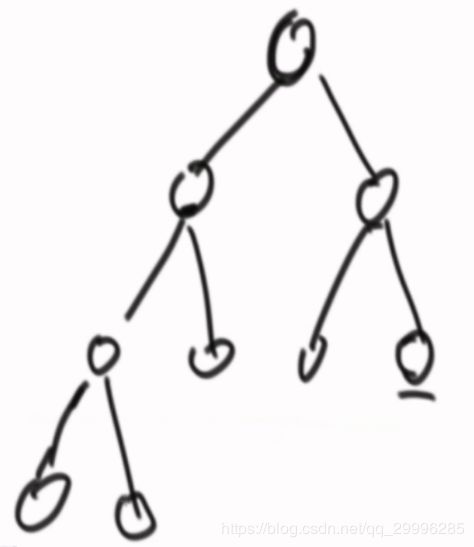

堆在实际过程中可以用数组来进行实现。位置 i 的左孩子的下标为 2* i + 1 ，右孩子下标为 2* i + 2 。堆的结构在脑海中，实际的存储形式是数组。位置为 i 的节点的父节点坐标为 (i-1)/2

-1/2=0；

堆分为大根堆和小根堆，堆就是完全二叉树。

把数组变成大根堆的过程（找索引位置为 x 的节点的父节点，父节点的索引位置为（x-1)/2 ）

1、数组：

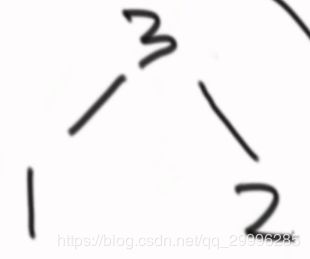
2、考查范围（0到1时的堆）：由于此时 1 的父节点坐标 x=（1-1)/2 =0 ，计算出 1 的父节点为2，2>1 ，因此 1 不与2 进行交换。

3、考查范围（0-2时的堆）：

变换过程如下：

计算 3 的父节点为（2-1)/2=0，因此3的父节点坐标为0,3 的父节点 2<3 ,此时需要将 3 和 2 的位置进行交换，数组变成

4、考查范围（0-3时的堆）：

按照上述比较方式，6先和1进行交换，数组变成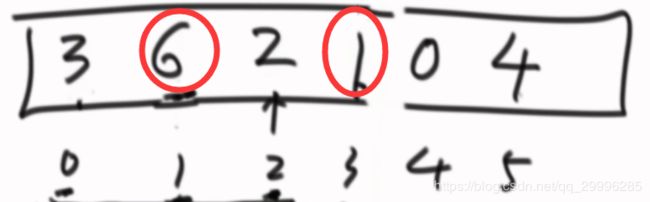，然后6 再和3进行比较，发现自己比3大，因此两个数进行交换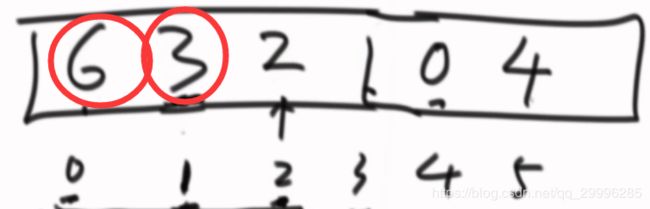

代码实现思路：给你一个数组，依次把 0到 i 的位置的数加进来，将 i 位置元素的值与其父位置元素的值进行比较，只要我大，我们就换，直到不能继续往上换位置，最终形成大根堆。

heapinsert过程

#include
using namespace std;

void swap(int arr[], int i, int father) {
	int temp = arr[i];
	arr[i] = arr[father];
	arr[father] = temp;
}

void helper(int arr[], int i) {
	//不断将其与其父节点进行比较，如果他更大，则交换两个节点的值
	while (arr[i]>arr[(i-1)/2]) {
		swap(arr, i, (i - 1) / 2);
		i = (i - 1) / 2;
	}
}

void CreatHeap(int input [], int len) {
	if ((input == nullptr) || (len == 0)) return;

	//一次获取一个元素，考察他应该在堆中的位置
	for (int i = 0; i < len; i++) {
		helper(input, i);
	}
}

int main() {

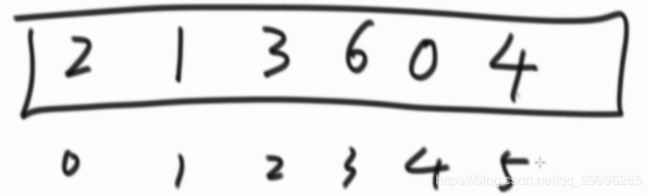
	int heap[] = { 2,1,3,6,0,4};
	int len = sizeof(heap) / sizeof(int);
	CreatHeap(heap, len);

	return 0;
}

堆中有值发生变化时

如果排好的大顶堆中，突然有一个的值变小了，则将该值与其两个孩子节点（位置 i 的左孩子的下标为 2* i + 1 ，右孩子下标为 2* i + 2 。）的值进行比较，将更大的孩子与其进行交换，然后再与新的两个孩子进行比较，依次比较至比两个孩子的值都大时，停止比较。

heapify过程

void heapify(int heap[], int index, int size) {
	//确定左孩子的节点坐标
	int left = index * 2 + 1;
	//确保不越界
	while (left <= size) {
		//选择两个孩子里面的大值
		int largest = (left + 1 < size && heap[left + 1] > heap[left]) 
			? left + 1 
			: left;

		//将大值与原index的值进行比较，取两者中最大者
		largest = heap[largest] > heap[index] ? largest : index;
		//说明index已经是最大的值了
		if (largest == index) break;
		//将最大值放在index位
		swap(heap, largest, index);
		index = largest;
		//重新确定左子树的位置，方便进行下一轮比较
		left = index * 2 + 1;
	}
}

堆排序的全过程

先让数组变成大根堆，然后将堆顶元素与堆中最后一个元素进行交换，再将堆的尺寸减一，此时最大的值就固定在数组的最后一位了。将堆中剩余的元素进行heapify。这样，每次都能确定一个值的位置。

#include "pch.h"
#include
using namespace std;

void swap(int arr[], int i, int j) {
	int temp = arr[i];
	arr[i] = arr[j];
	arr[j] = temp;
}

void helper(int arr[], int i) {
	//不断将其与其父节点进行比较，如果他更大，则交换两个节点的值
	while (arr[i]>arr[(i-1)/2]) {
		swap(arr, i, (i - 1) / 2);
		i = (i - 1) / 2;
	}
}

void heapify(int heap[], int index, int size) {
	//确定左孩子的节点坐标
	int left = index * 2 + 1;
	//确保不越界
	while (left < size) {
		//选择两个孩子里面的大值
		int largest = (left + 1 < size && heap[left + 1] > heap[left]) 
			? left + 1 
			: left;

		//将大值与原index的值进行比较，取两者中最大者
		largest = heap[largest] > heap[index] ? largest : index;
		//说明index已经是最大的值了
		if (largest == index) break;
		//将最大值放在index位
		swap(heap, largest, index);
		index = largest;
		//重新确定左子树的位置，方便进行下一轮比较
		left = index * 2 + 1;
	}
}

void CreatHeap(int input [], int len) {
	if ((input == nullptr) || (len == 0)) return;

	//一次获取一个元素，考察他应该在堆中的位置
	for (int i = 0; i < len; i++) {
		helper(input, i);
	}

	int size = len;
	swap(input, 0, --size);
	while (size > 0) {
		heapify(input, 0, size);
		swap(input, 0, --size);
	}
}

int main() {

	int heap[] = { 2,1,3,6,0,4};
	int len = sizeof(heap) / sizeof(int);
	CreatHeap(heap, len);

	return 0;
}

7、一个口，定时吐出随机数，系统希望随时找到流中吐出的所有数的中位数。

适合用堆结构去存储每一个吐出的流，因为你用普通数组存储每次吐出的数字，当系统需要中位数时，你需要先对数组进行排序，然后使用nlogn的时间来获取中位数的值。当系统对于中位数的需求很频繁的时候，用普通数组就不是一个好办法了，这时候适合用堆结构来对吐出的每一个数字进行存储。

准备两个堆，一个是大根堆，一个小根堆。我们要保持所有吐出的数字中，小的那一半在大根堆里面，大的那一半，在小根堆里面。

假设口先吐出一个 5 ，将其放入大根堆中。之后口吐出来一个 4 ，将4 与5 比较， 4 小于 5，则将 4 放入大根堆，此时两个堆的容量不平衡了，我们将大根堆的堆顶 5 弹出，存入到小根堆中作为堆顶元素。

堆顶弹出的过程：

（先交换，再减一，然后heapify。此时原来的堆顶不在堆的size范围之内，所以这个堆顶在形象上就已经不属于这个堆了，虽然他还在数组中，但是在堆的构想里面，他已经不存在了）

1、假设大根堆如此

2、先让最后一个位置的数与堆顶进行交换，然后将堆的大小减一

3、经历一场 heapify过程

回到题目中来，中位数利用大根堆的堆顶和小根堆的堆顶就可以解出来。

策略：

1、吐出的数字值小于等于大根堆的堆顶，则扔进大根堆里去；

2、如果大于大根堆的堆顶，则扔进小根堆里去；

3、如果两个堆的size之间差值大于等于2，则元素多的那个堆的堆顶弹出，放入另一个堆里面去。

实现代码：

利用STL里面的优先队列来实现大顶堆和小顶堆。先把这题解出来，然后再自己实现大顶堆和小顶堆吧。

/*
利用大顶堆和小顶堆来构造一个实时获取中位数的小工具
算法思路：
保持两个堆，堆的尺寸相差不超过1，如果超过，则将尺寸大的堆的堆顶弹出
每次获取一个数字，如果数字小于大顶堆的堆顶，则插入大顶堆中，否则插入小顶堆中
插入之后，比较两个堆的尺寸，实时调整堆

1、制作一个东西，用于获取用户的输入，输入之后自动输出当前的中位数。当输入非数字的值时，程序结束
2、构建一个大顶堆，一个小顶堆
3、用一个函数，实时将输入的数字与大顶堆和小顶堆的堆顶进行比较，用于决定插入哪一个堆中。
4、用一个函数，比较插入之后的两个堆的尺寸，如果尺寸大于1，则将大的堆的堆顶弹出，进而调整堆中的元素的位置
*/
#include "pch.h"
#include
#include
#include
using namespace std;

//返回当前中位数
int ReturnMid(priority_queue  & BigTop,
	priority_queue , greater >& SmallTop) {

	//根据size来选择反馈的实时中位数
	if (BigTop.size() - SmallTop.size() == 1) {
		return BigTop.top();
	}
	else if (SmallTop.size() - BigTop.size() == 1) {
		return SmallTop.top();
	}
	else {
		return (BigTop.top() + SmallTop.top()) / 2;
	}
}

//判断是否需要调整尺寸（注意size_t类型相减的结果）
void CheckUpSize(priority_queue  & BigTop,
	priority_queue , greater >& SmallTop) {
	
	int temp = 0;
	//尺寸有误则调整尺寸
	if (BigTop.size() - SmallTop.size() ==2) {
		temp = BigTop.top();
		BigTop.pop();
		SmallTop.push(temp);
	}
	else if (SmallTop.size() - BigTop.size() ==2) {
		temp = SmallTop.top();
		SmallTop.pop();
		BigTop.push(temp);
	}
}

//选择一个堆进行插入操作
void SelectToInsert(int input,
	priority_queue  & BigTop,
	priority_queue , greater > & SmallTop) {

	//初始情况：先将元素压入大顶堆中
	if ((BigTop.size() == 0) && (SmallTop.size() == 0)) {
		BigTop.push(input);
		return;	
	} 

	if (input <= BigTop.top()) {
		BigTop.push(input);
	}
	else {
		SmallTop.push(input);
	}
}

int main() {

	//数据输入接口
	int input = 0;
	priority_queue  BigTop;
	priority_queue , greater > SmallTop;

	while (1) {
		//如果input不是数字，则跳出循环
		cin >> input;
		if (cin.fail()) {
			//not a number
			cout << "当前输入非数字，程序退出" << endl;
			break;
		}
		//调用函数，将输入的数字与两个堆的堆顶进行比较，选择插入到哪一个堆中
		SelectToInsert( input, BigTop, SmallTop );
		CheckUpSize( BigTop, SmallTop );
		cout << ReturnMid( BigTop, SmallTop );
	}

	return 0;
}

来一个leetcode 295版本的

class MedianFinder {
private:  
    priority_queue ,less> maxHeap;           // 保存较小数  
    priority_queue,greater> minHeap;        // 保存较大数  
public:  
  
    // Adds a number into the data structure.  
    void addNum(int num) {  
        maxHeap.push(num);//往较小的数中添加  
        int t = maxHeap.top(); //返回较小数中的最大数  
        maxHeap.pop();  
        minHeap.push(t);//并将其添加到较大数中  
        int maxLen = maxHeap.size();  
        int minLen = minHeap.size();  
        if (minLen - maxLen > 0)  
        {  
            int t = minHeap.top();  
            maxHeap.push(t);  
            minHeap.pop();  
        }  
    }  
  
    // Returns the median of current data stream  
    double findMedian() {  
        if (maxHeap.size() > minHeap.size())  
            return maxHeap.top()*1.0;  
        else if (maxHeap.size() < minHeap.size())  
            return minHeap.top()*1.0;  
        else  
            return (minHeap.top() + maxHeap.top()) / 2.0;  
    }  
};

8、桶排序=基数排序+计数排序+... 不是基于比较的排序

时间复杂度O(n)

不基于比较的排序就类似于，给定一个数组，一直数组中元素的值全都处于 0到60之间，我们就可以申请一个长度为61的数组，遍历待排序的数组，遇到1的时候，就在我们申请的数组的索引位置为 1 的地方的值进行加 1 操作。如此，遍历一遍数组，我们就已经确定出每个数在数组中出现的次数，然后我们根据申请的数组中的数据来恢复，就得到了排序之后的数组。这种不急于比较的排序的时间复杂度是O(n)的。

上述排序方法就是桶排序中的计数排序。

9、给定一个数组，求排序后，相邻两数的最大差值，要求时间复杂度为O(n)，且要求不能用非基于比较的排序。

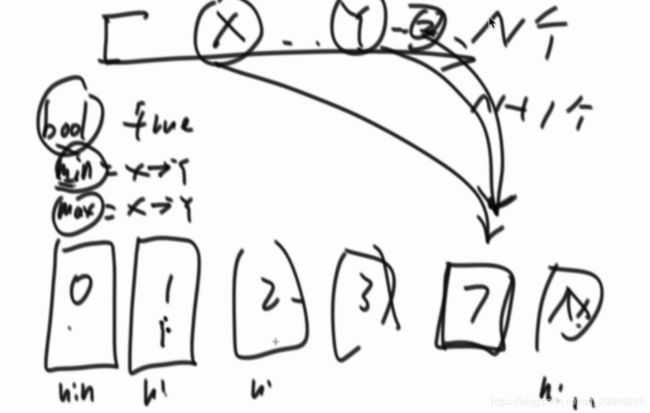
思路：遍历数组，找到最小值和最大值。如果最小值和最大值相等，则返回0. 假设数组长度为 N ，我们准备一个长度为 N+1 的数组，将最小值放在数组索引位置为 0 的位置上，最大值放在索引位置为 N 的位置上。中间的数字就放在中间的位置里。

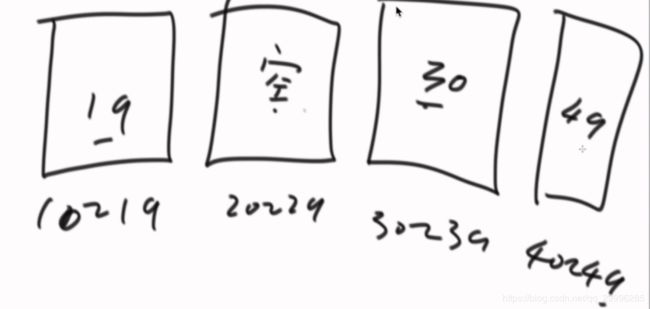
比如下图中，数组长度为 9 ，数组中元素的最大值为 99 ，最小值为 0 。我们申请一个大小为 10 的数组，则根据区间放入数组中的每个值，如下图：

有n和数和n+1个桶，最左边的桶不空，最右边的桶不空，则中间必然存在一个空桶。n个元素在排序之后，相邻两个元素可能来自同一个桶，也可能来自不同的桶，因此最大差值肯定不来自相同的桶中的两个数

数据结构：

每个桶记录三个信息：是否有数字存入；存入的最小值；存入的最大值。

然后依次计算连续的非空桶之间的差值（即前一个非空桶的最大值和后一个非空桶的最小值之间的差值）。

不去直接找空桶两侧的桶之间的差值的原因如下图所示：

实现代码：

#include "pch.h"
#include
#include
#include
using namespace std;

//计算当前数值属于哪一个桶
int calculate_inter(int num, int len, int smallest, int largest) {
	return (num - smallest)*len /(largest - smallest);
}

//计算最大的距离
void MaxGap(vectorinput) {
	int len = input.size();
	if (len == 0) return;

	//找到数组中的最大值和最小值
	int smallest = input[0], largest = input[0];
	for (int i = 0; i < len; i++) {
		if (input[i]>largest) {
			largest = input[i];
		}
		else if (input[i] < smallest) {
			smallest = input[i];
		}
	}

	//如果最大值等于最小值，则
	if (largest == smallest) {
		cout << 0; 
		return;
	} 

	//申请尺寸为 N+1 的数组(初始化长度为len+1，初值为0，不初始化的话，直接赋值赋不上)
	vectormins(len+1),maxs(len+1);
	vectorhasNum(len+1);

	//根据最大值最小值分段
	int interval =0;
	for (int i = 0; i < len; i++) {
		//确定该值属于哪一个桶(这个值是1到len之间？一会儿验证一下)
		interval = calculate_inter(input[i], len, smallest, largest);
		mins[interval] = hasNum[interval] ? min(mins[interval], input[i]) : input[i];
		maxs[interval] = hasNum[interval] ? max(maxs[interval], input[i]) : input[i];
		hasNum[interval] = true;
	}

	//找最大的gap
	int answer = 0, nowLargest = maxs[0];
	for (int i = 1; i <= len; i++) {
		if (hasNum[i]) {
			answer = answer < mins[i] - nowLargest ? mins[i] - nowLargest : answer;
			nowLargest = maxs[i];
		}
	}
	cout << answer;
}

int main(int argc, char* argv[])
{
	vectorinput = { 0,99,5,22,66,44,27,43,0,23,75,34,17,53,89,34,66,27,85,42 };
	MaxGap(input);
	return 0;
}

10、用数组实现大小固定的队列和栈

一、数组实现栈

#include "pch.h"
#include
#include

template
class MyStack {
public:
	MyStack(int i = 0);
	~MyStack();

	void push(T input);
	T pop();
	const T top ();
	const bool empty();
	const int getsize ();

private:
	T *num;
	int size;
};

template inline
MyStack::MyStack(int i):size(i) {
	num = new T[10];
}

template inline
MyStack::~MyStack() {
	delete[] num;
}

template inline
void MyStack::push(T input) {
	if (size >= 10) {
		std::cout << "stack is full" << std::endl;
		return;	
	}
	num[size++] = input;
}

template inline
T MyStack::pop() {
	if (size <= 0) {
		std::cout << "stack is empty" << std::endl;
		return 0;
	}

	return num[--size];
}

template inline 
const T MyStack::top () {
	if (size <= 0) {
		std::cout << "stack is empty" << std::endl;
		return 0;
	}

	T temp = size-1;
	return num[temp];

}

template inline
const bool MyStack::empty() {
	if (size == 0) return true;
	else return false;
}

template inline
const int MyStack::getsize() {
	return size;
}


int main()
{
	MyStack stack;
	stack.push(2);
	stack.push(3);
	stack.push(3);	
	stack.push(3);
	bool em=stack.empty();
	int size=stack.getsize();
	int top=stack.top();
	stack.pop();
	return 0;
}

二、数组实现队列

使用两根指针，分别指向“队头”和“队尾”，size记录“队列”中的元素个数。每次新来的元素都存在end指针所指向的位置。每次执行出队操作的时候，如果size的值不为零，则把start所指的元素弹出。利用size将start和end进行解耦

#include "pch.h"
#include
#include
using namespace std;

template
class MyQueue {
public:
	MyQueue(int i = 0, int j=0, int k=0);
	~MyQueue();

	void push(T input);
    const T pop();
	const T front ();
	const T back();
	const bool empty();

private:
	T *num;
	int start, end, size;
};

template inline
MyQueue::MyQueue(int i, int j, int k):
	start(i),end(j),size(k) {
	num = new T[3];
}

template inline
MyQueue::~MyQueue() {
	delete[] num;
}

template inline
void MyQueue::push(T input) {
	if (size == 3) {
		cout << "queue is full" << endl;
		return;
	}

	end = end == 3 ? 0 : end;
	num[end++] = input;
	size++;
}

template inline
const T MyQueue::pop() {
	if (size == 0) {
		cout << "queue is empty" << endl;
		return 0;
	}
	size--;
	start = start == 3 ? 0:start;
	return num[start++];
}

template inline 
const T MyQueue::front() {
	if (size == 0) {
		cout << "queue is empty" << endl;
		return 0;
	}
	return num[start];
}

template inline
const T MyQueue::back() {
	if (size == 0) {
		cout << "queue is empty" << endl;
		return 0;
	}
	int temp = end;
	return num[--temp];

}

template inline
const bool MyQueue::empty() {
	if (size == 0) return true;
	else return false;
}


int main()
{
	MyQueue queue;
	queue.push(1);
	queue.push(1);
	queue.push(1);
	queue.push(1);
	queue.pop();
	bool em=queue.empty();
	queue.push(2);
	int fr=queue.front();
	int bac=queue.back();
	queue.pop();
	queue.pop();
	queue.pop();
	queue.pop();
	queue.pop();

	return 0;
}

11、实现一个特殊的栈，在实现栈的基本功能的基础上，再实现返回栈中最小元素的操作。

要求：

1、pop、push、getMin造作的时间复杂度都是O(1)

2、设计的栈类型可以使用现成的栈结构。

思路：

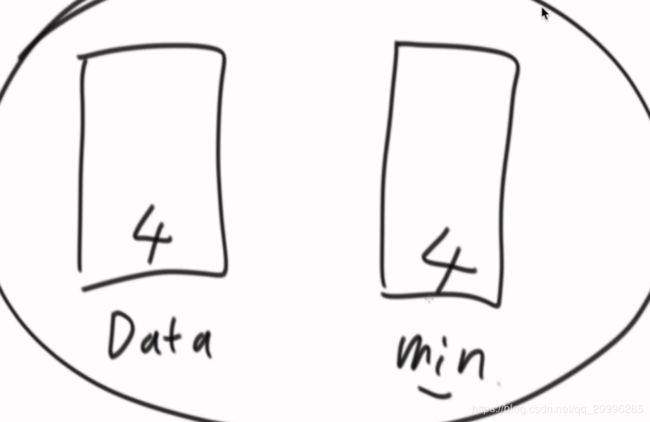
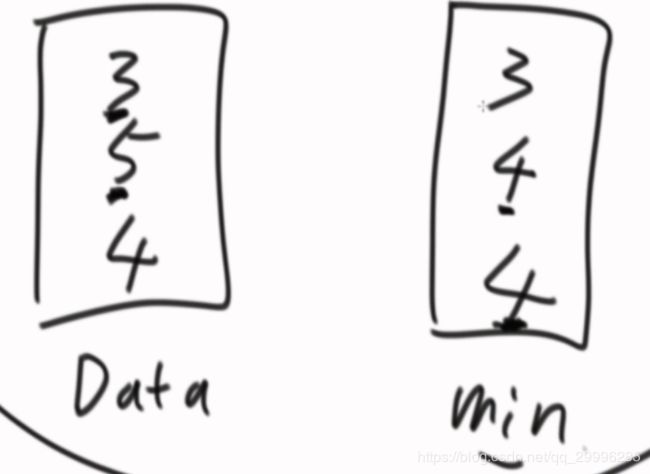
准备两个栈，一个存数据，一个存最小值，压入数据的时候，data栈和min栈一起增长：

一开始来一个数据四，则将4压入到两个栈中：

又来了一个数，这个数与栈顶元素进行比较，如果这个数比栈顶大，则重复压入栈顶元素，如果这个数比栈顶元素小，则将该值压入栈中。

/*
实现一个特殊的栈，在实现栈的基本功能的同时，再返回栈中最小元素的操作

一开始来一个数据，则将该数字压入到两个栈中：
又来了一个数，这个数与栈顶元素进行比较，如果这个数比栈顶大，则重复压入栈顶元素，
如果这个数比栈顶元素小，则将该值压入栈中
*/

#include "pch.h"
#include
#include
using namespace std;

class getMin {
public:
	int minNum();
	void push(int num);
	void pop();
private:
	stackmyStack, minStack;
};

inline 
void getMin::push(int num) {
	if (myStack.empty() && minStack.empty()) {
		myStack.push(num);
		minStack.push(num);
		return;
	}
	if (myStack.empty() || minStack.empty()) {
		cout << "push error" << endl;
		return;
	}
	else {
		if (num >= minStack.top()) {
			minStack.push(minStack.top());
		}
		else {
			minStack.push(num);
		}
		myStack.push(num);
	}
}

inline
void getMin::pop() {
	if (myStack.empty() && minStack.empty()) {
		cout << "stack is empty" << endl;
		return;
	}
	if (myStack.empty() && minStack.empty()) {
		cout << "pop error" << endl;
		return;
	}
	myStack.pop();
	minStack.pop();
}

inline
int getMin::minNum() {
	return minStack.top();
}

//产生随机数
int creatRadomNum() {
	return rand();
}

int main()
{
	getMin test;
	test.push(creatRadomNum());
	test.push(creatRadomNum());
	test.push(creatRadomNum());
	test.push(creatRadomNum());
	test.push(creatRadomNum());
	test.push(creatRadomNum());
	int a=test.minNum();
	test.pop();
	int b = test.minNum();
	test.pop();
	int c = test.minNum();
	test.pop();
	int d = test.minNum();
	test.pop();
	int e = test.minNum();
	system("pause");
	return 0;
}

12、栈实现队列，用队列实现栈

栈实现队列

两个栈，push和pop，入队操作的时候，永远都向push栈压入元素，出队操作的时候，永远都从pop栈弹出元素。

原则：

1、push栈向pop栈倒数据，一定要把push栈倒空；

2、如果pop栈非空，则不允许push栈向pop栈倒数据；

class MyQueue {
private:
	stackpushStack, popStack;
public:
	void push(int num);
	void pop();
	int peak();
	bool empty();
};

void MyQueue::push(int num) {
	pushStack.push(num);
}

void MyQueue::pop() {
	if (popStack.empty()) {
		if (pushStack.empty()) {
			cout << "queue is empty" << endl;
			return;
		}
		while (!pushStack.empty()) {
			popStack.push(pushStack.top());
			pushStack.pop();
		}
	}
	popStack.pop();
}

int MyQueue::peak() {
	if (popStack.empty()) {
		if (pushStack.empty()) {
			cout << "queue is empty" << endl;
			return;
		}
		while (!pushStack.empty()) {
			popStack.push(pushStack.top());
			pushStack.pop();
		}
	}
	return popStack.top();
}

bool MyQueue::empty() {
	if (pushStack.empty() && popStack.empty()) return true;
	else return false;
}

队列实现栈

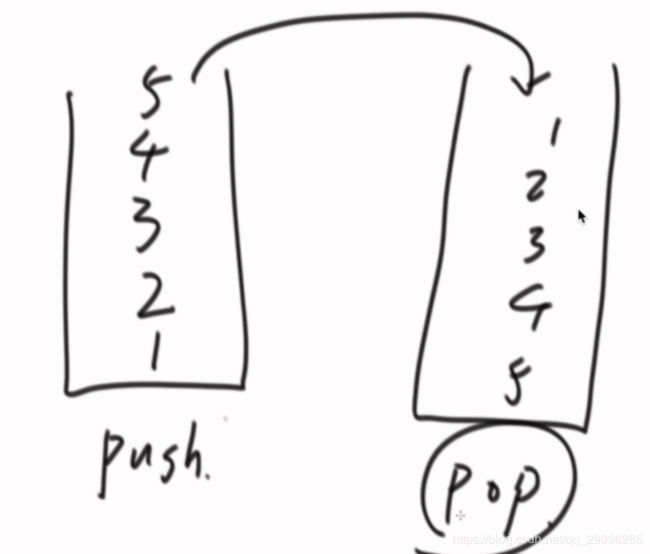
两个队列，入栈操作的时候只在一个队列中加入数据；出栈操作的时候，将数据依次弹出并加入到另一个队列中，当弹出元素为队尾元素时，将该值返回给用户，不将该值压入到另一个队列中。

class MyStack {
private:
	queuedata, help;
public:
	/** Initialize your data structure here. */
	MyStack() { }

	/** Push element x onto stack. */
	void push(int x) {
		if (data.empty() && help.empty()) {
			data.push(x);
			return;		
		}
		else if (data.empty()) {
			help.push(x);
		}
		else {
			data.push(x);
		}
	}
	
	void helper(queue&output, queue&input) {
		while (output.size() != 1) {
			input.push(output.front());
			output.pop();
		}
	}

	/** Removes the element on top of the stack and returns that element. */
	int pop() {
		if (data.empty() && help.empty()) return 0;
		else if (data.empty()) {
			//把另一个队列里面的元素放入data队列中，将help队列中的队尾返回
			helper(help,data);
			int answer = help.front();
			help.pop();
			return answer;
		}
		else {
			helper(data,help);
			int answer = data.front();
			data.pop();
			return answer;
		}
	}

	/** Get the top element. */
	int top() {
		int answer = 0;
		if (data.empty() && help.empty()) return answer;
		else if (data.empty()) {
			//把另一个队列里面的元素放入data队列中，将help队列中的队尾返回
			helper(help, data);
			answer = help.front();
			data.push(answer);
			help.pop();
		}
		else {
			helper(data, help);
			answer = data.front();
			help.push(answer);
			data.pop();
		}
		return answer;
	}

	/** Returns whether the stack is empty. */
	bool empty() {
		if (data.empty() && help.empty()) return true;
		else return false;
	}
};

码力十足！

左神初级班 （一）