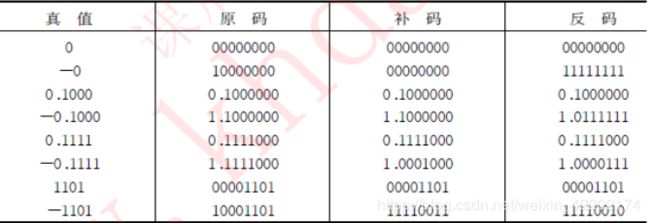
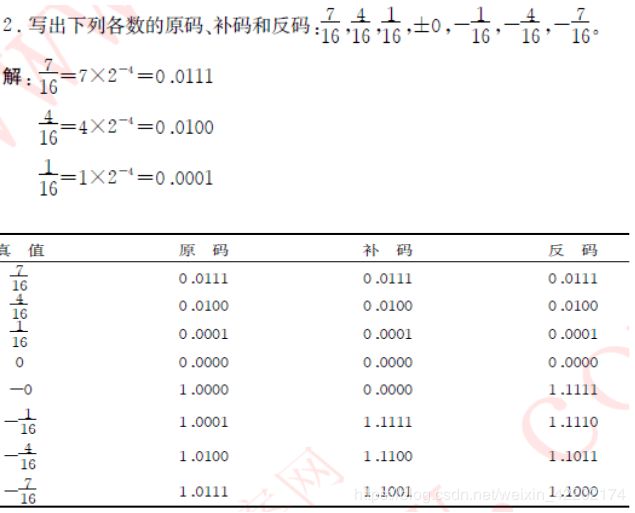
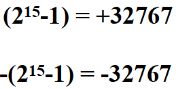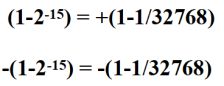第二章 数据的机器层次表示习题

1、下列数中最小的数是（ C ）。

A （101001）2   2的0次方+2的3次方+2的5次方=41

B （52）8        2*8的0次方+5*8的一次方=42

C （101001）BCD       = 29

bcd码从头取4位即1001(2)，表示9，即个位数是9，剩余两位是10(2)，表示2，即十位数是2，转换为10进制即为29

D （233）16    转换为二进制为001000110011

2、将十进制数215.6531转换成二进制数是（ C  ）。

    A. 11110010.000111      B.11101101.110011

C.11010111.101001          D.11100001.111101

215=

3、二进制整数采用机器码表示时，（ B）的表示范围最大。

    A. 原码    B. 补码    C. 反码      D. BCD码

4、8位定点原码整数10100011B的真值为（ B）。

   A.+0100011B         B.-0100011B      

   C.+1011101B         D.-1011101B

5、在（ C）表示中，数值0是唯一表示的。

  A．原码   B．反码    C．补码    D．原码或反码

    解析： 在对数值的两种编码中，数值0，若用8位二进制编码表示，可用原码00000000或10000000来表示。若用反码表示，则可表示为00000000或11111111。用补码表示，则只能用00000000来表示。而用移码表示，则唯一的数值是10000000。故为C。

6、若某数X的真值为-0.1010，在计算机中该数表示为1.0110，则该数所用的编码为（   ）。B       [X]原=1.1010  [X]反=1.0101  [X]补=1.0110

    A.原码        B.补码          C.反码           D.移码

7、已知X的补码为10011001，其原码是_________，真值为 _______。11100111、－103

 

8、FFH代表无符号数时等价的十进制值为          ，代表补码有符号数时等价的十进制值为        ，代表反码有符号数时等价的十进制值为        ，代表原码有符号数时等价的十进制值为       。255、-1、-0、-127

FFH：无符号时的二进制为11111111=2的0次方+......+2的7次方=255

FFH：有符号时的补码二进制为11111111，[X]原=10000001    [X]反=11111110     [X]补=11111111   x真值为-00000001 对应的十进制为-1

FFH：代表反码时的有符号数   [X]反=11111111  [X]原=10000000   x真值为-0000000

FFH:  代表原码时的有符号数   [X]原=11111111  x真值为-1111111   -127

-128没有对应的原码和反码

设机器字长16位，定点表示，尾数15位，数符1位，问：
 (1)定点原码整数表示时，最大正数是多少？最小负数是多少？
 (2)定点原码小数表示时，最大正数是多少？最小负数是多少？

定点原码整数

定点原码小数

 

 

（考点）例题

将(100.25)10转换成短浮点数格式。

解: (1)把十进制数转换成二进制数

       (100.25)10 ＝(1100100.01)2

    (2)规格化二进制数      

       1100 100.01＝1.1001 0001×26   （右规6位）

    (3)计算阶码的移码（偏置值＋阶码真值）

       1111111(127)＋110 ＝1000 0101

    注意：短浮点数的阶码偏置值是1111111(127)。

    (4)以短浮点数格式存储该数

     该数的符号位＝0   ,

         阶码＝1000 0101

         尾数＝10010001000000000000000 （23位，隐含最高位1）

     所以(100.25)10的短浮点数代码为

      0；1000 0101；10010001000000000000000

     十六进制值是42C88000H。

 

例2.将短浮点数C1C90000H转换成十进制数。

解:（1）把十六进制数转换成二进制形式，并分离出符号位、阶码和尾数。

因为，C1C90000H＝1 10000011 10010010000000000000000B

   所以，符号位＝1

             阶码＝10000011 (8位)

                     尾数＝10010010000000000000000(23位)

   （2）计算出阶码的真值（即移码-偏置值）

         10000011 -1111111＝100

   （3）以规格化二进制数形式写出此数

         1.1001001×24 （尾数部分加上隐含的1）

   （4）写成非规格化二进制数形式

         11001．001

   （5）转换成十进制数，并加上符号位

         （-11001.001）2＝（-25.125）10

例3.将十进制数-0.625转换为IEEE短浮点数。

解: （1）把十进制数转换成二进制数

          (-0.625)10 ＝(-0.101)2

    （2）规格化二进制数      

           -1.01×2-1

     (3)计算阶码的移码（偏置值＋阶码真值）

       1111111(127)-001＝0111 1110

    注意：短浮点数的阶码偏置值是1111111(127)。

    (4)以短浮点数格式存储该数

     该数的符号位＝1   ,

         阶码＝01111 1110

         尾数＝01000000000000000000000

                          （23位，隐含最高位1）

     所以-0.625 的短浮点数代码为

      1；0111 1110；01000000000000000000000

     十六进制值是BF200000H。   

浮点数小结：

1.规格化：原码和补码不同

2.对于IEEE 754的规格化的二进制浮点数，数值最高位为1，为了能使尾数多1位有效位，可将这个1隐含。

 

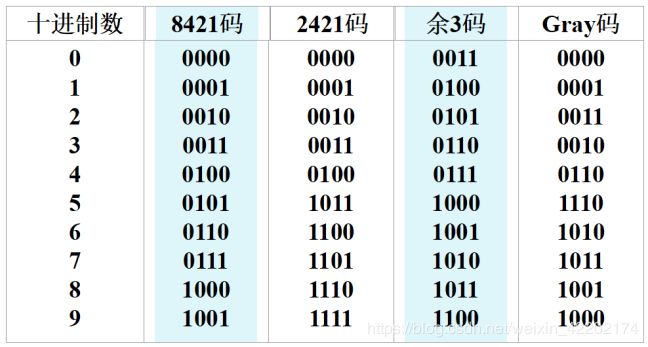
BCD码：用四位二进制数来表示一位十进制数，称为二进制编码的十进制数，简称BCD码。

BCD编码既具有二进制数的形式，又保持了十进制数的特点。

几种常见的BCD码

 

习题：

1. (2011)float型数据通常用IEEE754单精度浮点数格式表示。若编译器将float型变量x分配在一个32位浮点寄存器FR1中，且x= -8.25，则FR1的内容是(  A   )

     (A)C104 0000H                                 (B) C242 0000H        

     (C) C184 0000H                                (D) C1C2 0000H

2. (2013)某数采用IEEE 754单精度浮点数格式表示为C640 0000H，则该数的值是(   A    )

   (A)-1.5×213                               (B) -1.5×212          

   (C) -0.5x×213                            (D) -0.5×212

 

一、填空题

1、按小数点位置不同，定点数有（ 原码定点小数 ）和（补码定点小数  ）两种表示方法。

原码定点小数表示范围为：-(1-2-n)～(1-2-n)

补码定点小数表示范围为：-1～(1-2-n)

整数原码表示范围为：-（2n -1）≤x ≤ 2n -1

整数补码表示范围为：- 2n ≤x ≤ 2n -1

2、数的真值变成机器码时有三种表示方法，即（原码  、反码  、补码 ）。

3、所有信息在计算机中都是以（二进制）编码的形式存在的。英文符号的编码占用一个（字节　）的空间；汉字编码占用（两）个字节的空间；

4、ASCII码中，英文字母按顺序排列，且大写字母在前，小写字母在后；已知‘Ａ’的ASCII码为41H，问‘Ｆ’的ASCII码是（）；’A’=65   

‘Ｆ’的二进制码为0100 0110 十进制为70  十六进制为46H

5、浮点数的取值范围由阶码的位数决定，而精度由尾数的（  位数 ）决定。

6、BCD码中，每一位十进制数字由（ 4 ）位二进制数码组成。

二、选择题

1、 32个汉字的机内码需要是( C )字节。

    A.16     B.32        C.64     D.128

2、已知汉字“春”的国标码为343AH，其机内码为（　C ）
  Ａ.8080H　 Ｂ.B4BAH　  Ｃ.343AH　  Ｄ.A4AAH

 国标码＝区位码（十六进制）＋2020H

已知汉字“春”的区位码为“20-26”，

3、计算机中的数有浮点与定点数两种，其中用浮点数表示的数，通常由（　C ）两部分组成
  Ａ.指数与基数          Ｂ.尾数与小数　

    Ｃ.阶码与尾数　       Ｄ.整数与小数

三、计算题

1、请比较有符号数补码321FH和A521H的大小。

 

2、分别写出下列真值的原码、反码和补码
-0.101101   +0.101101

 

3、 将下列十进制数转换成相应的二进制数。

     （57．687）10=（              ）2

 

4、将下列二进制数转换成相应的十进制数、八进制数、 十六进制数。   （10100.1011）2

5、将十进制数+13/128写成二进制定点数和浮点数（数值部分取10位，阶码部分取4位，阶符和数符各取1位），分别写出它在定点机和浮点机中的机器数形式。

　解：令x = +13/128

　　其二进制形式：x = 0.0001101000 （纯小数数值部分取10位）

　　定点数形式：x = 0.0001101000

　　浮点数规格化表示：x = 0.1101000000×2-0011

　　定点机中[x]原=[x]补=[x]反=0.0001101000

　　浮点机中[x]原 = 1, 0011 ; 0.1101000000

            [x]补 = 1, 1101 ; 0.1101000000