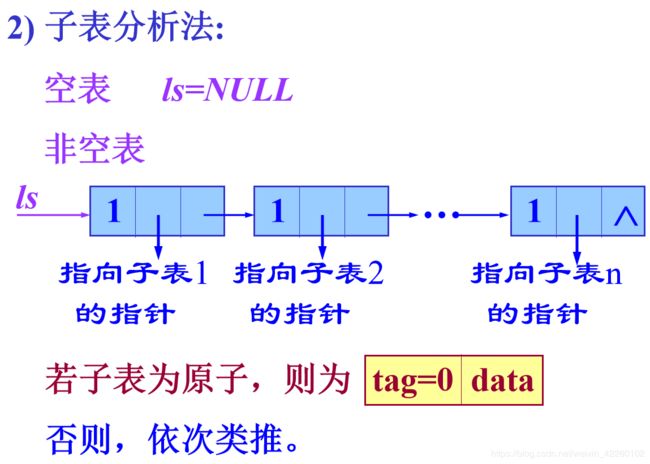
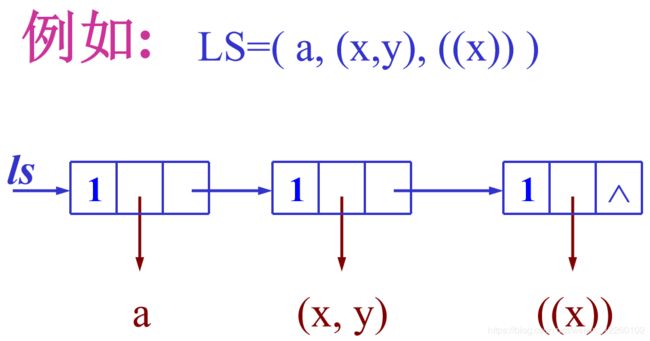
数据结构第五章:数组和广义表
之前的线性结构的数据构成特点:
- 线性表的数据构成:原子类型数据对象
- 栈和队列的数据构成:原子类型的数据对象
- 串的数据构成:字符
实际上,线性结构可以包含更广泛的数据类型:
- 可以是原子类型的数据对象;
- 可以是结构类型的数据对象;
- 可以是混合类型的数据—广义表
1 数组的类型定义
1.一维数组
一维数组可看成是一个线性表或一个向量,存储在一块连续的存储单元中,适合于随机查找。一维数组记为A[n]或A=(a0,al,…ai,…,an-1) ,一维数组中ai的存储地址LOC(ai)可由下式求出:
LOC(ai)=LOC(a0)+i*L (0≤i
2.二维数组
二维数组,又称矩阵(matrix)。每个元素又是一个定长的线性表(一维数组),都要受到两个关系即行关系和列关系的约束,也就是每个元素都同属于两个线性表。例如,设A是一个有m行n列的二维数组,A可以看成由m个行向量组成的向量,也可以看由n个列向量组成的向量。

一个二维数组可以看作是每个数据元素类型相都同的一维数组。以此类推,任何多维数组都可以看作一个线性表,这时线性表中的每个数据元素也是一个线性表。多维数组是特殊的线性表,是线性表的推广。
数组的性质:
(1) 数组中数据元素数目固定。一旦定义了一个数组,其数据元素数目不再有增减变化,属于静态分配存储空间的数据结构。
(2) 数组中数据元素必须具有相同的数据类型。
(3) 数组中每个数据元素都有一组唯一的下标值。
(4)数组是一种随机存取结构,可随机存取数组中的任意数据元素。
(5)对于数组的操作一般只有两类:获得特定位置的元素值和修改特定位置的元素值。



2 数组的顺序表示和实现
数组的特点:
1)只有引用型操作,没有加工型操作;
2)数组是多维结构,存储空间是一维结构。
两种顺序映象方式:
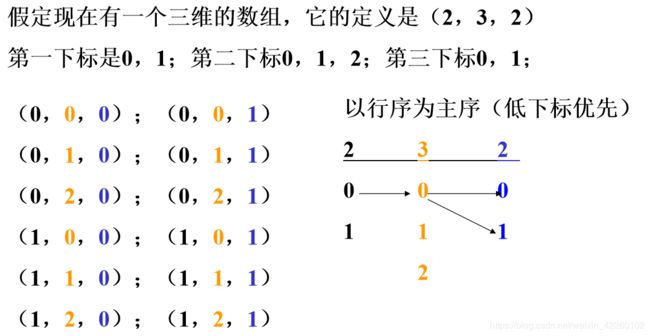
1)以行序为主序(低下标优先);
2)以列序为主序(高下标优先);
以“行序为主序”的存储映象
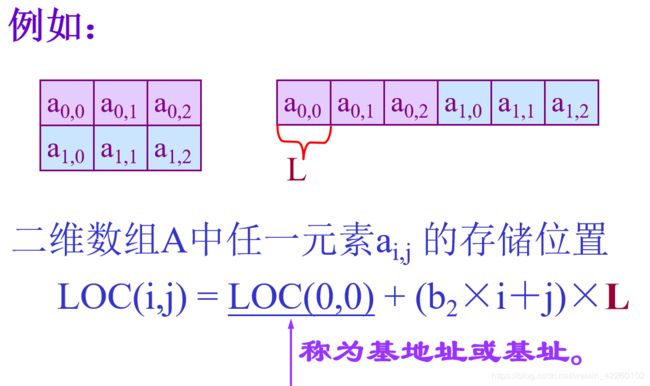
“行序为主序” 即 “低下标优先”


【例5-1】对于给定的二维数组float a[ 3 ][ 4 ],计算:
(1) 数组a中的数组元素数目;
(2)若数组a的起始地址为1000,且每个数组元素长度为32位(即4个字节),数组元素a[2][3]的内存地址。
【解】(1)由于C语言中数组的行、列下标值的下界均为0,该数组行上界为3-1=2,列上界为4-1=3,所以该数组的元素数目共有34=12个。
(2)由于C语言采用行序为主序的存储方式,有:
LOC(a2,3)=LOC(a0,0)+(in+j)k
=1000+(24+3)*4
=1044

按上述两种方式顺序存储的数组,只要知道开始结点的存放地址(即基地址),维数和每维的上、下界,以及每个数组元素所占用的单元数,就可以将数组元素的存放地址表示为其下标的线性函数。因此,数组中的任一元素可以在相同的时间内存取,即顺序存储的数组是一个随机存取结构。
数据类型描述
typedef int ElemType;
typedef struct {
ElemType *base;//数组元素基址
int dim;//数组维数
int *bounds;//数组维长
int *constants;//常数因子
}Array;
//初始化数组
Status InitArray(Array *A, int dim, ...){
if (dim<1||dim>MAX_ARRAY_DIM)
{
return ERROR;
}
A->dim = dim;
A->bounds = (int *)malloc(dim*sizeof(int));
int elemtotal = 1;
va_list ap;
va_start(ap, dim);
for (int i = 0; i < dim; i++)
{
A->bounds[i] = va_arg(ap, int);
elemtotal *= A->bounds[i];
}
va_end(ap);
A->base = (int *)malloc(sizeof(int)*elemtotal);
A->constants = (int *)malloc(dim*sizeof(int));
A->constants[dim - 1] = 1;
for (int i = dim-2; i >= 0; i--)
{
A->constants[i] = A->constants[i + 1] * A->constants[i + 1];
}
return OK;
}
//销毁数组
Status Destory(Array *A){
if (!A->base)
{
return OK;
}
free(A->base);
A->base = NULL;
if (!A->bounds)
{
return OK;
}
free(A->bounds);
A->bounds = NULL;
if (!A->constants)
{
return OK;
}
free(A->constants);
A->constants = NULL;
}
//元素定位
bool Locate(Array *A, va_list ap, int *off){
*off = 0;
for (int i = 0; i < A->dim; i++)
{
int ind = va_arg(ap, int);
if (ind<0||ind>A->bounds[i])
{
return false;
}
(*off) += A->constants[i] * ind;
}
}
//若下标不越界,则将e赋值为指定的A的元素
void Value(Array *A, int *e, ...){
va_list ap;
va_start(ap, e);
int off;
if (!Locate(A,ap,&off))
{
return;
}
*e = *(A->base + off);
}
3 稀疏矩阵的压缩存储
假设m行n列的矩阵含t个非零元素,则称 δ = t m ∗ n \delta =\frac{t}{m*n} δ=m∗nt为稀疏因子,通常认为 δ ≤ 0.05 \delta \leq 0.05 δ≤0.05的矩阵为稀疏矩阵。
以常规方法,即以二维数组表示高阶稀疏矩阵时产生的问题:
1)零值元素占的空间很大;
2)计算中进行了很多和零值的运算。
解决问题的原则:
1)尽可能少存或不存零值元素;
2)尽可能减少没有实际意义的运算;
3)运算方便,即:
能尽可能快地找到与下标值(i,j)对应的元素;
能尽可能快地找到同一行或同一列的非零值元。
有两类稀疏矩阵:
- 特殊矩阵:非零元在矩阵中的分布有一定规则
例如: 三角矩阵,对角矩阵 - 随机稀疏矩阵:非零元在矩阵中随机出现
3.1 特殊矩阵
三角矩阵大体分为三类:下三角矩阵、上三角矩阵和对称矩阵。
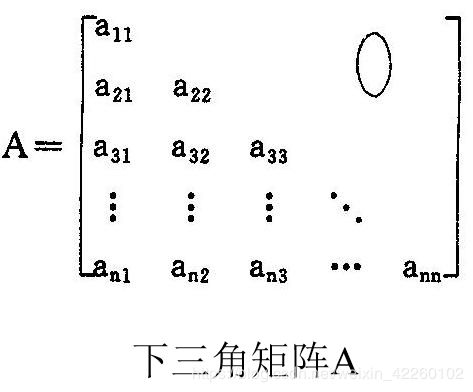
对下三角矩阵只存储下三角的非零元素,对于零元素则不存。按“行序为主序”进行存储,得到的序列是a11, a21, a22, a31, a32, a33, …, an1, an2, …, ann。由于下三角矩阵的元素个数为n(n+1)/2,即:
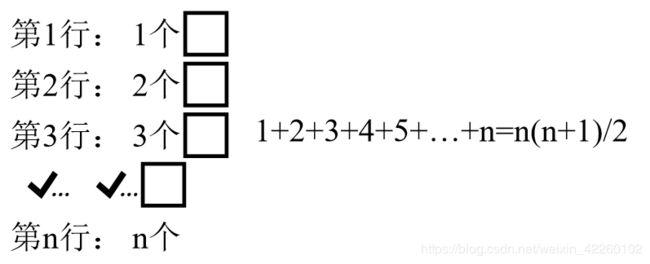
所以可压缩存储到一个大小为n(n+1)/2的一维数组C中,如下图所示。
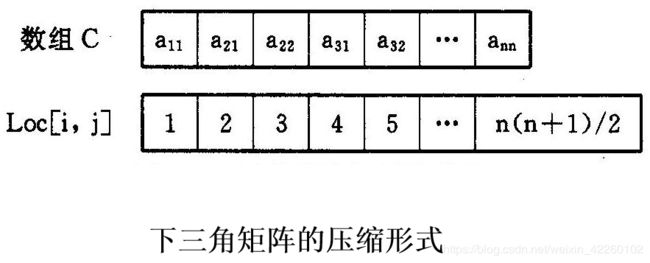
下三角矩阵中元素aij(i>j)在一维数组A(存储器中)中的位置为:
Loc[i,j]=Loc[1,1]+前i-1行非零元素个数+第i行中aij前非零元素个数;
前i-1行元素个数=1+2+3+4+…+(i-1)=i(i-1)/2;第i行中aij前非零元素个数=j-1;
所以有Loc[i,j]=Loc[1,1]+i(i-1)/2+j-1
同样,对于上三角矩阵,也可以将其压缩存储到一个大小为n(n+1)/2的一维数组C中。其中元素aij(i
对于对称矩阵,因其元素满足aij=aji,可以为每一对相等的元素分配一个存储空间,即只存下三角(或上三角)矩阵,从而将n2个元素压缩到n(n+1)/2个空间中。
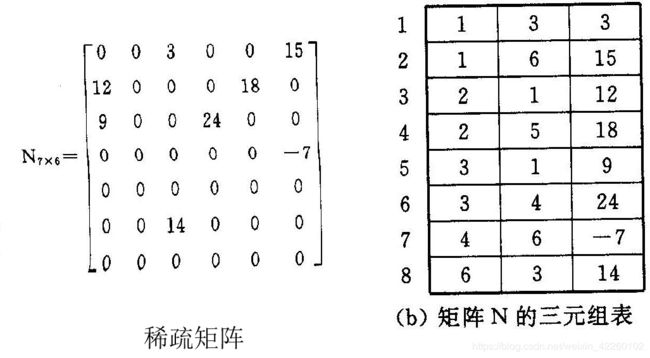
3.2随机稀疏矩阵的压缩存储方法
-
三元组顺序表
//三元组顺序表稀疏矩阵 #include#define MAXSIZE 12500 #define ElemType int typedef struct{ int i, j;//该非零元的行下标和列下标 ElemType e;// 该非零元的值 }Triple;// 三元组类型 typedef union{ Triple data[MAXSIZE + 1]; int mu, nu, tu; }TSMatrix;//稀疏矩阵类型 for (col=1; col<=nu; ++col) for (row=1; row<=mu; ++row) T[col][row] = M[row][col];其时间复杂度为: O(mu×nu)
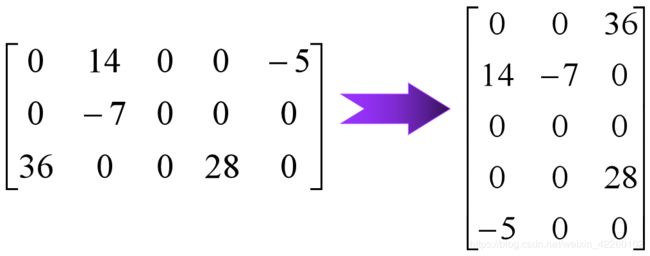
用“三元组”表示时如何实现?

首先应该确定转置矩阵中每一列的第一个非零元在三元组中的位置。

cpot[1] = 1; for(col=2; col<=M.nu; ++col) cpot[col] = cpot[col-1] + num[col-1];Status FastTransposeSMatrix(TSMatrix M, TSMatrix &T){ T.mu = M.nu; T.nu = M.mu; T.tu = M.tu; if (T.tu) { for(col=1; col<=M.nu; ++col) num[col] = 0; for(t=1; t<=M.tu; ++t) ++num[M.data[t].j]; cpot[1] = 1; for(col=2; col<=M.nu; ++col) cpot[col] = cpot[col-1] + num[col-1]; for(p=1; p<=M.tu; ++p) { col = M.data[p].j; q = cpot[col]; T.data[q].i = M.data[p].j; T.data[q].j = M.data[p].i; T.data[q].e = M.data[p].e; ++cpot[col]; } } // if return OK; } // FastTransposeSMatrix -
行逻辑联接的顺序表
三元组顺序表又称有序的双下标法,它的特点是非零元在表中按行序有序存储,因此便于进行依行顺序处理的矩阵运算。然而,若需随机存取某一行中的非零元,则需从头开始进行查找。
修改前述的稀疏矩阵的结构定义,增加一个数据成员rpos,其值在稀疏矩阵的初始化函数中确定。#define MAXMN 500 typedef struct { Triple data[MAXSIZE + 1]; int rpos[MAXMN + 1]; int mu, nu, tu; } RLSMatrix; // 行逻辑链接顺序表类型例如:给定一组下标,求矩阵的元素值
ElemType value(RLSMatrix M, int r, int c){ int p; p = M.rpos[r]; while (M.data[p].i==r&&M.data[p].j<c) { p++; } if (M.data[p].i==r&&M.data[p].j==c) { return M.data[p].e; } else { return 0; } }两个稀疏矩阵相乘(Q=M×N)的过程可大致描述如下:
Q初始化; if Q是非零矩阵 { // 逐行求积 for (arow=1; arow<=M.mu; ++arow) { // 处理M的每一行 ctemp[] = 0; // 累加器清零 计算Q中第arow行的积并存入ctemp[] 中; 将ctemp[] 中非零元压缩存储到Q.data; } // for arow } // if//稀疏矩阵相乘 int MultSMatrix(RLSMatrix M, RLSMatrix N, RLSMatrix *Q){ int i, tp, p, q, arow, brow, ccol, ctemp[MAXMN]; if (M.nu!=M.mu) { return ERROR; } Q->mu = M.mu; Q->nu = N.nu; Q->tu = 0; if (M.tu*N.tu==0) { return ERROR; } else { for (arow = 1; arow <= M.mu; arow++) { for (i = 1; i <=M.nu ; i++) { ctemp[i] = 0; } Q->rpos[arow] = Q->tu + 1; if (arow<M.mu) { tp = M.rpos[arow + 1]; } else { tp = M.tu + 1; } for (p = M.rpos[arow]; p < tp; p++) { brow = M.data[p].j; int t; if (brow<M.mu) { t = N.rpos[brow] + 1; } else { t = N.tu + 1; } for (q = N.rpos[brow]; q < t; q++) { ccol = N.data[q].j; ctemp[ccol] += M.data[p].e*N.data[q].e; } } for (ccol = 1; ccol <= Q->nu; ++ccol) { if (ctemp[ccol]) { if (++Q->tu > MAXSIZE)return ERROR; Q->data[Q->tu].i = arow; Q->data[Q->tu].j = ccol; Q->data[Q->tu].e = ctemp[ccol]; } } } } return OK; } -
十字链表
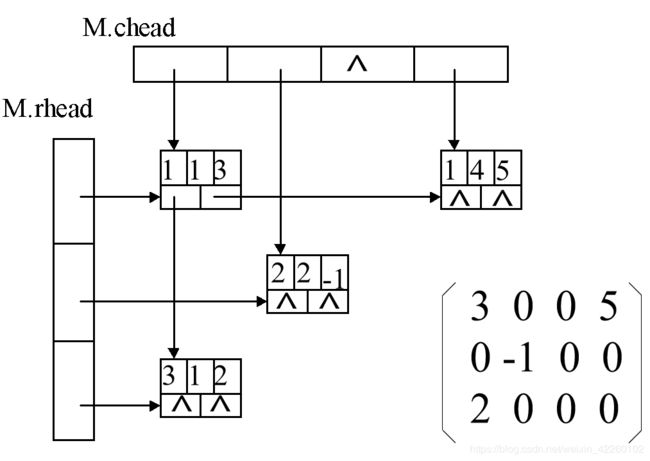
用三元数组的结构来表示稀疏矩阵,在某些情况下可以节省存储空间并加快运算速度。但在运算过程中,若稀疏矩阵的非零元素位置发生变化,必将会引起数组中元素的频繁移动。这时,采用链式存储结构(十字链表)表示三元组的线性表更为恰当。十字链表(orthogonal list)用多重链表来存储稀疏矩阵。十字链表适用于操作过程中非零元素的个数及元素位置变动频繁的稀疏矩阵。
十字链表为矩阵中的每一行设置一个单独链表,同时也为每一列设置一个单独链表。这样,矩阵中的每个非零元就同时包含在两个链表中(即所在行和所在列的链表)。这就大大降低了链表的长度,方便了算法中行方向和列方向的搜索,大大降低了算法的时间复杂度。
对于一个m×n的稀疏矩阵,每个非零元用一个含有五个域的结点来表示。其中各分量含义如下:
(1) 矩阵中非零元素的行号i;
(2) 矩阵中非零元素的列号j;
(3) 矩阵中非零元素的值value;
(4) 向右域right,用以链接同一行中下一个非零元素;
(5) 向下域down,用以链接同一列中下一个非零元素。
同一行的非零元素通过right域链接成一个链表,同一列的非零元素通过down域链接成一个链表,每一个非零元既是某个行链表中的结点,同时又是某个列链表中的结点。整个矩阵构成了一个十字交叉的链表。
4 广义表的定义
一个广义表是n(n≥0)个元素的一个序列,若n=0时则称为空表。设ai为广义表的第i个元素,则广义表的一般表示与线性表相同:
GL=(a1,a2,…,ai,…,an)
其中n表示广义表的长度,n≥0。如果ai是单个数据元素,则ai是广义表的原子;如果ai是一个广义表,则ai是广义表的子表。
广义表的类型定义


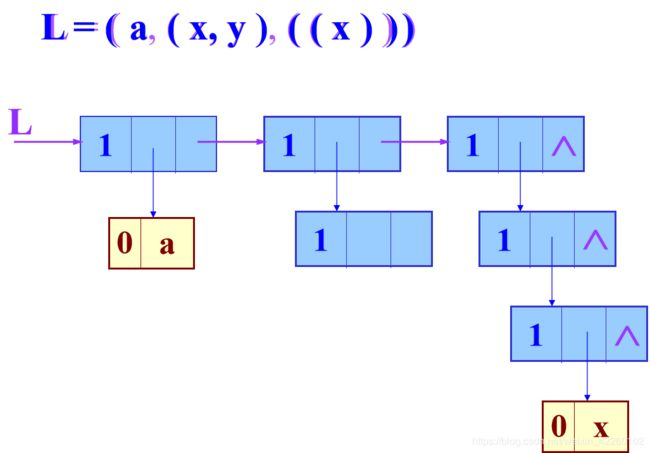
广义表是递归定义的线性结构

广义表是一个多层次的线性结构

广义表的分类
(1)线性表:元素全部是原子的广义表。
(2)纯表:与树对应的广义表。
(3)再入表:与图对应的广义表(允许结点共享),
(4)递归表:允许有递归关系的广义表,例如E=(a,E)。
这四种表的关系满足:递归表>再入表> 纯表 > 线性表

广义表 L S = ( α 1 , α 2 , . . . , α n ) LS=(\alpha _{1},\alpha _{2},...,\alpha _{n}) LS=(α1,α2,...,αn)的结构特点:
- 广义表中的数据元素有相对次序;
- 广义表的长度定义为最外层包含元素个数;
- 广义表的深度定义为所含括弧的重数;
注意:“原子”的深度为 0 ;
“空表”的深度为 1 。 - 广义表可以共享;
- 广义表可以是一个递归的表;
递归表的深度是无穷值,长度是有限值。 - 任何一个非空广义表 L S = ( α 1 , α 2 , . . . , α n ) LS=(\alpha _{1},\alpha _{2},...,\alpha _{n}) LS=(α1,α2,...,αn)均可分解为
表头 Head(LS) = α 1 \alpha _{1} α1 和
表尾 Tail(LS) = ( α 2 , . . . , α n ) (\alpha _{2},...,\alpha _{n}) (α2,...,αn)两部分

为简单起见,下面讨论的广义表不包括再入表和递归表,即只讨论一般的广义表。另外,规定用小写字母表示原子,用大写字母表示广义表的表名。例如:
A=()
B=(e)
C=(a,(b,c,d))
D=(A,B,C)=((),(e),(a,(b,c,d)))
E=((a,(a,b),((a,b),c)))
如果把每个表的名字(若有的话)写在其表的前面,则上面的5个广义表可相应地表示如下:
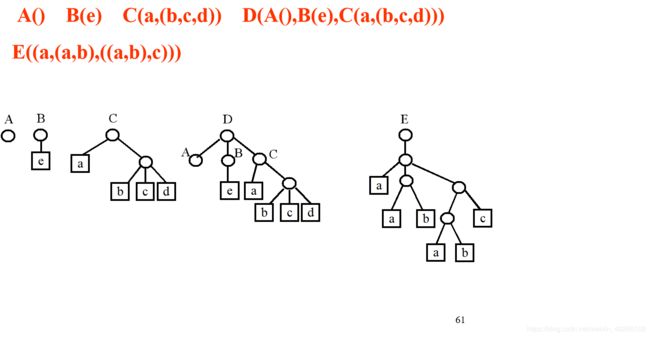
A()
B(e)
C(a,(b,c,d))
D(A(),B(e),C(a,(b,c,d)))
E((a,(a,b),((a,b),c)))
若用圆圈和方框分别表示表和单元素,并用线段把表和它的元素(元素结点应在其表结点的下方)连接起来,则可得到一个广义表的图形表示。例如,上面五个广义表的图形表示如下图所示。