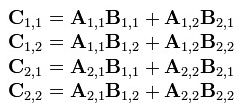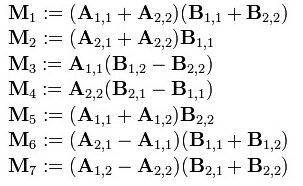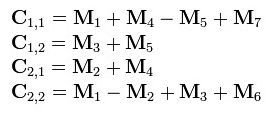1 题目描述
2 思路分析
3 解法
4 小结
1 题目描述
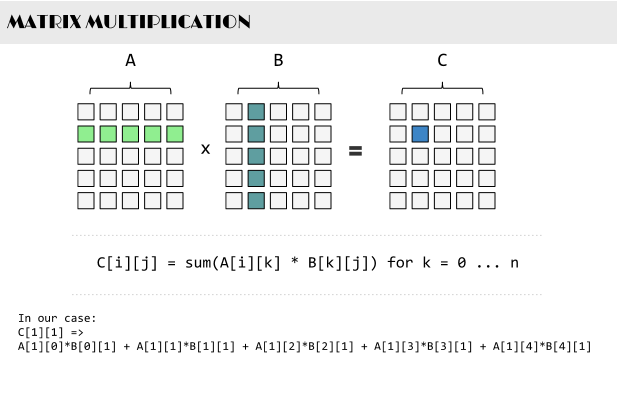
请编程实现矩阵乘法,并考虑当矩阵规模较大时的优化方法。
2 思路分析
根据wikipedia上的介绍:两个矩阵的乘法仅当第一个矩阵B的列数和另一个矩阵A的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵,它们的乘积AB是一个m×p矩阵,它的一个元素其中 1 ≤ i ≤ m, 1 ≤ j ≤ p。
值得一提的是,矩阵乘法满足结合律和分配率,但并不满足交换律,如下图所示的这个例子,两个矩阵交换相乘后,结果变了:
3 解法
解法一、暴力解法
根据矩阵的性质,通过三个for循环,即可完成计算。其实,通过前面的分析,我们已经很明显的看出,两个具有相同维数的矩阵相乘,其复杂度为O(n^3)
//方法1:暴力解
//根据矩阵的性质i*j=i*n+n*j直接计算
public static void directCal(){
int [][]matrix1 = {{1,2},{3,4}};
int [][]matrix2 = {{4,5},{6,7}};
int [][]matrix3 = {{0,0},{0,0}};
int n = matrix1.length;
//计算
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
matrix3[i][j] = 0;
for (int k = 0; k < n; k++) {
matrix3[i][j]+= matrix1[i][k]*matrix2[k][j];
}
}
}
//输出结果
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(matrix3[i][j]+" ");
}
System.out.println();
}
}
解法二、Strassen算法
在解法一中,我们用了3个for循环搞定矩阵乘法,但当两个矩阵的维度变得很大时,O(n^3)的时间复杂度将会变得很大,于是,我们需要找到一种更优的解法。
一般说来,当数据量较大时,我们往往会把大的数据分割成小的数据,各个分别处理。遵此思路,如果给我们一个很大的两个矩阵呢,是否可以考虑分治的方法循序渐进处理各个小矩阵的相乘,因为我们知道一个矩阵是可以分成更多小的矩阵的。
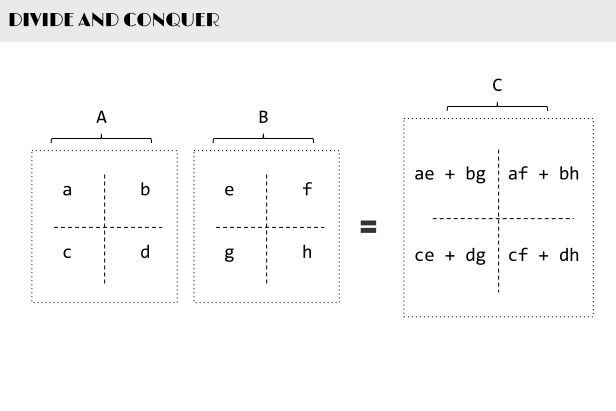
如下图,当给定一个两个二维矩阵A B时:
这两个矩阵A B相乘时,我们发现在相乘的过程中,有8次乘法运算,4次加法运算:
矩阵乘法的复杂度主要就是体现在相乘上,而多一两次的加法并不会让复杂度上升太多。故此,我们思考,是否可以让矩阵乘法的运算过程中乘法的运算次数减少,从而达到降低矩阵乘法的复杂度呢?答案是肯定的。
1969年,德国的一位数学家Strassen证明O(N3)的解法并不是矩阵乘法的最优算法,他做了一系列工作使得最终的时间复杂度降低到了O(n2.80)。
他是怎么做到的呢?还是用上文A B两个矩阵相乘的例子,他定义了7个变量:
如此,Strassen算法的流程如下:
-
1 两个矩阵A B相乘时,将A, B, C分成相等大小的方块矩阵:
可以看出C是这么得来的:
现在定义7个新矩阵(读者可以思考下,这7个新矩阵是如何想到的):
而最后的结果矩阵C 可以通过组合上述7个新矩阵得到:
表面上看,Strassen算法仅仅比通用矩阵相乘算法好一点,因为通用矩阵相乘算法时间复杂度是
而Strassen算法复杂度只是
但随着n的变大,比如当n >> 100时,Strassen算法是比通用矩阵相乘算法变得更有效率。
实验结果:
数据取600位上界,即超过10分钟跳出。可以看到使用Strassen算法时,耗时不但没有减少,反而剧烈增多,在n=700时计算时间就无法忍受。仔细研究后发现,采用Strassen算法作递归运算,需要创建大量的动态二维数组,其中分配堆内存空间将占用大量计算时间,从而掩盖了Strassen算法的优势。于是对Strassen算法做出改进,设定一个界限。当n<界限时,使用普通法计算矩阵,而不继续分治递归。
改进后算法优势明显,就算时间大幅下降。之后,针对不同大小的界限进行试验。在初步试验中发现,当数据规模小于1000时,下界S法的差别不大,规模大于1000以后,n取值越大,消耗时间下降。最优的界限值在32~128之间。
因为计算机每次运算时的系统环境不同(CPU占用、内存占用等),所以计算出的时间会有一定浮动。虽然这样,试验结果已经能得出结论Strassen算法比常规法优势明显。使用下界法改进后,在分治效率和动态分配内存间取舍,针对不同的数据规模稍加试验可以得到一个最优的界限。
4 小结:
1)采用Strassen算法作递归运算,需要创建大量的动态二维数组,其中分配堆内存空间将占用大量计算时间,从而掩盖了Strassen算法的优势
2)于是对Strassen算法做出改进,设定一个界限。当n<界限时,使用普通法计算矩阵,而不继续分治递归。需要合理设置界限,不同环境(硬件配置)下界限不同
3)矩阵乘法一般意义上还是选择的是朴素的方法,只有当矩阵变稠密,而且矩阵的阶数很大时,才会考虑使用Strassen算法。
看到分治法上面的求最大子数组,下午搞了3个小时,才算是把这个算法搞懂,总结下思路。
分治法的精髓就是:
1、分--将问题分解为规模更小的子问题;
2、治--将这些规模更小的子问题逐个击破;
3、合--将已解决的子问题合并,最终得出“母”问题的解;
ps:看不懂算法的时候,觉得这说的很扯,看不懂。明白了算法之后,觉得这真的是这个算法的精髓。
先举个小例子:
比如,我们需要计算{1,-2}这两个数组成的最大子数组,很简单,答案是1。
因为数字很少,所以我们一眼就能看出来,但是,如果用分治法的思想来求解这个问题,需要以下三步:
1、分:将数组分为1和-2两个元素,分的方法就是取中间位置的元素下标(low-0,mid((low+high)/2)-1,high-1),这里就是(0,0)(1,1)。
2、治:在(0,0)之间最大的元素(只有一个元素)是1,(1,1)最大的元素就是-2。两个相比,最大的元素就是1。
3、合:将(0,0)和(1,1)合起来为(0,1),就是1+-2 = -1。将合起来的结果于上面分的结果进行比较,保留最大的值的数组,即1(0,0)
所以,{1,-2}的最大子数组就是(0,0,1)