数据结构与算法——无权最短路径算法的C++实现
对于一个有权图,任意路径中各个边的权重的和,就是加权路径长。
对于一个无权图,任意路径中边的数目,就是无权路径长。
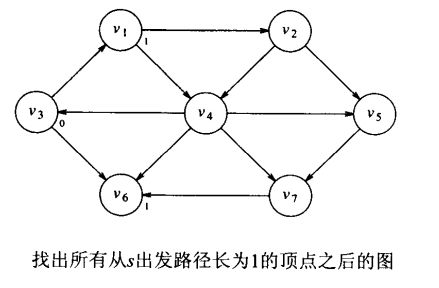
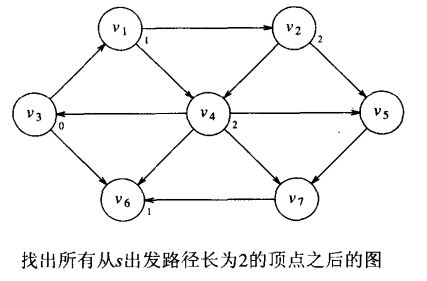
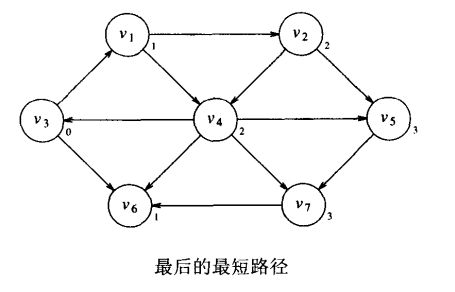
对于上面的无权图G,我们使用某个顶点s作为输入参数,我们想要找出从s到所有其它顶点的最短路径。我们只对路径上边的数目感兴趣,不考虑路径上边的权重(对于无权图可以将权重看为是1)。
算法1详细步骤:
1、选择顶点s为v3。马上可以知道s到v3的最短路径长为0的路径(v3->v3)
这种搜索图的方法称为广度优先搜索。该方法按层处理顶点:距离开始点最近的那些顶点首先被求值,而最远的那些顶点最后被求值。这很像对树的层序遍历。
对于每个顶点,我们将跟踪三个信息。首先,把从s开始到顶点的距离放到dv栏中。开始的时候,除了s外的其它顶点都是不可达的,而到s的路径长为0。pv记录的是该顶点之前的一个顶点。known表示该顶点是否被处理过(确认了距离),初始值都是false,如果确定了s到该顶点的距离,则将known置为true。
保存各个顶点信息的数据结构(也是上面配置表中的结构):
//保存每个顶点信息的数据结构
struct GraphNode{
bool known;//当前顶点距离起点的距离是否确定
int dist;//当前顶点到起点的最短距离
int path;//当前顶点距离起点的最短路径的前一个顶点
};图类的接口:
/*******************************************************
* 类名称: 邻接表图
********************************************************/
class Graph{
private:
int edge_num;//图边的个数
int vertex_num;//图的顶点数目
list * graph_list;//邻接表
vector nodeArr;//保存每个顶点信息的数组
public:
Graph(){}
Graph(char* graph[], int edgenum);
~Graph();
void print();
void unwightedShorestPath(int src);//算法1求最短距离
void unwightedShorestPathAdv(int src);//算法2求最短距离
void printShorestPath(); //输出顶点src到各个顶点最短距离的信息
private:
vector get_graph_value(char* graph[], int columns);
void addEdge(char* graph[], int columns);
}; 关于图邻接表表示法的实现参考: 数据结构与算法——图的邻接表表示法类的C++实现
算法1具体步骤:
1、初始化上面的配置表,known栏全部设为false,
dv
栏全部设置为无穷大,
pv栏初始化为0.
2、先把距离为0上的顶点的dist设为0。
3、从距离currentDist为0开始,遍历每个顶点,如果找到某个顶点的known为false并且该顶点的dv==
currentDist,则将该顶点的known设置为true。然后再遍历所有与该顶点相邻的顶点,如果这些相邻的顶点的dv是无穷大,则将dv设置为currentDist+1,并在这些相邻顶点的pv字段记录该顶点。
4、将currentDist++。重复步骤3,直到currentDist等于顶点的数目。
算法1的函数实现:
/*************************************************
* 函数名称:unwightedShorestPath(int src)
* 功能描述:求无权图的任意点到其它顶点的距离
* 参数列表:src是起点
* 返回结果:void
*************************************************/
void Graph::unwightedShorestPath(int src)
{
//步骤1,初始化配置表
for(int i = 0; i < vertex_num; ++i){
nodeArr[i].known = false;
nodeArr[i].dist = INFINITY;
nodeArr[i].path = 0;
}
//步骤2,先把距离为0的顶点的dist设置为0
nodeArr[src].dist = 0;
//步骤4
for(int currentDist = 0; currentDist < vertex_num; ++currentDist){
//步骤3
for(int i = 0; i < vertex_num; ++i){
if((!nodeArr[i].known) && (nodeArr[i].dist == currentDist)){
nodeArr[i].known = true;
//遍历与顶点i相邻的所有顶点
for(list::iterator it = graph_list[i].begin(); it != graph_list[i].end(); ++it){
if(nodeArr[(*it).vertex].dist == INFINITY){
nodeArr[(*it).vertex].dist = currentDist + 1;
nodeArr[(*it).vertex].path = i;
}
}
}
}
}
}
在算法2中将已经确定了的顶点,还有没有确定的顶点分开。使用了一个队列来实现,放入队列中的都是没有确定的,从队列中弹出的顶点都是已经确定的。
算法2具体步骤:
1、将配置表中各个顶点的dist字段进行初始化为无穷大。
2、将顶点s的dist字段设为0。
3、将顶点s压入队列que中。
4、如果队列que非空,则将队首的元素v弹出。并遍历与v相邻的所有顶点w,如果顶点w的dist为无穷大,则将w.dist设为v.dist+1;w.path=v;并将顶点w压入队列。
5、循环执行步骤4,直至队列que为空。
该算法2没有使用known字段。
算法2函数实现:
/*************************************************
* 函数名称:unwightedShorestPathAdv(int src)
* 功能描述:求无权图的任意点到其它顶点的距离,
* 该算法比unwightedShorestPathAdv要好
* 参数列表:src是起点
* 返回结果:void
*************************************************/
void Graph::unwightedShorestPathAdv(int src)
{
queue que;
//步骤1,将各个顶点的dist设置为无穷大
for(int i = 0; i < vertex_num; ++i)
nodeArr[i].dist = INFINITY;
//步骤2,将顶点src的dist字段设为0
nodeArr[src].dist = 0;
//步骤3,将顶点src压入队列que中
que.push(src);
//步骤5
while(!que.empty()){
//步骤4
int top = que.front();//获得队列的首元素
que.pop();//弹出队列的首元素
//遍历与顶点相邻的所有顶点
for(list::iterator it = graph_list[top].begin(); it != graph_list[top].end(); ++it){
if(nodeArr[(*it).vertex].dist == INFINITY){
nodeArr[(*it).vertex].dist = nodeArr[top].dist + 1;
nodeArr[(*it).vertex].path = top;
que.push((*it).vertex);
}
}
}
} 测试主函数:
int main(int argc, char *argv[])
{
char *topo[5000];
int edge_num;
char *demand;
int demand_num;
char *topo_file = argv[1];
edge_num = read_file(topo, 5000, topo_file);
if (edge_num == 0)
{
printf("Please input valid topo file.\n");
return -1;
}
int src;
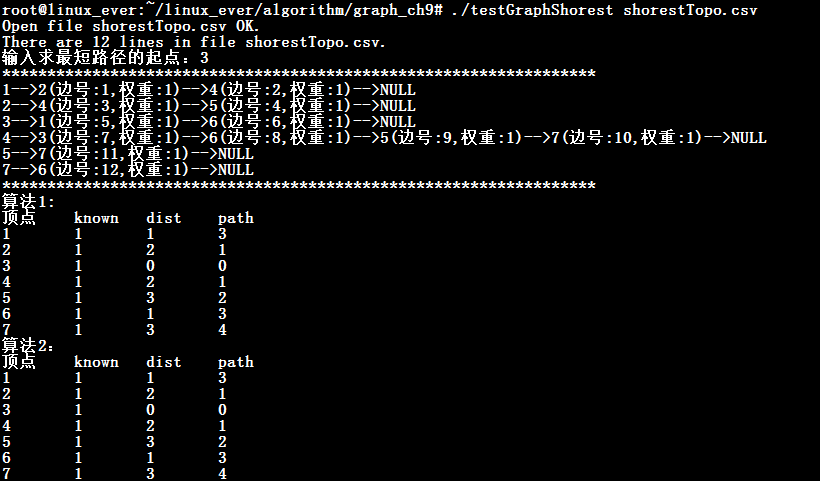
cout << "输入求最短路径的起点:";
cin >> src;
Graph G(topo, edge_num);
G.print();
cout << "算法1: " << endl;
G.unwightedShorestPath(src);
G.printShorestPath();
cout << "算法2:" << endl;
G.unwightedShorestPathAdv(src);
G.printShorestPath();
release_buff(topo, edge_num);
return 0;
}测试的图数据:
1,1,2,1
2,1,4,1
3,2,4,1
4,2,5,1
5,3,1,1
6,3,6,1
7,4,3,1
8,4,6,1
9,4,5,1
10,4,7,1
11,5,7,1
12,7,6,1第1列表示边的编号,第2列表示边的起点,第3列表示边的终点,第4列表示边的权重。因为此时是无权图,所以边的权重为1。
下面是图邻接表类的源代码:
#ifndef GRAPH_H
#define GRAPH_H
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define MAX_VERTEX_NUM 600
#define INFINITY 1000000//将INFINITY定义为无穷大的值
//保存每个顶点信息的数据结构
struct GraphNode{
bool known;//当前顶点距离起点的距离是否确定
int dist;//当前顶点到起点的最短距离
int path;//当前顶点距离起点的最短路径的前一个顶点
};
//图节点信息
typedef struct Node{
int edge_num;//边号
int src;//源点
int vertex;//自身
int weight;//边的权重
}Node;
/*******************************************************
* 类名称: 邻接表图
********************************************************/
class Graph{
private:
int edge_num;//图边的个数
int vertex_num;//图的顶点数目
list * graph_list;//邻接表
vector nodeArr;//保存每个顶点信息的数组
public:
Graph(){}
Graph(char* graph[], int edgenum);
~Graph();
void print();
void unwightedShorestPath(int src);//算法1求最短距离
void unwightedShorestPathAdv(int src);//算法2求最短距离
void printShorestPath(); //输出顶点src到各个顶点最短距离的信息
private:
vector get_graph_value(char* graph[], int columns);
void addEdge(char* graph[], int columns);
};
/*************************************************
* 函数名称:unwightedShorestPathAdv(int src)
* 功能描述:求无权图的任意点到其它顶点的距离,
* 该算法比unwightedShorestPathAdv要好
* 参数列表:src是起点
* 返回结果:void
*************************************************/
void Graph::unwightedShorestPathAdv(int src)
{
queue que;
//步骤1,将各个顶点的dist设置为无穷大
for(int i = 0; i < vertex_num; ++i)
nodeArr[i].dist = INFINITY;
//步骤2,将顶点src的dist字段设为0
nodeArr[src].dist = 0;
//步骤3,将顶点src压入队列que中
que.push(src);
//步骤5
while(!que.empty()){
//步骤4
int top = que.front();//获得队列的首元素
que.pop();//弹出队列的首元素
//遍历与顶点相邻的所有顶点
for(list::iterator it = graph_list[top].begin(); it != graph_list[top].end(); ++it){
if(nodeArr[(*it).vertex].dist == INFINITY){
nodeArr[(*it).vertex].dist = nodeArr[top].dist + 1;
nodeArr[(*it).vertex].path = top;
que.push((*it).vertex);
}
}
}
}
/*************************************************
* 函数名称:unwightedShorestPath(int src)
* 功能描述:求无权图的任意点到其它顶点的距离
* 参数列表:src是起点
* 返回结果:void
*************************************************/
void Graph::unwightedShorestPath(int src)
{
//步骤1,初始化配置表
for(int i = 0; i < vertex_num; ++i){
nodeArr[i].known = false;
nodeArr[i].dist = INFINITY;
nodeArr[i].path = 0;
}
//步骤2,先把距离为0的顶点的dist设置为0
nodeArr[src].dist = 0;
//步骤4
for(int currentDist = 0; currentDist < vertex_num; ++currentDist){
//步骤3
for(int i = 0; i < vertex_num; ++i){
if((!nodeArr[i].known) && (nodeArr[i].dist == currentDist)){
nodeArr[i].known = true;
//遍历与顶点i相邻的所有顶点
for(list::iterator it = graph_list[i].begin(); it != graph_list[i].end(); ++it){
if(nodeArr[(*it).vertex].dist == INFINITY){
nodeArr[(*it).vertex].dist = currentDist + 1;
nodeArr[(*it).vertex].path = i;
}
}
}
}
}
}
/*************************************************
* 函数名称:printShorestPath()
* 功能描述:将获得的src顶点到其它顶点的最短路径输出
* 参数列表:无
* 返回结果:无
*************************************************/
void Graph::printShorestPath()
{
cout << "顶点\t" << "known\t" << "dist\t" << "path" << endl;
for(int i = 0; i < vertex_num; ++i){
if(nodeArr[i].known)
cout << i << "\t" << nodeArr[i].known << "\t" << nodeArr[i].dist << "\t" << nodeArr[i].path << endl;
}
}
/*************************************************
* 函数名称:print
* 功能描述:将图的信息以邻接表的形式输出到标准输出
* 参数列表:无
* 返回结果:无
*************************************************/
void Graph::print()
{
cout << "******************************************************************" << endl;
//for(int i = 0 ; i < MAX_VERTEX_NUM; ++i){
for(int i = 0 ; i < vertex_num; ++i){
if(graph_list[i].begin() != graph_list[i].end()){
cout << i << "-->";
for(list::iterator it = graph_list[i].begin(); it != graph_list[i].end(); ++it){
cout << (*it).vertex << "(边号:" << (*it).edge_num << ",权重:" << (*it).weight << ")-->";
}
cout << "NULL" << endl;
}
}
cout << "******************************************************************" << endl;
}
/*************************************************
* 函数名称:get_graph_value
* 功能描述:将图的每一条边的信息保存到一个数组中
* 参数列表: graph:指向图信息的二维数组
columns:图的第几条边
* 返回结果:无
*************************************************/
vector Graph::get_graph_value(char* graph[], int columns)
{
vector v;
char buff[20];
int i = 0, j = 0, val;
memset(buff, 0, 20);
while((graph[columns][i] != '\n') && (graph[columns][i] != '\0')){
if(graph[columns][i] != ','){
buff[j] = graph[columns][i];
j++;
}
else{
j = 0;
val = atoi(buff);
v.push_back(val);
memset(buff, 0, 20);
}
i++;
}
val = atoi(buff);
v.push_back(val);
return v;
}
/*************************************************
* 函数名称:addEdge
* 功能描述:将图的每一条边的信息加入图的邻接表中
* 参数列表:graph:指向图信息的二维数组
columns:图的第几条边
* 返回结果:无
*************************************************/
void Graph::addEdge(char* graph[], int columns)
{
Node node;
vector v = get_graph_value(graph, columns);
node.edge_num = v[0];
node.src = v[1];
node.vertex = v[2];
node.weight = v[3];
//根据顶点的标号,求的总的顶点数目
if(node.vertex > vertex_num)
vertex_num = node.vertex;
//要考虑重复的边,但是边的权重不一样
for(list::iterator it = graph_list[node.src].begin(); it != graph_list[node.src].end(); ++it){
if((*it).vertex == node.vertex){
if((*it).weight > node.weight){
(*it).weight = node.weight;
}
return;
}
}
graph_list[node.src].push_back(node);
}
/*************************************************
* 函数名称:构造函数
* 功能描述:以邻接表的形式保存图的信息,并保存必须经过的顶点
* 参数列表:graph:指向图信息的二维数组
edgenum:图的边的个数
* 返回结果:无
*************************************************/
Graph::Graph(char* graph[], int edgenum):nodeArr(MAX_VERTEX_NUM)
{
edge_num = edgenum;
vertex_num = 0;
graph_list = new list[MAX_VERTEX_NUM+1];
for(int i = 0; i < edgenum; ++i){
addEdge(graph, i);
}
vertex_num++;
}
/*************************************************
* 函数名称:析构函数
* 功能描述:释放动态分配的内存
* 参数列表:无
* 返回结果:无
*************************************************/
Graph::~Graph()
{
delete[] graph_list;
}
#endif
下面是测试函数的代码:
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include "graphShorestPath.h"
#define MAX_LINE_LEN 4000
int read_file(char ** const buff, const unsigned int spec, const char * const filename);
void release_buff(char ** const buff, const int valid_item_num);
int main(int argc, char *argv[])
{
char *topo[5000];
int edge_num;
char *demand;
int demand_num;
char *topo_file = argv[1];
edge_num = read_file(topo, 5000, topo_file);
if (edge_num == 0)
{
printf("Please input valid topo file.\n");
return -1;
}
int src;
cout << "输入求最短路径的起点:";
cin >> src;
Graph G(topo, edge_num);
G.print();
cout << "算法1: " << endl;
G.unwightedShorestPath(src);
G.printShorestPath();
cout << "算法2:" << endl;
G.unwightedShorestPathAdv(src);
G.printShorestPath();
release_buff(topo, edge_num);
return 0;
}
/****************************************************************
* 函数名称:read_file
* 功能描述: 读取文件中的图的数据信息
* 参数列表: buff是将文件读取的图信息保存到buff指向的二维数组中
* spec是文件中图最大允许的边的个数
* filename是要打开的图文件
* 返回结果:无
*****************************************************************/
int read_file(char ** const buff, const unsigned int spec, const char * const filename)
{
FILE *fp = fopen(filename, "r");
if (fp == NULL)
{
printf("Fail to open file %s, %s.\n", filename, strerror(errno));
return 0;
}
printf("Open file %s OK.\n", filename);
char line[MAX_LINE_LEN + 2];
unsigned int cnt = 0;
while ((cnt < spec) && !feof(fp))
{
line[0] = 0;
fgets(line, MAX_LINE_LEN + 2, fp);
if (line[0] == 0) continue;
buff[cnt] = (char *)malloc(MAX_LINE_LEN + 2);
strncpy(buff[cnt], line, MAX_LINE_LEN + 2 - 1);
buff[cnt][4001] = 0;
cnt++;
}
fclose(fp);
printf("There are %d lines in file %s.\n", cnt, filename);
return cnt;
}
/****************************************************************
* 函数名称:release_buff
* 功能描述: 释放刚才读取的文件中的图的数据信息
* 参数列表: buff是指向文件读取的图信息
* valid_item_num是指图中边的个数
* 返回结果:void
*****************************************************************/
void release_buff(char ** const buff, const int valid_item_num)
{
for (int i = 0; i < valid_item_num; i++)
free(buff[i]);
}