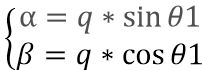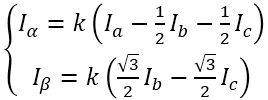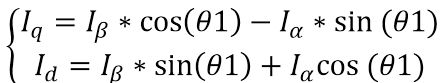电机FOC算法的解释

一、开始说FOC之前，我们先来弄清楚电机是怎么动起来的，电机的q轴、d轴是什么，FOC存在的意义是什么。

这里有一篇知乎的文章，作者w浩森说的太好了，推荐大家去看一看。我这里总结几条本文章后面需要用到的观点：

1、电机的本质，扭矩的本质

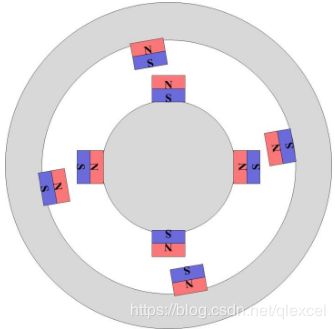
上左图是电机等效模型，现在转子和定子都是完全重合在一起的，不会有扭矩的存在。

上右图，把外面的定子磁场扭转一定角度，根据磁铁异性相吸的原理，内部的转子会跟着旋转，这个时候就存在扭矩了。扭矩的大小怎么衡量呢？

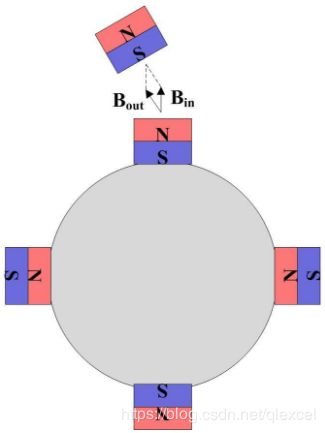
所有的电机，扭矩的大小正比于内外两个磁场的叉乘，也就是两个磁场围成的平行四边形的面积。于是当两个磁场重合，平行四边形面积为0，此时扭矩为0。当两个磁场呈90度，平行四边形面积最大，扭矩也最大。

2、由两个磁场的叉乘引出电机的d轴和q轴的概念

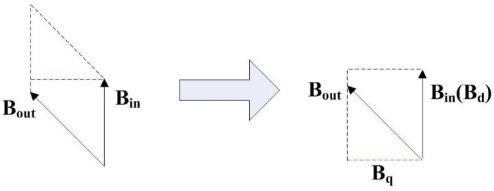
        把上面的两个磁场叉乘的平行四边形重新组合成一个矩形，组合前后面积不变。这个时候扭矩的大小就可以用平行于内磁场的磁场大小（我们称为d轴，direct，也称直轴。其大小等于内磁场+外磁场在内磁场方向上的分量）乘上垂直于内磁场的大小（我们称为q轴，quadrature，也称交轴。其大小等于外磁场在内磁场垂直方向上的分量）。

        现在对于电机扭矩大小的控制就变成了q轴和d轴大小乘积的控制。在PMSM中，内磁场的大小是永磁铁产生的，是恒定的。外磁场是由线圈绕组产生的，外磁场与内磁场之间的夹角和外磁场的大小，都可以被控制。比如：例1、假设内磁场在0度，大小为1，我们可以控制电机绕组产生超前于内磁场45度的外磁场，大小为2，则总的扭矩大小为1*2*sin(45)。例2、假设内磁场在0度，大小为1，我们控制电机绕组产生超前于内磁场90度的外磁场，大小为2，则总的扭矩大小为1*2*sin(90)。可知当内外两个磁场方向垂直时，外磁场产生相同大小磁场，得到的扭矩最大。也就是下面这种样子：

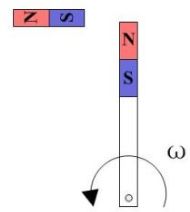
        在d轴上面施加磁场只能影响转子的磁场，并不能得到扭矩。因此我们说：d轴控制转子磁通，q轴控制电机的转矩输出，一般的使用中我们只需要控制电机的转矩输出即可，可以直接把d轴设置为0。

3、反park变换

        我们能控制的因素其实只有：1、外磁场在d、q轴上的大小。2、外磁场的角度。

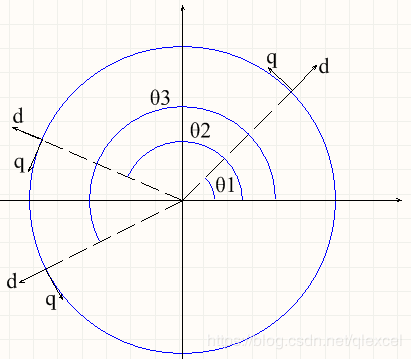
        我们要做的事情其实只是：用编码器测量转子的电角度，然后根据转子的电角度（内磁场的角度）用电机绕组产生设置了d、q轴大小的外磁场。

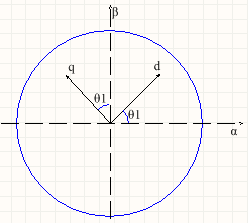
        如上图所示，如果转子的电角度在θ1，则我们就要在θ1处产生d、q轴大小的外磁场。如果转子的电角度在θ2，则我们就要在θ2处产生d、q轴大小的外磁场。好了，现在我们引入第一个变换：反park变换（你也许会问，为什么要变换呢？这个就跟式子化简或者变形金刚变形一样，变过去又可以变回来，不过你可能会发现，明明都是一样的东西，变个形态，怎么问题就变得这么简单）

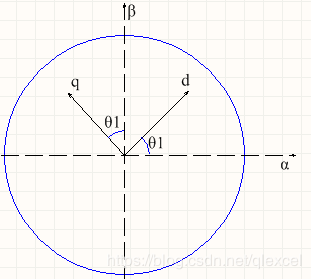
        我们把角度θ1的情况单独提出来，把它移到原点去，然后把x、y轴重命名为α,β：

根据空间矢量的关系，我们可以把q、d轴的大小分解到α,β轴上：

如果d轴等于0：

上面这个式子的意义是：互差90度的大小随正弦规律变化的两个磁场，可以产生大小恒定的旋转磁场。

（此处差一个gif图。。。）

有没有发现分解到α,β轴上的式子其实就是svpwm算法的输入？详情看这儿SVPWM算法原理及详解

        行了，怎么控制电机已经说完了，总结一下：控制PMSM只需要4步：第一步，选定q、d轴的值（比如q=2，d=0）。第二步，用编码器测量转子电角度。第三步，用上面的式子计算α,β值。第四步，把α,β输入SVPWM。

        到这里我们已经用上面的4个步骤让电机转起来了，可是还存在几个问题：1、我怎么知道电机有没有按照我设定的q、d值来转呢？2、设定q、d值只能控制扭矩，我如果要控制电机的速度和位置怎么办？这些问题都是上面那个开环系统解决不了的，这个时候就要引入闭环了。

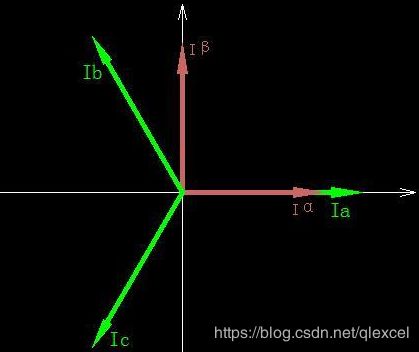
4、clark变换

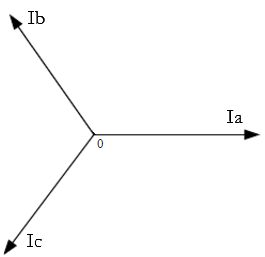
        我们先测量电机的3相电流，但是从SVPWM知道，电机的3相电流是这样的：

是互差120度的三个分磁场，但是我们只需要互差90度的两个磁场。于是又要用一个变换，把3个分磁场变换成两个分磁场：

公式就是矢量分解：

变换中有一个系数k，一般取2/3，有兴趣可以去这儿了解：https://blog.csdn.net/daidi1989/article/details/89926324

5、park变换

再把α,β轴上值通过反park变换的逆过程，park变换，得到q、d轴的值。

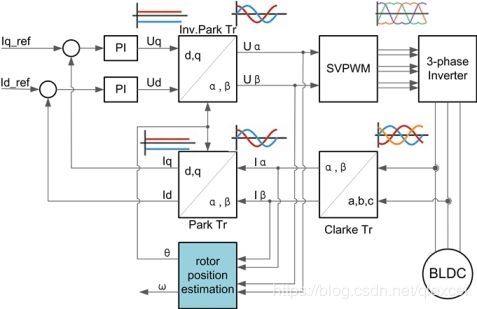
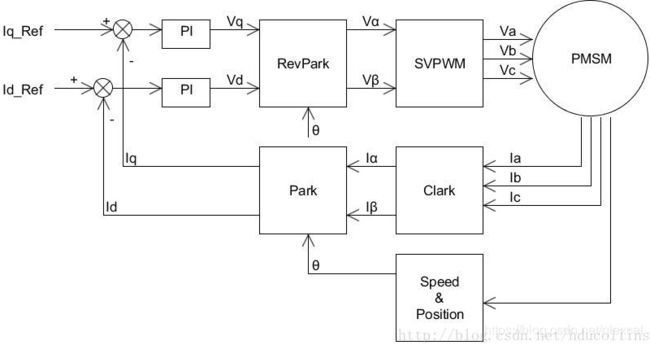
6、现在我们就实现了FOC的整个过程，框图如下：

1、测量q、d轴的值：测量电机的相电流（测量两相，通过Ia+Ib+Ic=0得到第三相），然后通过clark变换得到Iα和Iβ,然后通过park变换得到q、d轴的值。

2、把测量到的d、q轴值与我们设定的做对比，如果大了要减小，小了要增大。（目标是让测量值与我们的设定值相同）

3、通过PID后的控制结果输出给SVPWM执行。

例如：1、设定q=2、d=0，通过测量得到q=1.5、d=0.5，这个时候就有误差了，于是把误差值输入PID，得到PID计算之后的消除误差的控制值，这个控制值还是q、d轴的值，再经过反park变换得到α,β，输出给SVPWM，这就完成了一个控制环路，这个控制环路的目的就是让测量到的q、d值等于他们的设定值，控制q、d值其实就是控制电流值，于是这个环路就叫电流环。

2、设定电机转速2000RPM，通过测量得到当前转速1000，于是要加快旋转。怎么加快旋转呢？我们只能控制q、d这两个值，当然是增大q轴的值，加大扭矩咯。于是改变q轴的设定值，之前是2，现在改为3。电机的速度快起来了，可是超过了2000，于是又要把q轴的设定值减小。这个环路就是速度环，即在电流环的外面加一层，速度环通过改变q、d设定值来改变速度。

3、当然还有位置环，计算位置误差，计算参考速度，然后输出给速度环。

 

部分图片来自：https://blog.csdn.net/u010671230/article/details/79478582，侵删。